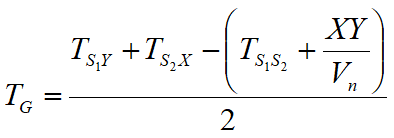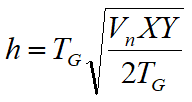La prospección por refracción sísmica permite interpretar la estratigrafía del subsuelo gracias al uso del principio físico del fenómeno de la refracción total de una onda sísmica que incide sobre una interfase localizada entre dos cuerpos con diferentes propiedades mecánicas, (horizonte de refracción). La condición fundamental para llevar a cabo estudios de sísmica por refracción es que la sucesión de los estratos a investigar se caracterice por velocidades sísmicas crecientes al aumentar la profundidad. De este modo se pueden evaluar hasta 4 ó 5 horizontes de refracción diferentes.
Los ensayos se basan en la medición de los tiempos de recorrido de las ondas elásticas para las cuales -suponiendo amplias superficies de separación con respecto a la longitud de onda o en todo caso con una débil curvatura- los frentes de onda se representan por medio de los relativos rayos sísmicos. El análisis se basa en el principio de Fermat y en la ley de Snell.
El principio de Fermat establece que el rayo sísmico recorre la distancia entre la fuente y el receptor siguiendo el trayecto para el cual el tiempo empleado de recorrido es mínimo. En este principio, dado un plano que separa dos medios con diferentes características mecánicas, el rayo sísmico es el que se extiende a lo largo de un plano perpendicular a la interfase que contiene tanto la fuente como el recibidor.
La ley de Snell es una fórmula que describe los tipos de refracción de un rayo sísmico en la transición entre dos medios caracterizados por diferentes velocidades de propagación de las ondas o, equivalentemente, por diferentes índices de refracción. El ángulo formado entre la interfase y el rayo se denomina ángulo de incidencia θi, mientras que el formado entre el rayo refractado y la superficie normal se denomina ángulo de refracción θr. La fórmula matemática es:
|
|
(1) |
Donde v1 e v2 son las velocidades de los dos medios separados por la interfase.
Cuando v1 > v2 se tiene que θi > θr y por lo tanto la sísmica por refracción nos es factible ya que el rayo refractado se inclinaría hacia abajo. Cuando v1<v2 se tiene que θi < θr y existe un ángulo crítico de incidencia por lo que θr = 90° y el rayo refractado viaja paralelamente a la interfase. La expresión que define el ángulo crítico e:
|
|
(2) |
La forma más sencilla de analizar los datos de refracción es construyendo un gráfico tiempo-distancia cuyo origen corresponda a la fuente de generación de las ondas elásticas. En el eje de las abscisas se representan las posiciones de los geófonos y en las ordenadas los tiempos de primera llegada. A los geófonos más cercanos a la fuente llegan primero los impulsos que han seguido el recorrido directo en un tiempo T dado por la relación
|
|
(3) |
Donde xi es la distancia entre el punto de disparo y el punto de detección.
La ecuación (3) una recta que pasa por el origen de los ejes tiempos-distancias y su coeficiente angular permite calcular la velocidad V1 del primer medio como
|
|
(4) |
Los tiempos de llegada de los rayos refractados en el diagrama tiempos-distancias se disponen según una recta que tendrá una inclinación menor a la de las ondas directas.

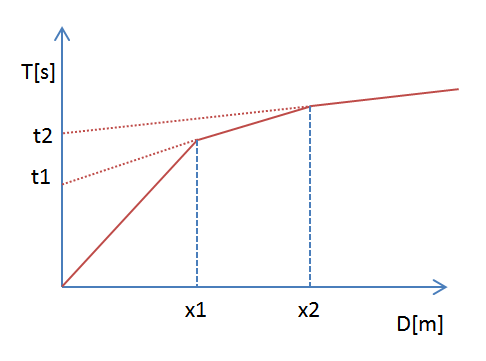
La curva tiempos-distancias tiende a un comportamiento regular según una polilínea cuyos vértices se denominan codos, los cuales representan, físicamente, la condición donde se da la llegada contemporánea de las ondas directas y la refractadas. Por lo tanto para cada uno de los segmentos se determina el tiempo de retraso ti que representa la diferencia entre el tiempo que el rayo sísmico emplea en recorrer un tramo a la velocidad propia del estrato en el cual se transmite y el tiempo que emplearía para viajar a lo largo del componente horizontal de ese tramo a la máxima velocidad alcanzada en toda la trayectoria de refracción.
Gráficamente el tiempo de retraso está dado por la intersección de la recta que comprende un segmento de la curva tiempo-distancia con el eje de los tiempos.
Entonces, conociendo los tiempos ti es posible obtener los espesores de los refractores mediante la relación:
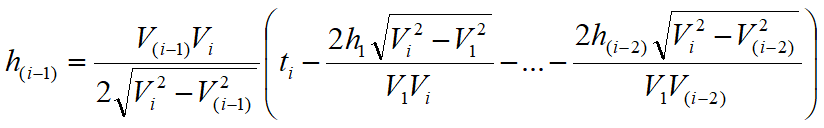 (5)
(5)
En situaciones morfológicamente complejas, como método de elaboración se puede utilizar el Método de reciprocidad generalizada (Generalized Reciprocal Method) examinado por Palmer en 1980.
Este método se basa en la búsqueda de una distancia virtual XY entre geófonos tal que los rayos sísmicos que parten de puntos de disparo simétricos respecto al tendido, lleguen al geófono colocado en la posición X y al colocado en la posición Y, proviniendo desde un mismo punto del refractor.
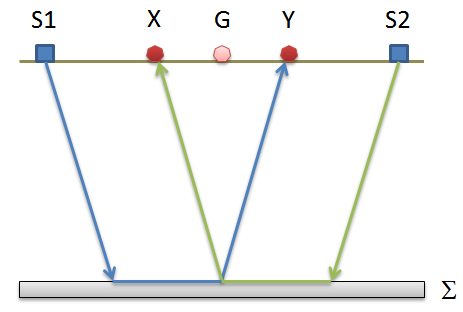
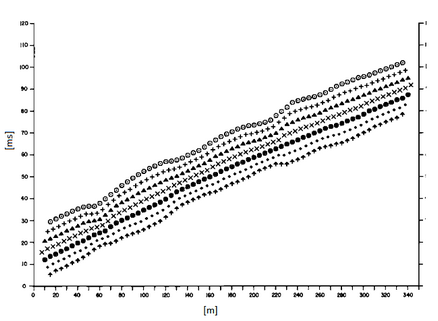
El primer paso operativo es construir un diagrama tiempos-distancias identificando en los sismogramas obtenidos con los datos de campo, las primeras llegadas de las ondas sísmicas. Para determinar la distancia óptima XY es necesario considerar varios puntos de disparo, tanto de los extremos como del interior del tendido. Esto hace posible identificar con más precisión los tiempos relativos de un mismo refractor que sirven para caracterizar las dromocronas, las cuales son fundamentales para la interpretación. En las interpretaciones multi estratos, para generar las dromocronas se puede aprovechar las técnicas de phantoming y así superar la falta de datos de algunos refractores.
Partiendo de la construcción de las dromocronas es posible determinar la función velocidad según la ecuación
Donde TS1Y y TS2X son los tiempos de recorrido de los rayos sísmicos para llegar, respectivamente, de la fuente S1 a X y de la fuente S2 a Y, mientras que TS1S2 es el tiempo de recorrido entre dos puntos de disparo S1 y S2, externamente simétricos con respecto al tendido. Tv es el tiempo calculado en un geófono G puesto entre X y Y, no necesariamente coincidente con la posición de un geófono del tendido.
El cálculo de la función Tv se lleva a cabo para cada valor de XY comprendido entre cero y la mitad del tendido con variación igual a la distancia real entre los geófonos del tendido. La mejor recta de regresión de las funciones de velocidad obtenidas, permite determinar el XY óptimo y la velocidad del refractor que se obtiene del coeficiente angular.
Mediante la función tiempo-profundidad es posible encontrar la profundidad del refractor expresada en unidad de tiempo. Dicha función se expresa con:
Donde Vn es la velocidad del refractor.

De la misma manera que con la función velocidad, se determinan varias funciones tiempo-profundidad para el conjunto de los valores XY en estudio. Entre las funciones encontradas, la que presente la mayor articulación compete al valor óptimo de XY.
Finalmente, es posible determinar el espesor del refractor en las correspondientes posiciones de los geófonos G mediante la relación:
|
|
(8) |
h representa la profundidad mínima desde el geófono G por lo tanto la morfología del refractor se define con la envolvente de las semicircunferencias de rayo h.
Una de las principales ventajas del G.R.M. es que el factor de conversión de la profundidad es relativamente insensible a las pendientes hasta aproximadamente 20°
© Geostru