Le NTC 2018 consentono che il calcolo della resistenza di progetto possa essere effettuato sia con procedimenti analitici che sulla base di prove di carico statico di progetto su pali pilota.
In ogni caso, in corso d'opera, devono essere eseguite prove di carico statico fino ad un valore del carico pari a 1,5 volte l'azione di progetto allo SLE.
Sia nel caso delle prove di progetto su pali pilota che su quelle in corso d'opera è quasi sempre possibile assimilare il comportamento non lineare della curva carichi-cedimenti ad una iperbole avente parametri m, n deducibili dai dati rilevati durante le prove. Il calcolo statistico di tali parametri consente sia la derivazione (eventualmente anche per estrapolazione) del carico limite del palo, sia l'impiego dell'iperbole nel calcolo non lineare dei cedimenti di una palificata comunque collegata (plinti, platea, graticcio di travi).
Sono previsti i seguenti due specifici sottoprogrammi per il calcolo della resistenza assiale del palo singolo:
- Calcolo della resistenza assiale basato su prove di carico su pali pilota.
- Calcolo analitico della resistenza assiale di un palo trivellato
Il calcolo può riguardare prove di carico su:
- Pali trivellati
- Pali ad elica continua
- Pali infissi
E' anche prevista l'importazione dei punti Carico-Cedimento (per uno o più pali di prova) rilevati in sede di prova. In questo caso va predisposto un file di testo (*.txt) avente la seguente struttura di dati:
<Breve riga di descrizione della prova>
<Numero di pali provati>
<Numero di punti letti sulla prima curva carichi cedimenti>
<Carico Q [MN], cedimento w [mm]>
<... , ...>
<Carico Q [MN], cedimento w [mm]>
I carichi vanno separati dai cedimenti da una virgola. I cedimenti vanno sempre espressi in mm ed i carichi in MN. [1MN = 100000 daN = 1000 kN]
Di seguito un esempio di file riferito ad un'unica prova di carico in cui:
La prima riga è una stringa che descrive la prova
La seconda riga è il numero di prove eseguite
La terza riga è il numero M1 di misure eseguite nella prova n. 1
Le successive M1 righe devono contenere (separate da virgola) le coppie di misure (Q, w) eseguite
La successiva riga è il numero M2 di misure eseguite nella seconda prova (se eseguita)
e così via. Ad esempio:
Rodi- Prova collaudo palo 34 d=60 cm
1
6
0.437,0.19
0.875,0.59
1.312,1.03
1.750,1.65
2.187,2.26
2.625,2.95
Viene utilizzata la tecnica di interpolazione iperbolica per cui la curva carico-cedimento viene interpolata con l'equazione delliperbole w/Q = m + n w. I parametri m e n dell'iperbole vengono calcolati mediante elaborazione statistica e rappresentano i due parametri della retta interpolatrice nel piano w-Qw di rappresentazione dell'iperbole.
Migliore è l'approssimazione di tale retta con i punti misurati maggiore è la vicinanza ad 1 del parametro statistico R² (pari al rapporto tra la devianza di regressione e la devianza totale). Cioè se R² è molto vicino ad 1 la curva carico-cedimento è molto ben approssimata dall'iperbole con parametri m, n.
Il carico Q di rottura viene stimato tramite l'eq. dell'iperbole ponendo w pari al cedimento minimo di normativa (0.1 D per pali con D<80 cm e 0.05 per pali con diametro superiore.
Il Carico resistente di progetto del palo viene infine valutato in base alle relazioni di cui al §6.4.3.1.1 NTC a partire dai carichi ultimi medi e minimo, passando per la resistenza caratteristica.Una volta calcolata la resistenza assiale di progetto del palo ed i parametri m, n dell'iperbole è possibile inserire tali dati nel calcolo non lineare di una struttura di fondazione allo scopo di meglio valutare i cedimenti della palificata anche in presenza di platea elastica collaborante (Fondazione mista).
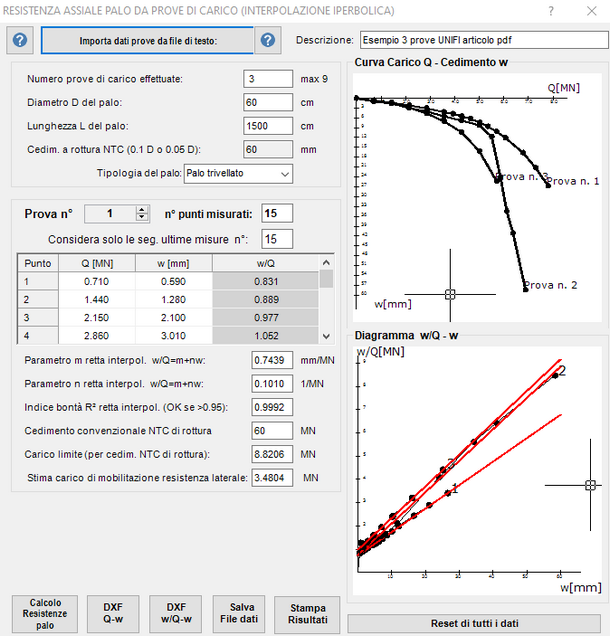
L'esempio in figura (tratto da un documento della sezione Geotecnica dell'Università di Firenze a firma di J.Facciorusso, C.Madiai, G.Vannucchi) si riferisce a n. 3 prove di carico su pali pilota (i relativi files di testo sono presenti nella cartella \ESEMPI.F3F\Prove_di_carico_F3F con la denominazione prova_palo.txt, prova_palo2.txt, prova_palo3.txt . Nel grafico w-w/Q si può valutare, per ogni curva di carico, il suo grado di avvicinamento al comportamento iperbolico dalla vicinanza dei punti di prova alla retta interpolatrice del comportamento iperbolico.
Viene infine stimata la resistenza laterale del palo tramite la formula: Qlat=1/n(1-sqr(mEA/L).
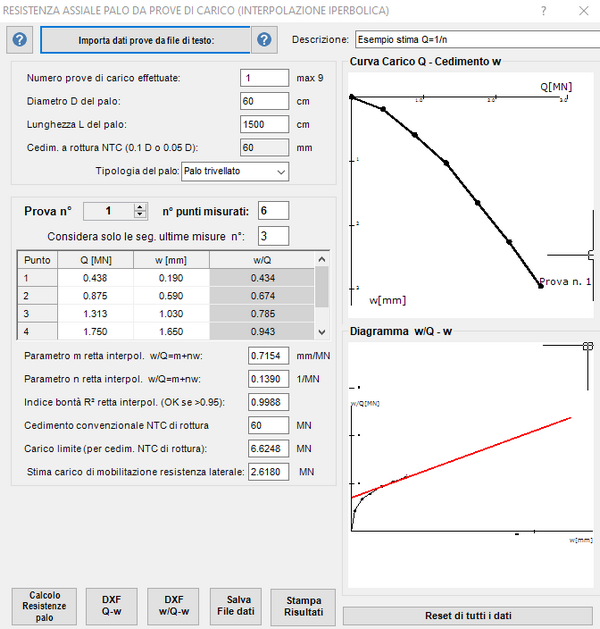
Il caso qui sopra riportato è quello di una prova di carico in cui non si è raggiunto il cedimento minimo di rottura (ad es. prove in corso d'opera o di collaudo). E' possibile ricorrere all'estrapolazione dell'iperbole utilizzando, in questo caso, solo gli ultimi 3 punti misurati in quanto marcatamente non lineari. La retta che interpola i dati ha coeff. angolare n= 0.1389 ed intercetta m= 0.7168. In questo caso il carico di rottura viene stimato con l'espressione Q = 0.9 / n = 6.47 MN. (cfr. Volume FONDAZIONI- C.Viggiani). Di seguito la stampa dettagliata dei risultati:
CALCOLO RESISTENZA ASSIALE PALO DA PROVE DI CARICO COL METODO DELL'IPERBOLE DI CHIN
Esempio 3 prove UNIFI articolo pdf
Numero di prove eseguite: 3
Diametro D del palo: 80 cm
Lunghezza L del Palo: 2350 cm
Tipologia del Palo: Trivellato
Cedimento minimo a rottura: 80 mm Vale 0.1 D per D < 80 cm e 0.05 per D >=80 cm (§6.4.3.7.1 NTC)
Misure Carichi Q-Cedimenti w Palo n° 1 (Numero misure = 15)
Q [MN] w [mm] w/Q [mm/MN]
0.710 0.59 0.831
1.440 1.28 0.889
2.150 2.10 0.977
2.860 3.01 1.052
3.570 4.15 1.162
3.930 4.71 1.198
4.280 5.38 1.257
4.640 6.16 1.328
5.020 7.33 1.460
5.350 8.55 1.598
5.710 10.10 1.769
6.070 12.01 1.979
6.780 16.55 2.441
7.290 21.08 2.892
7.800 26.63 3.414
Parametro m iperbole: 0.7439 mm/MN Coeff. m eq. iperbole: Q = w/(m+nw) (Intercetta retta su asse w/Q)
Parametro n iperbole: 0.7439 1/MN Coeff. n eq. iperbole: Q = w/(m+nw) (Coeff. angolare retta interpol.)
Parametro statistico R²: 0.9992 Indice di coincidenza dell'iperbole con la curva Q-w (OK se R²>0.95)
Misure Carichi Q-Cedimenti w Palo n° 2 (Numero misure = 15)
Q [MN] w [mm] w/Q [mm/MN]
0.714 0.61 0.854
1.428 1.47 1.029
2.141 2.89 1.350
2.855 3.89 1.362
3.569 5.43 1.523
4.283 6.73 1.570
4.997 8.14 1.629
5.506 11.68 2.121
5.863 24.02 4.096
6.118 34.38 5.619
6.373 41.01 6.435
6.883 58.33 8.474
Parametro m iperbole: 0.7716 mm/MN Coeff. m eq. iperbole: Q = w/(m+nw) (Intercetta retta su asse w/Q)
Parametro n iperbole: 0.7716 1/MN Coeff. n eq. iperbole: Q = w/(m+nw) (Coeff. angolare retta interpol.)
Parametro statistico R²: 0.9963 Indice di coincidenza dell'iperbole con la curva Q-w (OK se R²>0.95)
Misure Carichi Q-Cedimenti w Palo n° 3 (Numero misure = 15)
Q [MN] w [mm] w/Q [mm/MN]
0.710 0.90 1.268
1.430 1.56 1.091
2.140 2.76 1.290
2.860 4.57 1.598
3.570 6.98 1.955
4.280 10.29 2.404
5.000 16.04 3.208
5.710 25.25 4.422
Parametro m iperbole: 0.9869 mm/MN Coeff. m eq. iperbole: Q = w/(m+nw) (Intercetta retta su asse w/Q)
Parametro n iperbole: 0.9869 1/MN Coeff. n eq. iperbole: Q = w/(m+nw) (Coeff. angolare retta interpol.)
Parametro statistico R²: 0.9953 Indice di coincidenza dell'iperbole con la curva Q-w (OK se R²>0.95)
CALCOLO RESISTENZE PALO
Viene utilizzata la tecnica di interpolazione iperbolica per cui la curva carico-cedimento viene interpolata con l'equazione delliperbole
w/Q = m + n w. I parametri m e n dell'iperbole vengono calcolati mediante elaborazione statistica e rappresentano i due parametri della
retta interpolatrice nel piano w-Qw di rappresentazione dell'iperbole.
Migliore è l'approssimazione di tale retta con i punti misurati maggiore è la vicinanza ad 1 del parametro statistico R².
Cioè se R² è molto vicino ad 1 la curva carico-cedimento è molto ben approssimata dall'iperbole con parametri m, n. Il carico Q di rottura
viene stimato tramite l'eq. dell'iperbole ponendo w pari al cedimento limite di normativa (0.1 D per pali con D<80 cm e 0.05 per pali con
diametro superiore. Nel caso di prove di carico in cui non si raggiunga il cedimento limite di rottura (ad es. prove in corso d'opera o di
collaudo) è possibile ricorrere all'estrapolazione dell'iperbole utilizzando solo gli ultimi punti misurati in quanto marcatamente non lineari.
In questo caso il carico di rottura viene calcolato con l'espressione Q = 0.9 / n. (cfr. Volume FONDAZIONI- C.Viggiani).
Viene infine stimata la sola resistenza laterale del palo tramite la formula: Qlat=1/n(1-sqr(mEA/L).
Resistenza rott. prova n. 1: 9.069 MN Valutata per cedimento w pari al quello limite di normativa
Resistenza rott. prova n. 2: 6.914 MN Valutata per cedimento w pari al quello limite di normativa
Resistenza rott. prova n. 3: 6.712 MN Valutata per cedimento w pari al quello limite di normativa
Resistenza media 7.565 MN
Resistenza minima 6.712 MN
Fatt. correl. della media 1.20 Tabella 6.4.III NTC 2018
Fatt. correl. del minimo 1.05 Tabella 6.4.III NTC 2018
Resistenza caratteristica Rk 6.304 [6.4.1] NTC 2018
Resistenza di progetto Rd 4.849 Coeff. parziale R3 = 1.30
|
© GeoStru Software