Il calcolo dei cedimenti immediati viene svolto con riferimento al modello di Koenig e Sherif, cioè applicando la teoria dell'elasticità (Boussinesque) ma riferendola ai soli strati di terreno compresi entro una profondità (sotto il piano di posa delle fondazioni) pari, circa, alla dimensione B del plinto (o della platea se molto rigida) o pari a 2 volte, circa, la dimensione B trasversale della trave di fondazione (cfr. § 9.6 Viggiani [7]). Pertanto la somma degli spessori H da assegnare nella griglia di Input deve essere circa pari alle suddette profondità. Nel caso di fondazioni miste lo spessore deve essere maggiore, oltre che alla dimensione trasversale B della platea, anche della lunghezza dei pali fino a considerare la profondità significativa dal punto di vista geotecnico.
Se si conoscono i moduli edometrici M0 degli strati di terreno coesivo è possibile stimare anche i cedimenti di consolidazione.
Il programma prevede la discretizzazione della pianta della fondazione a partire dalla Mesh assegnata (se il numero di elementi discreti supera il valore di 1000 la dimensione della mesh viene automaticamente incrementata). Calcolate per ogni rettangolo discreto le aree (tutte uguali), le coordinate dei baricentri e la risultante delle pressioni che su di esso insistono, viene costruita la matrice di deformabilità del terreno mediante i coeff. riportati nel capitolo 4 del volume [19]. Per tener conto dello spessore finito dei singoli strati di terreno considerati dette relazioni vengono modificate in base all'approssimazione di Streinbrenner (vedi volume citato).
Nel caso di fondazione (infinitamente) flessibile: nota la matrice di deformabilità ed i singoli carichi agenti sugli elementi è immediata (cioè senza la risoluzione di un sistema di equazioni) la valutazione dei cedimenti dei baricentri singoli elementi discreti.
Nel caso di fondazione (infinitamente) rigida: viene invertita la matrice di deformabilità ottenendo la matrice di rigidezza del terreno. Detta matrice viene condensata in una matrice 3x3 corrispondente alle sole 3 deformazioni della fondazione (cedimento verticale, rotazione intorno all'asse X e rotazione intorno all'asse Y). Assumendo come termini noti del sistema 3x3 gli sforzi totali assegnati in input N, Mx, My, la risoluzione del sistema conduce alle deformazioni del piano rigido di contattto fondazione-terreno.
Per le sole fondazioni flessibili il programma calcola, negli 8 punti principali della fondazione, il cedimento a lungo termine sulla base dei moduli edometrici Mo da assegnare ai vari strati del terreno sulla base delle prove eseguite. Anche se detti valori si riferiscono a fondazioni flessibili possono essere assunti a favore di sicurezza anche per le fondazioni reali dotate di rigidezza flessionale (mai infinitamente rigide) che può in effetti variare da caso a caso. Per fondazioni rigide si può indicare un cedimento medio fornito dal calcolo edometrico nel caso di fondazioni rettangolari (Poulos): w = 0.33 ( 2 ⋅ wcentro + wspigolo)
Per platee su argilla il cedimento ammissibile SLE può assumersi pari a wmax [mm] = 30000 ⋅ βmax in cui βmax è la rotazione relativa massima βmax che, per telai in ca con tompagni, può assumrsi pari a βmax=1/500. Per platee su sabbia può assumersi pari a wmax [mm] = 18000 ⋅ βmax . Nel caso di collegamento a servizi wmax= 65 mm.
Se i momenti flettenti assegnati comportano il distacco anche parziale (per sollevamento) della fondazione è opportuno modificare le dimensioni della fondazione (il calcolo viene interrotto).
Naturalmente gli spessori degli strati ed i parametri meccanici del terreno E, µ, Mo vanno assunti sulla base delle indagini geotecniche eseguite. Nel caso di terreni con incremento sensibile del modulo E con la profondità (argille sovraconsolidate o terreni sabbiosi) lo spessore H dello strato può essere suddiviso in più strati con valori crescenti di E.
Esempio
Si considera la platea quadrata di lato B=L=1000 cm e spessore H=150 cm rappresentata in figura. Il terreno è costituito da argilla satura di media consistenza fino alla profondità di 30 metri. I dati geotecnici relativi al suddetto strato sono i seguenti:
Cu = 0.07 M/mm²
E = 32.0 N/mm² modulo elastico terreno ricavato da prove geofisiche
Mo = 8.0 N/mm² modulo edometrico costante per tutto lo strato ricavato da prove CPT
Il cedimento SLE massimo ammissibile viene calcolato assumendo una rotazione relativa massima pari a βmax = 500, da cui si ricava, per terreno argilloso, un cedimento ammissibile: wmax = 30000 / 500 = 60 mm = 6.0 cm.
La platea risulta già verificata nei confronti degli SLU. Si vuole ora effettuare la verifica dei cedimenti (immediati e a lungo termine) allo SLE e stimare un valore per il coeff. Kw di sottofondo (da assegnare successivamente alla struttura di fondazione con i suoi carichi applicati concentrati e distribuiti nelle loro precise posizioni) che tenga conto di tali cedimenti.
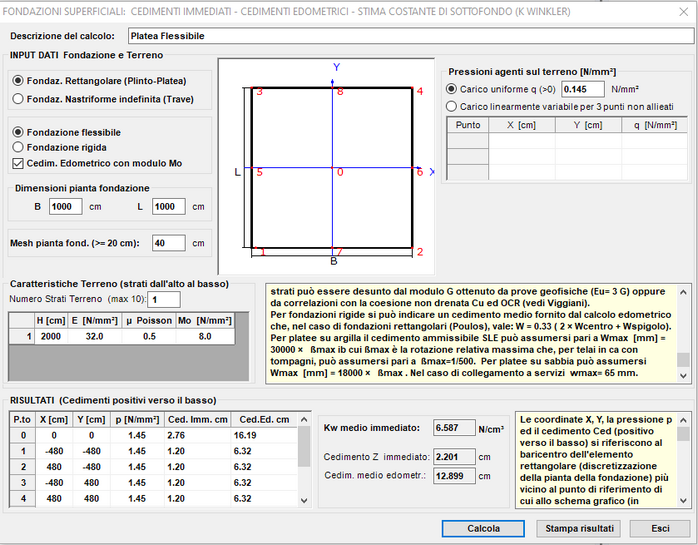
Il carico SLE di progetto complessivo e centrato gravante sul terreno sotto la platea è pari a Ed(SLE)= 20300 kN che corrisponde ad una pressione uniforme q(SLE) = 0.145 N/mm² assegnata in figura (nel caso di carico distribuito eccentrico è possibile assegnare in programma 3 valori di q per definire un generico piano di carico inclinato).
Inseriti in griglia i dati geotecnici assegnati ed una profondità di 2000 cm entro cui valutare le deformazioni nell'unico strato di terreno qui previsto, si ottengono i risultati esposti in figura. Mentre il cedimento medio immediato (cm 2.2) non crea problemi, quello edometrico (sia pure condiderando quello che tiene conto di una certa rigidezza della platea secondo la formula empirica di Poulos prima specificata) pari a 12.9 cm risulta molto più grande di quello massimo ammissibile di 6.0 cm.
Il coeff. di sottofondo da attribuire al cedimento a lungo termine può essere quindi valutato come rapporto tra la pressione unitaria media ed il cedimento medio a lungo termine: Kw= 14.5/12.9 = 1.124 N/cm³
S.L.E. - Calcolo cedimenti elastici immediati ed edometrici. Stima coeff. sottofondo (Kwinkler)
Descrizione del calcolo: Platea Flessibile
Tipologia fondazione: Rettangolare
Tipologia fondazione: Fond. flessibile rigidezza nulla della fondazione nel calcolo di deformazione
Larghezza B fond.: 1000 cm
Lunghezza L fond.: 1000 cm
Carico q: 0.145 N/mm² carico unitario uniforme trasmesso dalla fondazione al terreno
Caratteristiche del terreno:
STRATO N°: 1
Spessore strato: 2000 cm
Modulo elastico E: 32.0 N/mm²
Coeff. di Poisson µ: 0.50
Modulo edometrico Mo: 8.0 N/mm²
Risultati riferiti ai punti significativi della fondazione rettangolare
Punto n° Oltre al baricentro della fondazione (punto 0) il calcolo è rifertito ad altri 8 punti
_ _ (i 4 spigoli e i 4 punti medi dei lati). Detti punti corrispondono ai baricentri
_ _ degli elementi, generati dalla discretizzazione, più vicini ai punti stessi.
X cm Ascissa punti significativi (assi riferim. baricentrico)
Y cm Ordinata punti significativi (assi riferim. baricentrico)
p N/mm² pressione di contatto fond.-terreno in corrisp. dei punti
Ced.Ist. cm cedimenti immediati dei punti significativi della fondazione.
Ced.Ed. cm cedimenti edometrici dei punti significativi della fondazione.
Punto X Y p Ced.Ist. Ced.Ed. Note
0 0 0 1.45 2.76 16.19 Baricentro della fondazione
1 -480 -480 1.45 1.20 6.32 Spigolo inf. sin. fondazione
2 480 -480 1.45 1.20 6.32 Spigolo inf. des. fondazione
3 -480 480 1.45 1.20 6.32 Spigolo sup. sin. fondazione
4 480 480 1.45 1.20 6.32 Spigolo sup. des. fondazione
5 -480 0 1.45 1.79 9.88 Punto medio lato sin. fondazione
6 480 0 1.45 1.79 9.88 Punto medio lato des. fondazione
7 0 -480 1.45 1.79 9.88 Punto medio lato inf. fondazione
8 0 480 1.45 1.79 9.88 Punto medio lato sup. fondazione
Kw medio immediato (press. media/cedim. medio) = 6.6 N/cm³
Cedimento medio immediato = 2.20 cm
Cedimento medio edometr.: 12.90 cm
N.B. Il calcolo dei cedimenti immediati in esercizio viene svolto con riferimento al modello di Koenig e Sherif, cioè applicando la teoria dell'elasticità (Boussinesque) ma riferendola ai soli strati di terreno compresi entro una profondità (sotto il piano di posa delle fondazioni) pari alla dimensione B del plinto (platea) o pari a 2 volte la dimensione B trasversale della trave di fondazione. Pertanto la somma degli spessori H da assegnare nella griglia di Input deve essere circa pari alla suddetta profondità.
Il programma prevede la discretizzazione della pianta della fondazione a partire dalla Mesh assegnata (se il numero di elementi discreti supera il valore di 1000 la mesh viene automaticamente incrementata). Calcolate per ogni rettangolo discreto le aree (tutte uguali), le coordinate dei baricentri e la risultante delle pressioni che su di esso insistono, viene costruita la matrice di deformabilità del terreno mediante i coefficienti riportati nel capitolo 4 del volume 'INTERAZIONE FONDAZIONE TERRENO' - Vincenzo Caputo - Ed. Hevelius.
Per tener conto dello spessore finito dei singoli strati di terreno considerati dette relazioni vengono modificate in base all'approssimazione di Streinbrenner (vedi vol. sopra citato).
In questo caso di fondazione infinitamente flessibile: nota la matrice di deformabilità ed i singoli carichi agenti sugli elementi è immediata la valutazione dei cedimenti dei baricentri singoli elementi discreti.
|
© GeoStru Software