Verificación de obras en represas artificiales
El criterio, descrito a continuación, de verificación de las barreras en represas artificiales es válido para obras con una altura de retención inferior a 15 metros.
Desde un punto de vista estático, un juicio global sobre las condiciones de estabilidad de la obra se puede deducir con un procedimiento aproximativo que subdivide la represa en dos partes: una aguas arriba y otra aguas abajo, cada una a examinar por separado.
La subdivisión se indica en el esquema de la Figura 1: la parte RMN está separada de la parte posterior MNS mediante un plano vertical que tiene como traza la recta MN.
De esta manera, el problema queda dividido en dos problemas parciales, que serán resueltos haciendo referencia a la unidad de espesor de la represa.
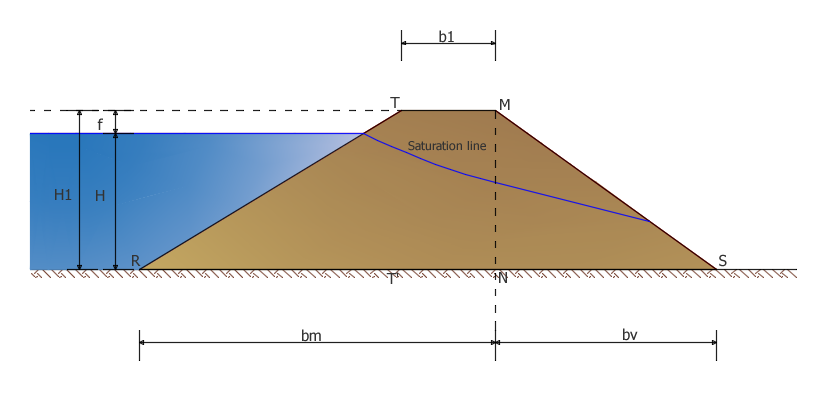
Figura 1
La parte aguas abajo MNS funciona como soporte de la parte aguas arriba presionada por el agua: la fuerza resistente que se opone al empuje transmitido por la parte aguas arriba se manifiesta, en cada cota, como un esfuerzo de corte agente a lo largo de la sección horizontal de base (sección más solicitada)
Las condiciones de verificación deberán satisfacerse con: embalse lleno, embalse vacío, embalse vaciado rápidamente.
EMBALSE LLENO
La condición de verificación se expresa mediante la desigualdad:
Tv ≤ Rv
Tv= S+Fo+Fv+Fs+FT representa el esfuerzo total de corte agente sobre la base NS y está constituido por las siguientes acciones:
S empuje hidrostático del agua embalsada
FO acción sísmica horizontal de la masa estructural
FV acción sísmica vertical de la masa estructural
FS acción inercial del agua embalsada
FT empuje del terreno aguas arriba de la sección MN
Rv por su parte representa la resistencia que el material es capaz de desarrollar. Se compone de una parte de rozamiento y de una cohesiva:
Rv=Pv (γs)·tanφ+c’·bv
Pv resultante de las acciones verticales función de γsisultante delle azioni verticali funzione di γs
c’ cohesión
EMBALSE VACÍO
El esfuerzo de corte total Tm agente en la sección de base está dado por la relación:
Tm=Fo+Fv+FT
La resistencia se expresa con:
Rm=Pm (γa)·tanφ+c’·bv
Pm representa el resultado de las acciones verticales, función de γa
EMBALSE RAPIDAMENTE VACIADO
En esta condición falta improvisadamente la acción de soporte que ejercita el empuje hidrostático contra el paramento aguas arriba, mientras que el cuerpo de la presa que no ha tenido el tiempo de vaciarse por filtración, queda empapado de agua. El esfuerzo de corte total Tm agente en la sección de base de la porción aguas arriba se define como:
Tm=[0.5·γS·H21·KA+0.5·γW·(2/3·H)2+kh·A(RTMSR)·γg]
La resistencia Rm se expresa con la fórmula:
Rm=Pm (γg)·tanφ
Pm representa el resultado de las acciones verticales, función de γgappresenta la risultante delle azioni verticali funzione di γg
El cálculo hidráulico de una represa en tierra tiene que ver con tres problemas: identificación de la llamada “línea de saturación”, cálculo de la capacidad de filtración, comprobación de sifonamiento.
La línea de saturación representa la más alta línea de flujo del movimiento filtrante, por debajo de todos los puntos de la línea de saturación el material está saturado con agua y en condiciones hidrostáticas, mientras que por encima falta la presión.
Es una curva convexa hacia arriba y puede determinarse gráficamente como se indica en la Figura 2.
Para estimar la capacidad de filtración por unidad de espesor de represa es necesario conocer el valor de la longitud promedio del recorrido de filtración, para lo cual se hace referencia a las relaciones empíricas disponibles en la literatura técnica.
A través de dicha longitud es posible cuantificar la capacidad mediante la siguiente relación:
Q=4/9·(k·H2/L)
donde:
k es el promedio de los dos coeficientes ko kv , coeficiente de permeabilidad ideal constante en todas las direcciones
L es la longitud promedio del recorrido de filtración
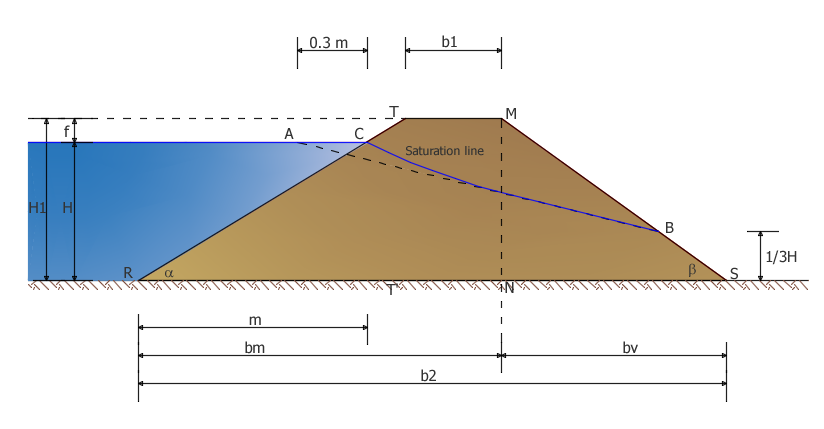
Figura 2
La verificación de sifonamiento se efectúa utilizando la relación empírica de Bligh en la forma:
La > cm·H
donde:
La desarrollo perimetral del perfil de cimentación
cm relación crítica de arrastre, depende de la naturaleza del terreno, puede asumir valores comprendidos entre un máximo de 20 para material incoherente finísimo y un mínimo de 4 para arcillas muy duras y compactas.
© GEOSTRU