Fino ad oggi il calcolo dei pali è stato effettuato sulla base di modelli di interazione palo-terreno di tipo essenzialmente elastico-lineare basati sul continuo elastico omogeneo e sull’interazione alla Winkler con coefficienti di sottofondo eventualmente variabili lungo il fusto del palo per considerare le variazioni stratigrafiche delle caratteristiche geotecniche.
La nuova normativa sismica (NTC 2008) richiede un calcolo non lineare dell’interazione palo-terreno ("nella caratterizzazione geotecnica è necessario valutare la dipendenza della rigidezza e dello smorzamento dal livello deformativo" § 7.11.2 NTC). Sarebbe inoltre necessaria una valutazione dell’interazione reciproca tra i pali in gruppo (§ 6.4.3 NTC) sottoposti, nel caso sismico, a forze orizzontali dinamiche e cinematiche.
Il calcolo dei pali in gruppo sottoposti ad azioni dinamiche di tipo sismico rappresenta uno dei capitoli più complessi ed ancora non del tutto esplorati dell'analisi strutturale. Non esistono soluzioni generali del problema che possano essere impiegate in un corrente programma di calcolo per uso professionale. Ricerche sono ancora in corso per validare metodologie di calcolo semplificate che evitino il ricorso a metodi generali di soluzione che dovrebbero analizzare la palificata mediante un'analisi dinamica non lineare al passo sotto un accelerogramma di progetto tenendo conto degli effetti dinamici di gruppo, della degradazione ciclica e dell'interazione sia con un terreno stratificato che con la struttura in elevazione. A causa della forte non linearità delle reazioni orizzontali del terreno lungo i pali, l'analisi modale in quanto lineare non è molto coerente. Come pure discutibile risulta l'uso delle impedenze (rigidezze funzione della frequenza espresse mediante numeri in campo complesso) in sostituzione delle rigidezze alla traslazione dei pali.
Una prima semplificazione del problema viene dal § 7.2.6 delle NTC quando a proposito della valutazione dell'interazione dinamica tra fondazione e terreno afferma che è "possibile" (non obbligatorio) "tenere conto della modifica del moto sismico indotta dall'interazione fondazione-terreno. ". Ciò a mezzo di vincoli visco elastici (impedenze dinamiche che tengano conto del livello deformativo....) specie per strutture alte e snelle con effetti del secondo ordine non trascurabili e per strutture fondate su terreno molto deformabili con Vs<100 m/s.
In questo programma sono previste le seguenti modellazioni alternative del terreno.
Pali nel modello di Winkler (lineare e non lineare)
Il calcolo degli spostamenti e delle sollecitazioni del palo viene effettuata dal programma considerando la sezione di estremità superiore del palo connessa alle travi o alla piastra di collegamento con vincolo di continuità o di cerniera sferica. Nel caso generale si possono calcolare pali in gruppo collegati tra loro a mezzo di una trave, di un graticcio di travi, di una piastra di forma qualsiasi (platea) semplice o nervata. L'interazione tra i pali e la struttura di collegamento orizzontale (testata) avviene unicamente in corrispondenza dei nodi principali in cui sono applicati i pali. In ogni nodo principale i gradi di libertà attivi sono costituiti, pertanto, dalle solite tre componenti di movimento considerate nel calcolo dei graticci e/o delle piastre (lo spostamento verticale e dalle due rotazioni intorno alla direzione degli assi X,Y del riferimento generale). A questi vanno aggiunte le tre componenti di movimento nel piano orizzontale, molto spesso uniche per tutti i nodi (spostamenti in direzione X,Y e rotazione intorno all'asse Z), con ciò trascurando le deformazioni assiali nel piano orizzontale X,Y in quanto sicuramente ininfluenti a causa delle massicce dimensioni usualmente impiegate per le strutture orizzontali di collegamento. In definitiva per poter assemblare nella matrice di rigidezza globale della struttura il singolo palo occorre costruire una matrice di rigidezza del palo che tenga conto dei sei gradi di libertà attivi in corrispondenza del nodo di innesto del palo nella testata. A tal fine ogni palo viene discretizzato in conci di trave aventi lunghezza vicina a quella assegnata come riferimento nella finestra dei dati generali. In ogni nodo di estremità dei conci viene applicata una molla non lineare che rappresenta la reazione trasversale del terreno lungo le due metà dei conci a cavallo del nodo. L'espressione analitica della reazione del terreno viene denominata in letteratura come curva p-y in cui p è la pressione del terreno e y è la corrispondente deformazione trasversale del palo. In generale ad ogni nodo della discretizzazione corrispondono parametri caratteristici differenti della curva p-y o addirittura curve di differente tipo nel caso di terreni di diversa natura attraversati dallo stesso palo.
Le curve p-y sono di tipo semiempirico e danno risultati molto aderenti al reale comportamento solo in presenza dello stesso tipo di terreno e di tecnologia di costruzione del palo in base ai quali sono state dedotte.
Se il terreno non corrisponde esattamente a quello di derivazione della curva p-y si consiglia di utilizzare le curve di tipo iperbolico (Carter 1984) definite dalla seguente legge costitutiva:
u = P/Ks [ Pu / (Pu - P ) ] n
in cui:
u = spostamento
P = pressione terreno in corrispondenza di u
Pu = pressione ultima terreno
Ks = coeff. di Winkler per piccole deformazioni (iniziali) del terreno
n = esponente che controlla l'estensione della non linearità. Il programma assume il valore di 1 per terreni coesivi e 0,25 per terreni incoerenti.
Questo tipo di legame costitutivo ha sempre fornito, nei controlli sperimentali effettuati, un'accettabile approssimazione in assenza di specifiche curve p-y per il particolare terreno incontrato.
Nella finestra dell'archivio pali sono esplicitate le espressioni analitiche delle varie curve p-y implementate dal programma, nonché una guida per la stima dei parametri geotecnici che le caratterizzano. Si sottolinea l'importanza della stima del valore ultimo Pu della pressione resistente del terreno ai fini di una realistica valutazione del carico limite trasversale del palo.
In maniera analoga vengono definite, in ogni nodo di discretizzazione del palo, molle non lineari che rappresentano le reazioni tangenziali assiali del terreno lungo il fusto del palo. Le funzioni di comportamento di tali molle vengono definite curve t-z con t che sta per 'tau' = tensioni tangenziali e con z che rappresenta la profondità in cui si valuta tale tensione. Nel programma viene proposta una curva t-z per terreni coerenti ed una per terreni incoerenti (da Reese - O'Neal) restando affidata all'utente (vedi stima Tu nella finestra dell'archivio pali) la determinazione del valore ultimo della tensione tangenziale del terreno; valore il cui peso è determinante per una corretta stima dei cedimenti assiali. Per la sezione di base del palo (anche di diametro differente da quella del fusto) il programma assume una curva di comportamento della reazione del terreno in funzione della pressione limite del terreno (raccomandazioni FHWA americane).
Ogni palo viene considerato dal programma come una sotto-struttura da assemblare nel sistema risolvente generale dell'intera struttura (metodo delle deformazioni) mediante i valori delle rigidezze del nodo di testa (matrice rigidezze 6x6 corrispondente ai 6 gradi di libertà della testa del palo). Risolto il sistema generale vengono aggiornate tutte le matrici di rigidezza dei singoli pali in funzione degli spostamenti ottenuti dalla risoluzione del sistema generale. Il sistema generale viene quindi riassemblato e risolto ottenendo nuovi spostamenti per i nodi di testa dei pali. Il procedimento viene iterato fino a che tutti gli spostamenti risultino pressoché uguali a quelli dell'iterazione precedente.
Pali immersi in terreno continuo elastico lineare
Anche in questo caso per poter assemblare il singolo palo nella matrice di rigidezza globale della struttura occorre costruire una matrice di rigidezza del palo che tenga conto dei sei gradi di libertà attivi in corrispondenza del nodo di innesto del palo nella struttura di collegamento. Il terreno è caratterizzato dal suo modulo elastico Es (costante o a variazione lineare con la profondità) ed il relativo coefficiente di Poisson µ. Il modulo elastico Es si può assumere costante nel caso di terreni argillosi sovraconsolidati, mentre per terreni incoerenti o argillosi normalconsolidati va assunto a variazione lineare a partire dal valore nullo in corrispondenza della testa del palo.
Per il calcolo dei coefficienti di rigidezza del singolo palo vengono fatte le seguenti posizioni:
Gs = 0.5 Es / (1+ µ) modulo di taglio del terreno
Ep modulo elastico secante del palo
R, L raggio e lunghezza del palo
G* modulo del terreno alla profondità L (alla punta)
r = 1 / 0,5 eterogeneità = 1 per Gs=cost./ eterogeneità = 0,5 per Gs variabile.
De = L [0,25 + (2,5 r (1- µ) – 0,25] distanza di estinzione
Ps = ln (De/R)
Ak = L tgh(mL) /(R mL)
mL = L / R ( 2 G* / (Ps·Ep))0.5
Lc = R / 2 ( Ep / G*)0.5 lunghezza caratteristica (tgh è la funzione tangente iperbolica)
Nel caso in cui risulti L < Lc si rientra nell’ipotesi di palo rigido assialmente e la rigidezza Kv , cioè la forza verticale che si sviluppa per uno spostamento verticale unitario, viene valutata con la seguente espressione:
Kv = 4 R G* (1-µ) + p L G*/4
Nel caso, invece, di palo deformabile (L > Lc) la stessa rigidezza viene così valutata (Randolph e Wroth 1978):
Kv = R·G*·Bk / Ck
in cui:
Bk = 4 / (1- µ) + 2 p r·Ak / Ps
Ck = 1 + 4 Ak·G*/ [p Ep (1-µ)]
Il problema del calcolo della rigidezza del palo per effetto di una forza orizzontale (o di una coppia) applicata sulla testa di un palo immerso in mezzo elastico avente modulo variabile linearmente con la profondità è stato brillantemente risolto da Randolph [8]. Le seguenti espressioni infatti consentono di correlare direttamente lo spostamento u e la rotazione t della testa di un palo prodotte dalla forza H orizzontale e dalla coppia M senza passare per la soluzione delle equazioni integrali:
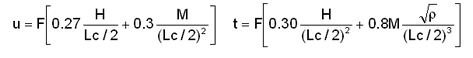
nelle quali:
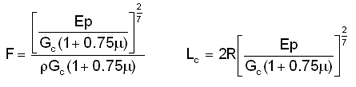
Lc = lunghezza critica per forza orizzontale
Gc = modulo di taglio alla profondità Lc/2
R = raggio sezione palo
r = G(z=L/4) / Gc = grado di eterogeneità
Il coefficiente r (grado di eterogeneità) vale 1 nel caso di modulo elastico del terreno costante, vale 0,5 nel caso di modulo del terreno linearmente variabile a partire dal valore nullo.
Nel caso di modulo Gs variabile il valore Gc da utilizzare per il calcolo di Lc è a priori incognito e va determinato per successive approssimazioni (insieme ad Lc) ricalcolando Lc più volte.
Affinché il comportamento del palo sia schematizzabile con le precedenti espressioni è necessario che la sua lunghezza L sia maggiore della sua lunghezza critica Lc (palo flessibile).
Le precedenti relazioni consentono di calcolare i coefficienti necessari a completare la matrice di rigidezza del palo, riportata in [6] nel caso di pali giacenti in un unico piano verticale.
Sforzi nei pali
Nel caso in cui si sia operato col modello alla Winkler (lineare o non lineare) la conoscenza degli spostamenti del nodo di testa dei singoli pali consente di determinare gli sforzi, le reazioni del terreno e gli spostamenti presenti lungo tutto il fusto dei singoli pali. Ai momenti così determinati il programma somma in automatico i momenti cinematici eventualmente assegnati in input. Il momento flettente di dimensionamento delle armature del palo viene assunto pari a quello avente il massimo modulo tra tutti quelli calcolati lungo il fusto del palo. Come sforzo normale associato a detto momento massimo viene sempre considerato quello calcolato in corrispondenza della testa del palo anche se non corrispondente alla sezione di momento massimo; ciò in quanto lo sforzo normale varia di poco nel tratto superiore del palo in cui si trova la sezione di momento massimo.
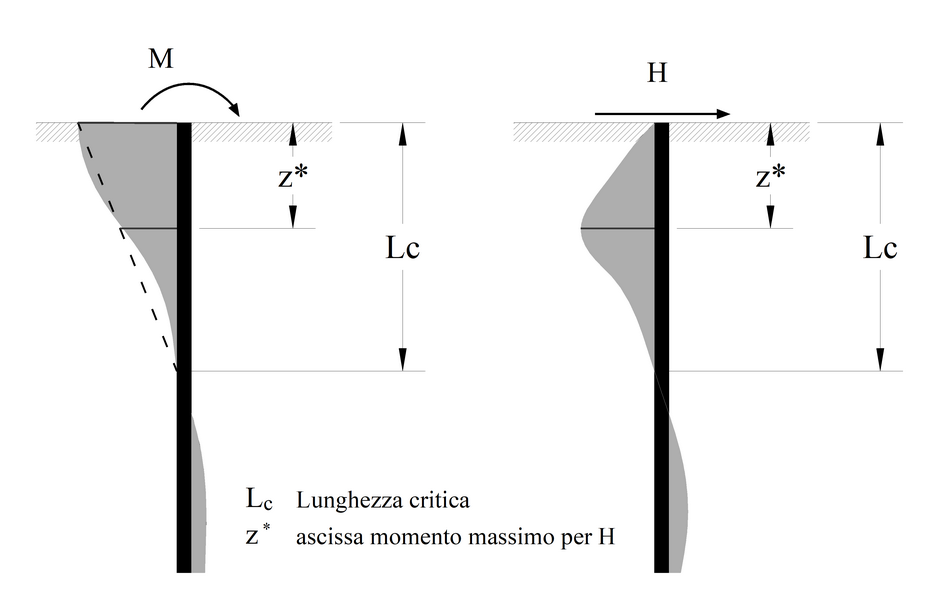
Nel caso invece del modello di terreno continuo elastico ed omogeneo il calcolo fornisce solo gli sforzi (H ed M di figura) e gli spostamenti del nodo di testa dei singoli pali. L'andamento dei diagrammi dei momenti flettenti prodotti separatamente da H ed M è del tipo rappresentato in figura. Il massimo momento flettente prodotto da H è fornito dalla espressione approssimata:
Mmax = 0,1 H Lc / r
tale valore massimo si ha in una sezione posta ad una distanza z* dalla testa pari a Lc/4 se Es è costante, pari a Lc/3 se Es è crescente linearmente con la profondità.
L'andamento del momento flettente lungo l'asse del palo andrebbe pertanto determinato per somma dei due diagrammi.
Poiché ai fini progettuali è importante stabilire solo il valore massimo del momento flettente il programma effettua il confronto tra i momento M che compete alla sezione di attacco del palo con quello M* relativo alla sezione in cui si sviluppa il momento massimo prodotto da H:
M* = 0,1 H Lc / r + c M
in cui c M è il valore del momento flettente dovuto ad M in corrispondenza della sezione in cui è massimo il momento prodotto da H; a tal fine l’andamento di questo ultimo diagramma dei momenti è schematizzato per semplicità come lineare a partire dal valore massimo pari a M fino al valore nullo alla profondità di Lc (vedi figura 4.1). In pratica il coefficiente di riduzione c vale 0,75 per r = 1 e 0,66 per r = 0,5. Si noti che la somma dei momenti flettenti da cui si ottiene M* è algebrica in quanto il segno dei momenti dipende dai versi di H ed M (tali momenti risultano quasi sempre di segno discorde).
Ai fini del calcolo delle armature e della relativa verifica il programma assume il momento flettente maggiore (in modulo) tra M ed M*.
Momenti cinematici
Questi momenti sono prodotti dalla deformazione del terreno in cui sono immersi i pali a seguito del passaggio delle onde sismiche. Le NTC al § 7.11.5.3.2 ne impone la valutazione per costruzioni di classe d'uso III o IV, per terreni di tipo D o peggiori in siti a sismicità media o alta (ag>0.25 g), e, nel caso in cui due strati adiacenti del terreno che circonda i pali presenti un forte contrasto delle rigidezze Gs (rapporto tra i due valori di Gs > 5).
Un calcolo rigoroso di questi momenti presenta notevoli difficoltà e risulta giustificato solo per opere di una certa importanza. Per opere correnti Gazetas (1997) propone una formula semplificata e conservativa con riferimento ad un terreno caratterizzato da due soli strati:
Mmax = 0,042 Ti d³ (L/d)0,3 (Ep/Es)0,65 (Va/Vb)-0,5
con
Ti = As Ro Ha = Tensione tangenziale all'interfaccia
Ro = densità strato superiore
As = accelerazione sismica di progetto alla superficie libera del terreno
Ha = spessore dello strato superiore
Va, Vb = velocità delle onde di taglio dello strato superiore ed inferiore
L, d = lunghezza e diametro del palo
Ep = modulo di Young del palo
Es = modulo elastico del terreno
Verifica sezioni circolari dei pali in c.a.
Viene effettuato il semiprogetto e la verifica della sezione circolare del palo maggiormente sollecitata a flessione come sopra determinata. Nel calcolo di verifica al momento massimo vengono sempre associati i valori dello sforzo normale del taglio e della torsione calcolati nella sezione di attacco del palo.
Nel caso in cui la struttura ricade in zona sismica il § 7.2.5 delle NTC richiede che i pali restino in campo elastico (come per tutti gli altri tipi di fondazioni) ed abbiano un'area di armatura longitudinale minima pari allo 0.3% di quella del calcestruzzo.
Nel caso di presenza dei momenti cinematici l'armatura massima del palo deve essere estesa a tutta la sua lunghezza.
Il programma progetta e verifica l'armatura necessaria ad assorbire gli sforzi derivanti dalle combinazioni di carico (amplificate col fattore di sovraresistenza gRd ) e dai momenti cinematici eventualmente assegnati.
Se il palo è calcolato mediante interazione lineare col terreno può accadere che uno o più pali non siano verificati nei confronti del carico limite per forza orizzontale pur essendo l'armatura ed il conglomerato verificati nei confronti delle massime sollecitazioni calcolate. Se ciò avviene per insufficienza del momento ultimo (ipotesi di palo 'medio' o 'lungo' nella teoria di Broms) si può intervenire nell'archivio sezioni travi/pali (§ 2.2.17) assegnando al numero minimo di barre di armatura della sezione del palo un valore superiore a quello fornito dal calcolo: reiterando il calcolo con armature via via crescenti si può giungere a soddisfare la verifica o si può decidere di modificare il diametro o la disposizione in pianta dei pali.
Calcolo pali in gruppo per carico verticale
Per pali in gruppo la vigente normativa non sismica (§ 6.4.3 NTC) prescrive la determinazione del carico ultimo complessivo della palificata tenendo conto degli effetti di gruppo. Detto Qult assunto per il carico ultimo del palo singolo il carico ultimo di una palificata comprendente N pali uguali può essere determinato in generale dalla seguente formulazione:
QGult = N E Qult
dove E è detto il fattore di efficienza della palificata.
Per terreni incoerenti E risulta non minore dell'unità e, cautelativamente, potrà sempre porsi 1. Per terreni coesivi si aggira intorno a 0,6, 0,7 e nel caso di m file di pali con n pali per ogni fila si potrà adottare la seguente formula empirica di Converse Labarre (cfr. [1]):
E = 1 – [2 arctg(i/d)/p ] [(m-1)n +(n-1)m]/ (n m)
dove i è l'interasse tra i pali di diametro d.
Nel caso di piccoli gruppi di pali (caso dei plinti su pali) conviene utilizzare valori predefiniti in base al numero di pali presenti in ogni plinto (metodo di Feld). Valori di riferimento del coefficiente E sono 1.00 per il palo singolo, 0.94 per palo doppio, da 0.82 per 4 pali a 0.72 per 9 pali. Per terreni a grana grossa va sempre assunto E=1.00.
E' sempre consigliabile scegliere un interasse tra i pali superiore a 3 volte il diametro dei pali, oltre che per motivi economici, anche per ridurre gli effetti dell'interazione che si verifica nel comportamento dei pali.
Calcolo interazione pali in gruppo per carico orizzontale
Questo tipo di calcolo è limitato al solo caso dell'interazione non lineare palo-terreno in quanto la matrice di rigidezza delle molle non lineari di ogni palo vengono modificate per ogni combinazione di carico a seconda della direzione delle forze orizzontali.
I pali in gruppo sollecitati da una forza orizzontale agente sulla testata di collegamento causano uno spostamento della testata stessa maggiore di quello che si avrebbe considerando la somma delle rigidezze dei pali prese isolatamente. L'interazione tra i pali dipende dal loro interasse (per interassi maggiori di 6 volte il diametro l'interazione diventa trascurabile), dalla direzione e dal verso del carico orizzontale applicato. Il metodo dei coefficienti di influenza descritto da Poulos in [4] con riferimento al continuo elastico ed ai soli carichi statici non conduce a risultati soddisfacenti nel caso di sollecitazioni dinamiche di natura sismica in quanto le rigidezze ridotte dei pali alla traslazione orizzontale pur risultando dipendenti dalla direzione della risultante sismica sono indipendenti dal relativo verso (in quanto non colgono l'effetto 'shadowing' rilevato sperimentalmente). Alle complicate soluzioni analitiche di tipo elastico che impiegano il suddetto metodo dei coefficienti di influenza in campo complesso (impedenze) si è preferito implementare nel programma il metodo dei P-moltiplicatori molto diffuso negli Stati Uniti in associazione all'uso delle curve P-y. I P-moltiplicatori sono fattori di riduzione empirica (il cui valore non superra 1,0) della curva caratteristica pressione-spostamento P-y. Essi sono ottenuti sperimentalmente da tests su pali in gruppo. L'abaco nella sottostante figura (proposto da R.L. Mokwa) viene utilizzato dal programma per la valutazione del valore dei moltiplicatori per ciascuna fila di pali ortogonale alla direzione della forza H applicata. Si noti che la fila di testa è la prima fila a destra quando la forza orizzontale è diretta da sinistra a destra. Detta fila di testa risulta più sollecitata delle file seguenti e, di conseguenza, ai pali che la compongono spetta il valore più alto del moltiplicatore. Le file successive a causa della sovrapposizione delle deformazioni a taglio del terreno (effetto 'shadowing') assorbono quote via via inferiori del carico orizzontale H. A patto di assicurare un interasse S maggiore di 3 volte il diametro del palo i moltiplicatori di una stessa fila possono essere assunti tutti uguali tra loro.
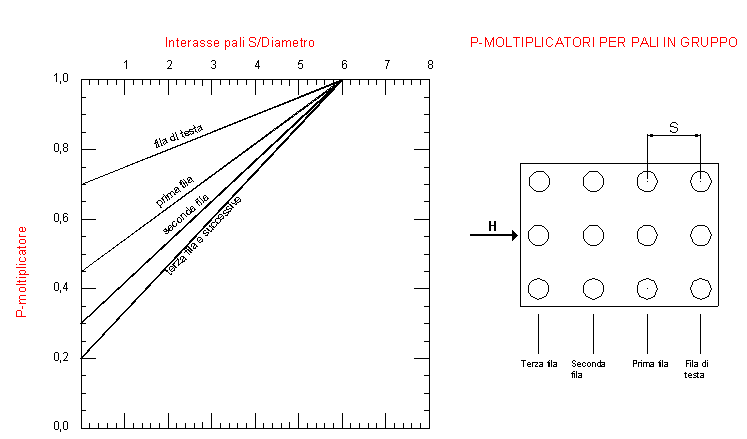
Il valore del moltiplicatore viene inoltre considerato costante lungo tutto il fusto di ognuno dei pali per cui tutte le curve costitutive p-y assegnate per un palo sono affette dallo stesso valore del moltiplicatore. Se nella finestra dei Dati Generali del programma si seleziona l'opzione relativa all'interazione orizzontale i detti moltiplicatori vengono applicati non solo ai pali con terreno cui si è attribuita una curva caratteristica p-y non lineare, ma anche ai pali calcolati con l'ipotesi di linearità elatica del terreno (pali all Poulos o alla Winkler con comportamento lineare elastico).
Calcolo micropali
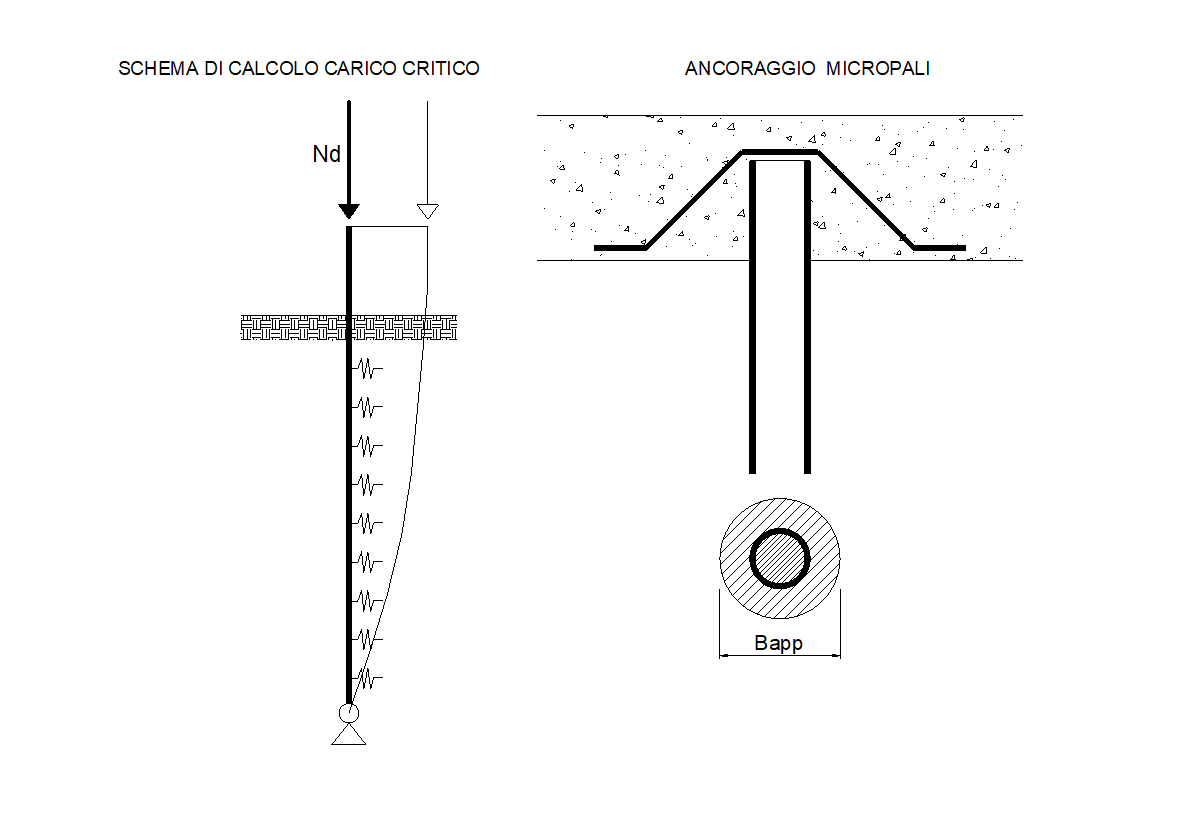
I micropali considerati nel programma sono quelli di più largo impiego risultando costituiti da un tubo da carpenteria in acciaio tipo Fe360 - Fe430 - Fe510. Tale tubo è circondato da un manicotto cilindrico di conglomerato cementizio, spesso iniettato dall'interno del tubo, la cui superficie esterna a contatto col terreno trasmette la portanza al micropalo sia in riferimento ai carichi assiali, sia in riferimento ai carichi trasversali per i quali si considera il diametro del manicotto (Bapp in figura) quale larghezza di contatto palo-terreno.
A favore di sicurezza si considera resistente alle sollecitazioni lungo tutto il palo la sola sezione tubolare in acciaio. A causa della notevole snellezza la verifica delle sezioni è sempre preceduta dalla determinazione del carico critico effettuato dal programma secondo lo schema rappresentato in figura. Nello schema il fusto del micropalo può avere un tratto superiore libero (modellazione eventuale distacco tra la testata ed il terreno), l'estremità superiore è considerata libera non solo di ruotare ma anche di traslare (a differenza degli schemi a cerniera fissa adottati da altri programmi); l'interazione palo-terreno lungo il tratto di palo immerso nel sottosuolo è modellata alla Winkler in base alle curve P-y (lineari o non lineari) assegnate nell'archivio tipologie pali; si trascura (a favore di sicurezza) la riduzione dello sforzo normale lungo il fusto trascurando le tensioni tangenziali assiali che si sviluppano lungo la superficie laterale a contatto col terreno; come conseguenza viene vincolata con cerniera fissa la sola estremità inferiore del micropalo. Il calcolo del carico critico viene effettuato con un procedimento iterativo che tiene conto sia della non linearità (eventuale) delle molle alla Winkler che di quella dovuti alle deformazioni del second'ordine che si sviluppano in funzione del carico applicato. Il palo tubolare in acciaio viene invece considerato a comportamento indefinitamente elastico. Per avviare il procedimento si assegna una deformazione iniziale dell'asse del palo rappresentata da una semiarco di sinusoide (vedi figura) con ampiezza massima (all'estremo superiore) pari ad 1/1000 della luce del palo. Il programma incrementa iterativamente il valore dello sforzo normale fino ad individuare il valore di N critico per il quale viene superato (biforcazione dell'equilibrio) lo spostamento ultimo prefissato per la testata dei pali.
Geostru Software ©