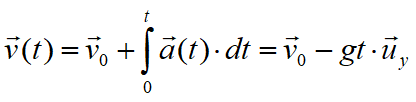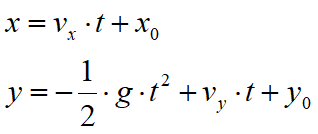Los presupuestos del modelo Lumped Mass son:
1. Esquema plano, perfil del talud semejante a un quebrado constituido por segmentos rectilíneos;
2. Bloque puntiforme y resistencia del aire insignificante.
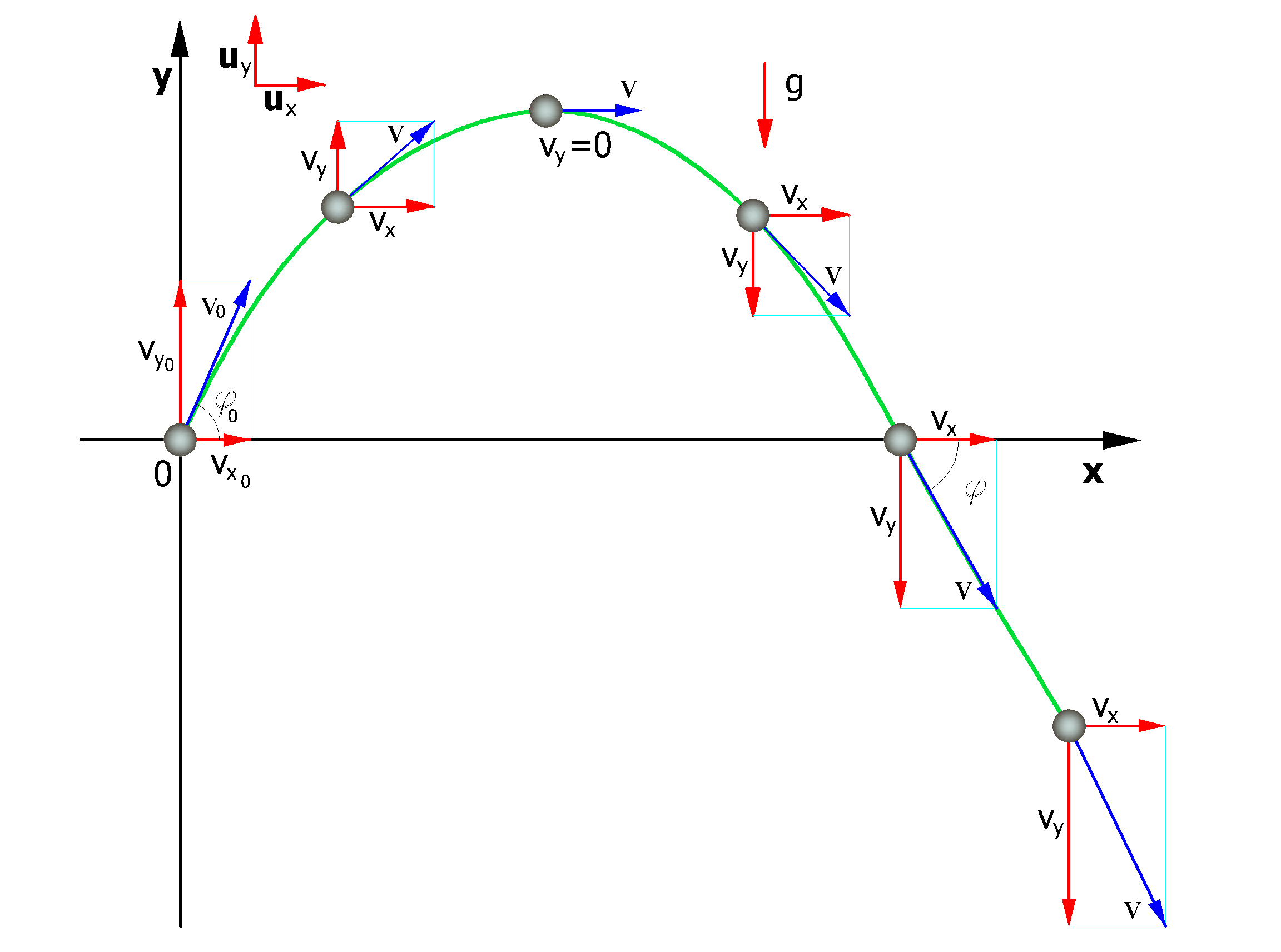
En tal caso la trayectoria del bloque se puede determinar utilizando las ecuaciones de movimiento de un grave.
El movimiento está caracterizado por una aceleración constante a=g=-guy y las condiciones iniciales son v=v0 al tiempo t=0, instante de lanzamiento. De la definición de aceleración en el movimiento plano se obtiene la siguiente relación:
puesto que
las velocidades de los movimientos proyectados en los ejes son:
|
|
Haciendo referencia a un sistema de ejes cartesianos ortogonales, tales ecuaciones son:
|
(1) |
donde:
vx componente horizontal de la velocidad del bloque;
vy componente vertical de la velocidad del bloque;
t tiempo;
g aceleración de gravedad;
x0 abscisa del punto donde el bloque se desprende del talud o donde golpea durante la caída;
y0 ordenada del punto donde el bloque se desprende del talud o donde golpea durante la caída.
A lo largo del eje x el movimiento es uniforme, mientras que en el eje y el movimiento es uniformemente acelerado.
A lo largo del eje x el movimiento es uniforme, mientras que en el eje y el movimiento es uniformemente acelerado.
De este modo la trayectoria del movimiento resulta compuesta por una serie de parábolas trazadas entre el punto donde se dio el desprendimiento y el punto donde el bloque choca contra el talud por primera vez, en la fase inicial del movimiento; y entre dos puntos sucesivos de impacto en el talud, o al pie, seguidamente, hasta el punto final de parada.
Las coordenadas de los puntos de impacto y los componentes de la velocidad se determinan resolviendo el sistema entre las ecuaciones (1) y las ecuaciones de las rectas que representan el perfil del talud.
En la práctica, se procede desde el punto en donde se despega del bloque y se resuelve tal sistema de ecuaciones considerando en cada caso las diferentes ecuaciones de las rectas que contienen los sucesivos segmentos hasta encontrar las coordenadas de un punto, punto de impacto que pertenece a la parábola que representa la trayectoria y cae al interno de uno de los segmentos y que es, por lo tanto, también un punto del talud.
Tal punto representa el primer punto de impacto del bloque en el talud. El procedimiento se repite partiendo desde ese punto para determinar el sucesivo arco de la trayectoria y un nuevo punto de impacto.
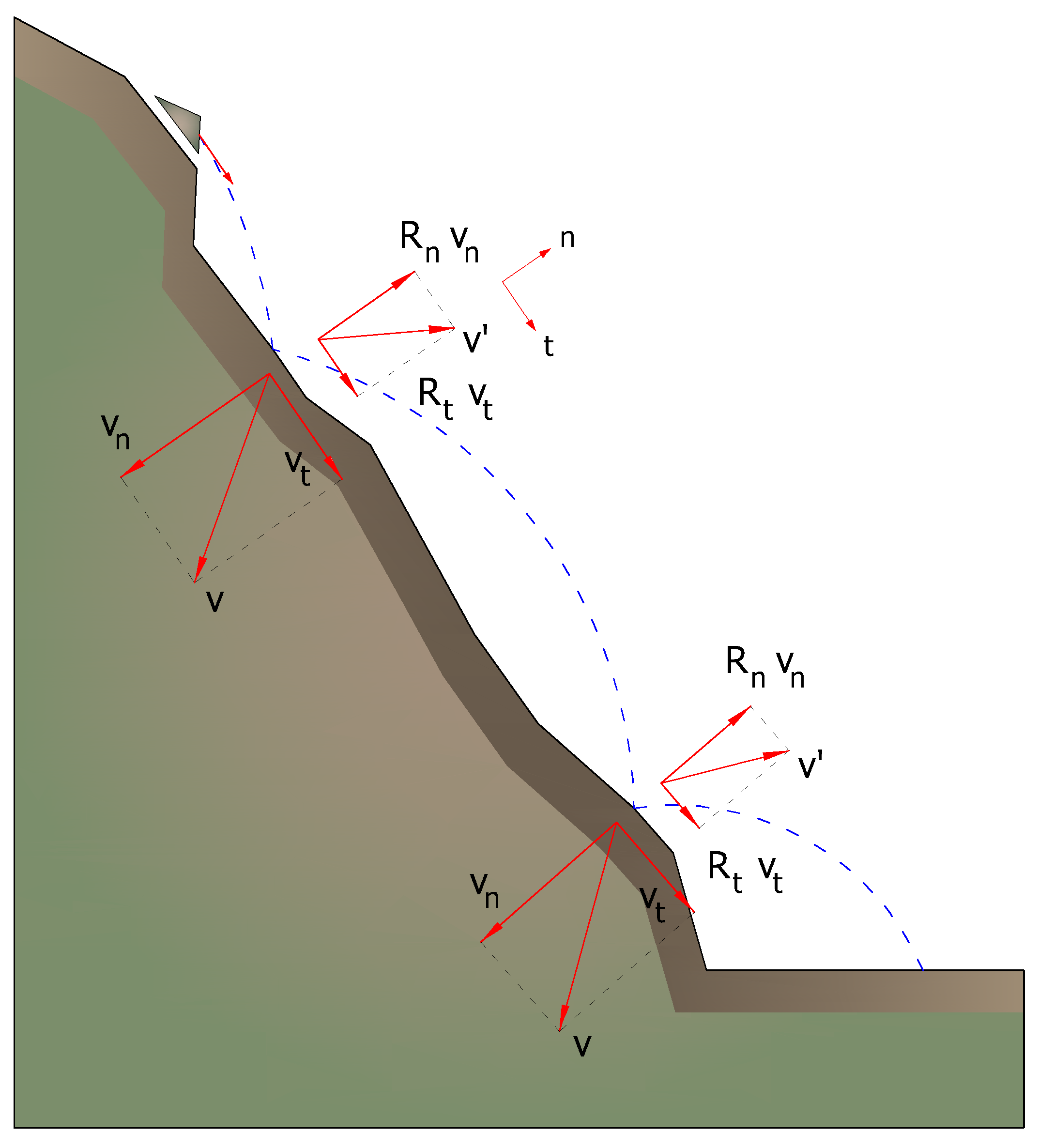
La pérdida de energía cinética por el efecto de los rozamientos y de los choques se puede modelar reduciendo la velocidad del bloque en caída cuando este choca contra el talud.
En particular, indicando con vn y vt componentes (normales y tangenciales) de la velocidad antes del choque, después del choque v'n, v't se pueden calcular mediante las relaciones:
![]()
Rn y Rt son coeficientes de restitución variables en el intervalo 0-1.
|
© GEOSTRU- GeoRock 2D