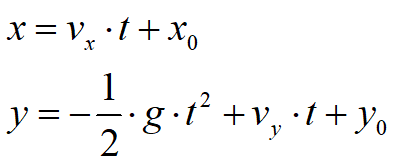Le ipotesi del modello Lumped Mass sono:
1. schema piano, profilo del pendio assimilabile ad una spezzata costituita da segmenti rettilinei;
2. blocco puntiforme e resistenza dell' aria trascurabile.
In tal caso la traiettoria del blocco può essere determinata utilizzando le equazioni del moto di un grave
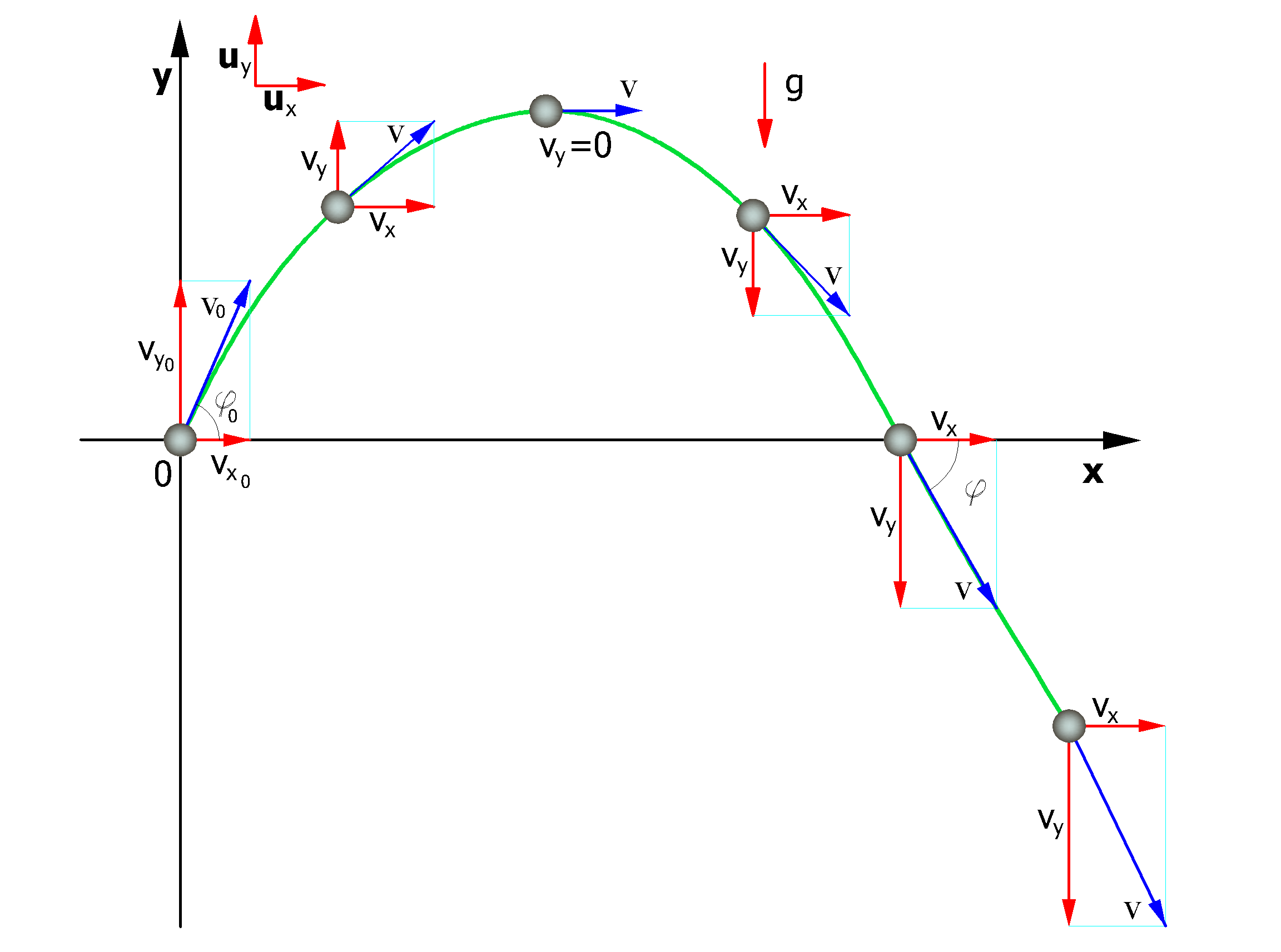
Il moto è caratterizzato da un'accelerazione costante a=g=-guy e le condizioni iniziali sono v=v0 al tempo t=0, istante di lancio.
Dalla definizione di accelerazione nel moto piano si ricava la seguente relazione:
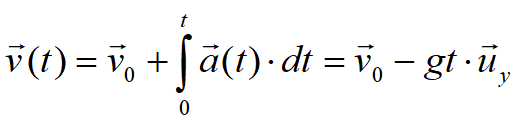
poichè
![]()
le velocità dei moti proiettati sugli assi sono:
![]()
![]()
Facendo riferimento allo stesso sistema di assi cartesiani ortogonali le leggi orarie dei moti proiettati sono:
|
(1) |
dove:
vx componente orizzontale della velocità del blocco;
vy componente verticale della velocità del blocco;
t tempo;
g accelerazione di gravità;
x0 ascissa del punto in cui blocco si distacca dal pendio o urta nel moto di caduta;
y0 ordinata del punto in cui blocco si distacca dal pendio o urta nel moto di caduta.
Lungo l'asse x il moto è uniforme, lungo l'asse y uniformemente accelerato.
In tal modo la traiettoria del moto del blocco risulta composta da una serie di parabole tracciate fra il punto in cui avviene il distacco ed il punto in cui il blocco urta sul pendio per la prima volta, nella fase iniziale del moto, e fra due successivi punti di impatto sul pendio, o al piede, in seguito, fino al punto finale di arresto.
Le coordinate dei punti d' impatto e le componenti della velocità si determinano risolvendo il sistema fra le equazione (1) e l' equazione delle rette che rappresentano il profilo del pendio.
In pratica si procede dal punto in cui avviene il distacco del blocco e si risolve tale sistema di equazioni considerando di volta in volta le diverse equazioni delle rette che contengono i successivi segmenti della spezzata fino a trovare le coordinate di un punto, punto di impatto, che appartiene alla parabola che rappresenta la traiettoria e ricade all' interno di uno dei segmenti della spezzata ed è pertanto anche un punto del pendio.
Tale punto rappresenta il primo punto di impatto del blocco sul pendio. Il procedimento viene ripetuto a partire da tale punto per determinare il successivo arco della traiettoria ed un nuovo punto d' impatto.
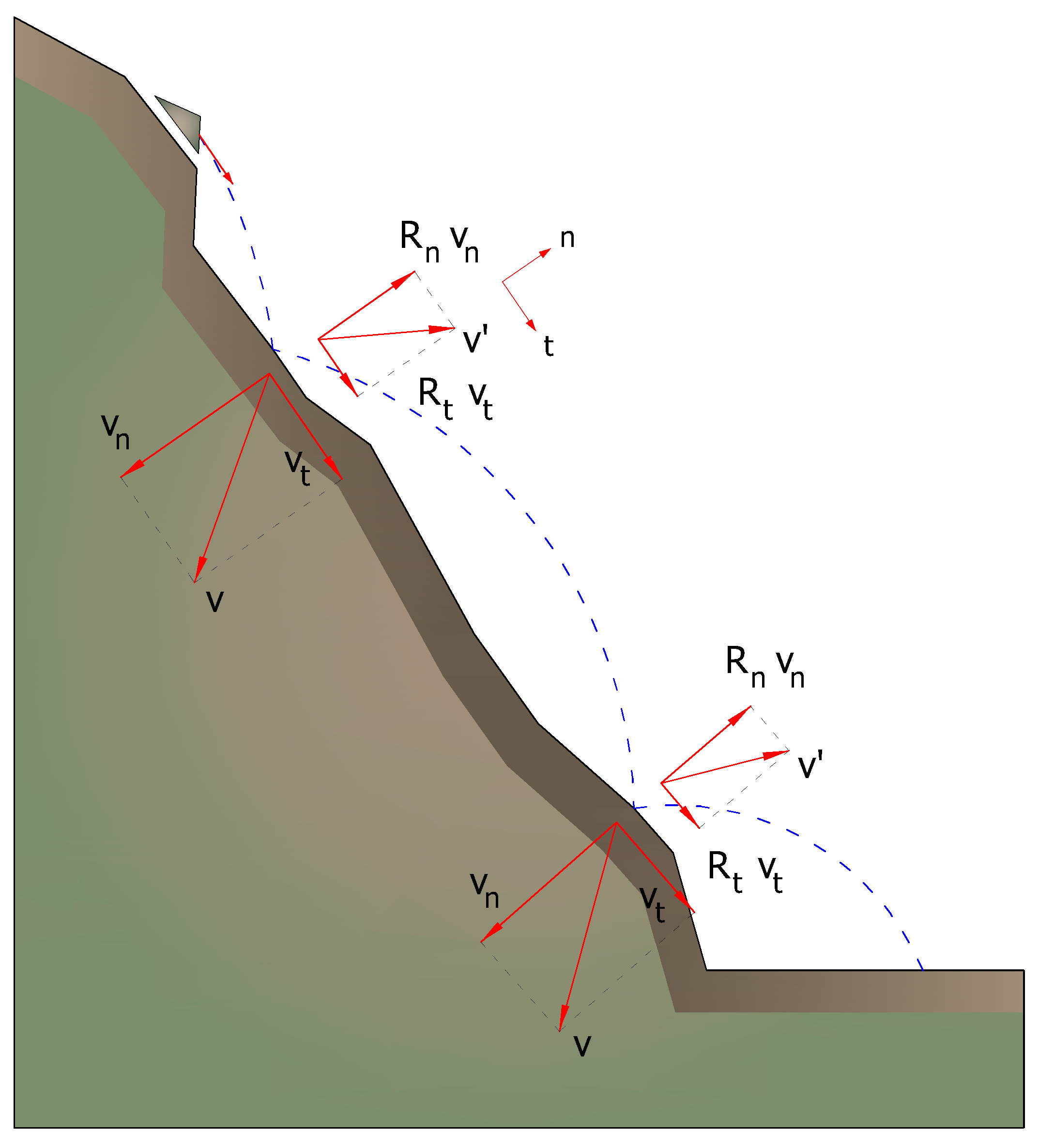
La perdita di energia cinetica per effetto degli attriti e degli urti può essere modellata riducendo la velocità del blocco in caduta ogni qualvolta questo urta sul pendio.
In particolare, indicando con vn e vt le componenti (normali e tangenziali) della velocità prima dell' urto, dopo l'urto v'n, v't possono calcolarsi mediante le relazioni:
![]()
Rn ed Rt sono detti coefficienti di restituzione variabili nell' intervallo 0-1.
|
© GEOSTRU- GeoRock 2D