Tensiuni in situ și condiții de repaos (K0)
In situ, forța verticală care acționează asupra planului generic la adâncimea z poate fi calculată în general, ca suma contribuțiilor a n straturi de greutate specifică γi și grosime zi.
Forța verticală efectivă prezentă în sol este mai mare decât presiunea laterală în același punct. Raportul dintre forțele laterale și verticale este definit ca:
K=σh/P0
valabil la orice adâncime și în fiecare moment.
Când forțele se stabilizează în jurul unei valori constante, fără deformare, forțele devin principale, acționând asupra planurilor principale; această stare de tensiune este numită în repaus sau în starea K0, unde K0 este definit ca:
K0=σ'h/P'0
Jaky (1948)
Corelație valabilă pentru toate materialele granulare
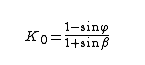
φ: Unghiul de rezistență la forfecare;
β: Înclinația profilului;
Alpan(1967)
Corelație valabilă pentru argilele normal consolidate:
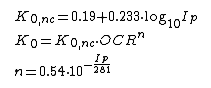
Ip: Indicele de plasticitate în % logaritm în baza 10;
OCR: Raportul de supraconsolidare;
Presiunea laterală a terenului
Presiunea laterală a solului este un parametru semnificativ de proiectare în diferite probleme de inginerie. Pentru ziduri de sprijin, pereți mulați, excavări, pentru calcularea presiunilor exercitate asupra peretelui unui siloz, pentru evaluarea presiunii pământului sau a rocii asupra pereților tunelurilor sau a altor structuri subterane. Pentru estimarea presiunii laterale, se utilizează în general metoda echilibrului plastic definită de Mohr.
Coulomb 1776
Una dintre primele metode de estimare a presiunilor exercitate asupra zidurilor de sprijin este atribuită lui Coulomb, care a făcut o serie de ipoteze:
•Sol izotrop;
•Suprafață plană de rupere;
•Rezistența la frecare distribuită uniform de-a lungul suprafeței de rupere;
•Pană de rupere se comportă ca un corp rigid;
•Există frecare între zid și teren;
•Ruperea are loc în condiții de deformare plană.
Principalele limitări ale teoriei lui Coulomb sunt de a lua în considerare un teren ideal și de a emite ipoteza comportamentului ideal.
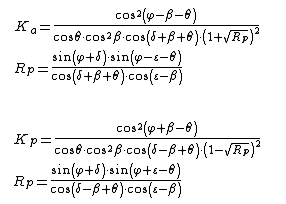
φ: unghiul de rezistență la forfecare;
ε: înclinare versant în amonte;
θ: unghiul seismic;
δ: Unghiul de frecare zid-sol;
β: înclinarea parametrului intern în raport cu verticala
NB: În formula lui Coulomb θ = 0.
Rankine 1857
Coeficienții împingerii active și pasive, în ipoteza unui sol omogen și uscat cu planul orizontal de referință, iau următoarele valori:
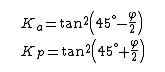
φ:unghiul de rezistență la forfecare;
Muller Breslau 1924
Nu se impune condiția ca solicitările orizontale și verticale să fie principale.
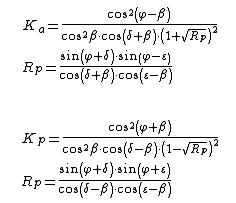
φ: unghiul de rezistență la forfecare;
ε: înclinare versant în amonte;
δ: Unghiul de frecare zid-sol;
β: înclinarea parametrului intern în raport cu verticala
Mononobe e Okabe 1926
Modelul Mononobe și Okabe este similar cu formularea lui Muller Breslau, se diferențiază prin introducerea efectului cutremurului.
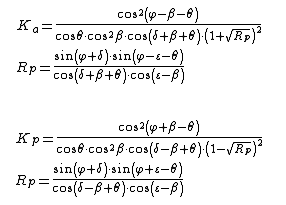
φ: unghiul de rezistență la forfecare;
ε: înclinare versant în amonte;
θ: unghiul seismic;
δ: Unghiul de frecare zid-sol;
β: înclinarea parametrului intern în raport cu verticala
NB: În formula lui Coulomb θ = 0.
|
© Geostru