Barriere paramassi rigide ed elastiche

Le barriere paramassi a rete sono generalmente composte da una struttura d’intercettazione, da una struttura di sostegno, da una struttura di collegamento e da una struttura di fondazione.

Questo tipo di barriere vengono suddivise in due categorie:

1.barriere a limitata deformabilità (rigide), progettate per arrestare il masso in spazi ridotti;

2.barriere ad elevata deformabilità (flessibili), progettate per arrestare massi con elevate energie attraverso un lavoro sia elastico che plastico.

Le barriere a rete offrono un limitato impatto ambientale, una limitata invasione dell’ambiente in fase di messa in opera, rapidità di esecuzione dell’intervento, possibilità di collocazione della barriera a qualsiasi altezza, un notevole abbattimento del rischio se collocate su più file, adattamento al profilo del terreno, costi contenuti e facile manutenzione e ripristino.

L’opera di difesa deve essere in grado di resistere all’impatto e di dissipare l’energia cinetica posseduta dal masso.

1) barriere a limitata deformabilità

Nella maggior parte dei casi il masso colpisce la rete, che, deformandosi, dissipa l’energia cinetica dell’impatto.

L’energia dissipata si può calcolare attraverso la seguente relazione:

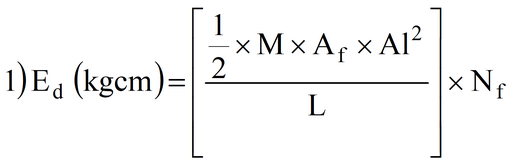
dove

M = modulo elastico delle funi, in genere posto uguale a 220.000 kg/cmq;

Af (cm2) = p x (Df / 2)2, area trasversale delle funi;

Df (cm) = diametro delle funi;

Al (cm) = (ap / 100) x L, allungamento massimo delle funi;

ap (%) = allungamento percentuale della fune, in genere pari a 8;

L (cm) = lunghezza totale della singola fune;

Nf = numero di funi coinvolte nell’impatto

2) barriere ad elevata deformabilità

Quando l’energia dissipabile dalla rete è minore di quella prevista per l’impatto più violento (Ed < Ecmax), si utilizzano le barriere elastiche nelle quali entrano in funzione i dissipatori di energia. Un dissipatore consiste in un cappio di fune d’acciaio chiuso da un blocchetto di frizione. Quando il masso impatta contro la rete, il cappio tende a scorrere all’interno del blocchetto di frizione, dissipando per attrito una frazione dell’energia cinetica del masso impattante.

L’energia dispersa dai dissipatori è data da:

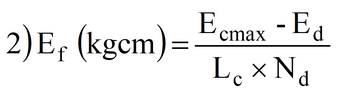
dove

Ecmax – Ed = frazione di energia cinetica non dissipata dalla deformazione della rete;

Lc = lunghezza del cappio, generalmente 90 cm;

Nd = numero di dissipatori che entrano in funzione.

La pressione esercitata dai blocchetti nel serraggio, invece è data:

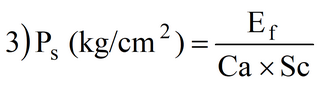
dove

Ca (cm) = coefficiente d’attrito acciaio-acciaio, uguale a 0,2;

Sc (cm2) = superficie di contatto fune-blocchetto, pari a [2 / 3 (p Df) – (0,2 x 0,2)] x l

l (cm) = lunghezza del contatto fune-blocchetto.

3) L’urto viene assorbito dai puntoni

Se il masso impatta con uno dei puntoni d’acciaio che sostengono le reti, bisogna verificare la quantità di energia che può essere dissipata nell’urto e la necessità di eventuali ancoraggi.

L’energia cinetica dissipata è data da.

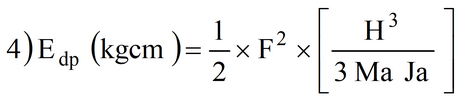
con

F (kg) = Mra x Sa / H, massima forza assorbita dal puntone in fase elastica;

Mra (cm3) = modulo di resistenza dell’acciaio;

Sa (kg/cm2) = resistenza a trazione dell’acciaio;

H (cm) = altezza fuori terra del puntone;

Ma (kg/cm2) = modulo elastico dell’acciaio;

Ja (cm4) = momento d’inerzia dell’acciaio.

La corrispondente massima deformazione dell’acciaio è data da:

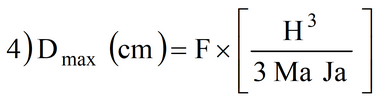
Nell’ipotesi che la deformazione dei puntoni rimanga in fase elastica, l’energia cinetica assorbita dagli ancoraggi sarà data da:

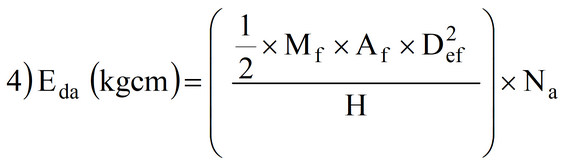
dove

Mf (kg/cm2) = modulo elastico della fune;

Def (cm) = Dmax/cos2q, allungamento della fune relativa alla massima deformazione elastica del puntone;

q (°) = angolo fra ancoraggio e puntone;

Na = numero degli ancoraggi sollecitati.

Se però viene presa in considerazione la massima deformazione che può essere assorbita dalle funi si ottiene:

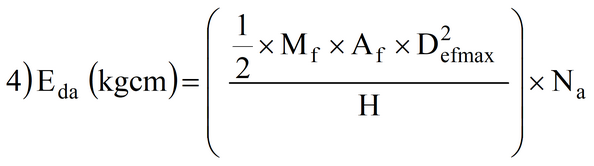
dove

Defmax (cm) = (Almax/100)xLt, allungamento massimo sopportabile dalla fune d’acciaio;

Almax (%) = allungamento percentuale massimo della fune;

Lt (cm) = lunghezza totale della fune.

Terrapieni e muri paramassi

I rilevati paramassi in terra rinforzata, a struttura trapezoidale, costituiti da materiale grossolano eventualmente armato con geogriglie, servono a proteggere infrastrutture di notevole estensione, tanto che lo sviluppo longitudinale dell’opera può superare il centinaio di metri con altezze di 6 ¸ 8 m e larghezza di 10 ¸ 12 m alla base e 4 ¸ 5 m alla sommità.

A completamento dell’opera, immediatamente a monte del rilevato, un vallo, scavo sagomato, che serve a rallentare i massi in caduta e di raccoglierli.

I muri rigidi, usati per creare un ostacolo a massi fino a 2 m3, sono dimensionati come un muro a gravità soggetto all’azione dinamica del masso e presentano generalmente anch’essi a monte un vallo.

Infine esistono strutture miste in cui il terrapieno è sostenuto a monte da un muro o da una gabbionata.

Nel caso di terrapieno la profondità di penetrazione può essere valutata con la seguente relazione di Kar (1979). Si calcola prima la variabile Z con la:

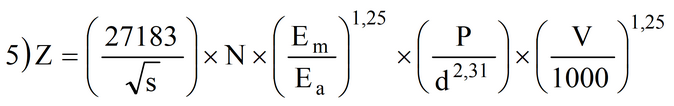
dove

s (kPa) = resistenza alla compressione semplice della struttura;

N = fattore di forma pari a 1 per masso appuntito o a 0,72 per masso a forma piatta;

Em (kPa) = modulo di elasticità del masso;

Ea (kPa) = modulo di elasticità della struttura (usare il modulo di elasticità dell’acciaio);

P (kg) = peso del masso;

d (m) = diametro massimo del masso;

V (m/s) = velocità d’impatto del masso.

Quindi si calcola la profondità di penetrazione dalle:

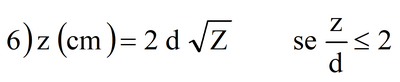
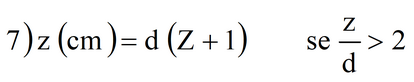
Poiché sono possibili entrambe le due soluzioni, si procede prendendo in considerazione il valore maggiore e verificando che sia soddisfatta la condizione z/d, altrimenti si assumerà come risultato l’altro valore di z calcolato.

Nel caso di una struttura muraria o in calcestruzzo, invece, si ha:

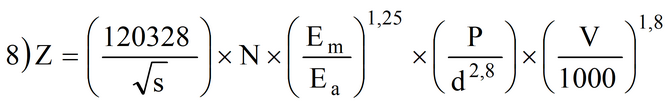
La forza d’impatto di un masso su una struttura può essere valutata partendo dalle esperienze di McCarty & Carden (1962), Karr (1979), Knight (1980):

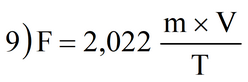
dove

m (kgf) = massa del blocco roccioso pari a P/g;

g (m/s2) = accelerazione di gravità;

T (s) = durata dell’impatto.

Il valore di T è dato dalla:

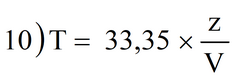
dove z è data in m e V in m/s.

La sollecitazione massima sulla struttura, sia essa un terrapieno o un muro, sarà:

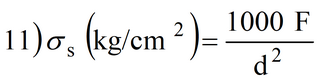
A volte, a monte, i terrapieni sono sostenuti da un muro in calcestruzzo o da una struttura muraria, per cui nel calcolo si utilizza dapprima la 5). Qualora risultasse che il masso penetra per una profondità superiore allo spessore del muro, bisognerà valutare la velocità residua:

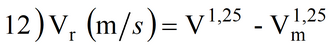
dove Vm (m/s) è la velocità minima necessaria per attraversare il muro.

Vm si calcola ponendo il valore dello spessore del muro al posto del parametro z nella 6) o nella 7), a seconda del rapporto (spessore muro/d), quindi si determina Z e si calcola Vm dalla 8).

La penetrazione del masso, con velocità residua Vr, nel terrapieno, si valuterà con la 5).