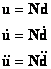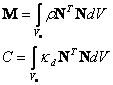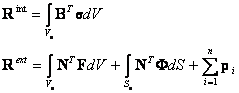<< Click to Display Table of Contents >> Navigation:  »No topics above this level« Dynamic and seismic analysis

 

Equations that govern the dynamic response of massive will be derived by requiring the work of external forces to be absorbed by the work of internal, inertial and viscous forces for any small kinematically admissible motion. For a single element we can write:

 

 

where:

- small arbitrary dislacements

small arbitrary strains vector

F- body forces vector

Φ - prescribed surface tractions

pi concentrated loads vector

- the displacement of the point at which load pi is applied.

ρ - mass density of the material

κd material damping parameter

Denoting with N the shape functions of the finite elements, we have for the displacement field u and its two first time derivatives (velocities and acceleration fields):

 

                                                           

Where the vector d contains the displacements at nodes of the finite element that are functions of time only.

Combining the equations (212) and (213) and since the displacements are arbitrary we obtain the following coupled, second-order, ordinary differential equations in time:

 

                                               

where the element mass and damping matrices are defined as:

 

                                                                                                   

and the element internal force and external load vectors are defined as:

 

                       

An undamped structure, with no external loads applied to unrestrained d.o.f., undergoes harmonic motion in which each d.o.f. moves in phase with all other d.o.f. This way:

 

                                         

Combining Eq.(214) and Eq.(217) and setting C=0 and Rext=0 we obtain:

 

                                 

Which represents the basic statement of the vibration problems and where K represents the stiffness matrix of the structure and M the global mass matrix that may be „lumped” or „consistent”.

The consistent element mass matrix is defined by the following relation:

 

                               

Where N represents the shape functions matrix. The lumped mass matrix is obtained by placing particle masses mi at nodesi of an element such that is the total element mass. A lumped mass matrix is diagonal but a consistent mass matrix is not. For a 4 noded quadrilateral, for example, the lumped mass matrix is given by:

 

                                         

where A is the element area and I the unit matrix.

 

 

 

 

 

 

 

 

© GeoStru Software