The finite element method requires dividing the analysis region into several sub-regions. These small regions are the elements, which are connected with adjacent elements at their nodes. Mesh generation is a procedure of generating the geometric data of the elements and their nodes, and involves computing the coordinates of nodes, defining their connectivity and thus constructing the elements. Here, mesh designates aggregates of elements, nodes and lines representing their connectivity. Capability and convenience of modeling the analysis domain are dominated by the mesh generation procedure. The geometric characteristics of generated elements affect the overall performance and accuracy of the finite element analysis. Therefore, mesh generation is one of the most important procedures in finite element modeling.
A mesh of isoparametric quadrilateral or triangular is automatically generated and optimized during analysis. You can specify the grid spacing in the X and Y-directions as part of the analysis parameters. A finer grid will often improve accuracy. However, the time taken to perform an analysis is a function of the number of finite elements – the finer the grid, the longer the analysis time.
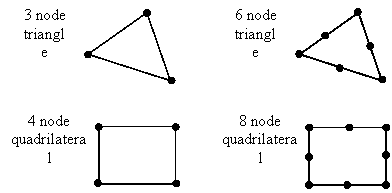
GFAS uses two types for finite element mesh generation: block mesh generator (structured mesh) that requires some initial form of gross partitioning and unstructured mesh generator (constraint automatic triangulation). In the first approach the solution domain is partitioned in some relatively small number of blocks. Each block should have eight-node quadrilateral form. Mapping technique generates the mesh inside the block. In the second approach the mesh is generated for an arbitrarily shaped region. The mesh is generated simply by designating the curves of the mesh boundary and issuing a mesh generation command. A curved surface as well as a plane may be meshed by this method. Also you can generate a coarse mesh (i.e. the gross geometry of the model) that can be refined later using the tools provided by GFAS specifically for this purpose. Removal of elements and renumbering of the mesh options are also allowed through the GFAS processors. During the mesh generation phase it is not required to make a decision on the element type to be used. Only the element class is important at this stage (triangular or quadrilateral). For instance: 3-noded triangular elements can be used to generate the mesh and then the entire mesh can be converted to the higher-order 6-noded triangle elements. In the phase of the analysis definition it has to be decided if the element is axisymmetric, plane stress or plane strain.
The basic mesh generator features include:
ÜAutomatic mesh generation: T3, T6, Q4, Q8.
ÜNodes renumbering: Reverse Cuthill-McKee algorithm implemented for T3, T6, Q4, Q8 finite elements meshing.
ÜTransform simple (T3, Q4) to higher order finite elements(T6, Q8).
ÜRegions and Material data recognition: after mesh generation, properties such as material type(for each finite element) and region subdivision can be revealed in the framework of the further mesh manipulation.
ÜMesh refinements: automatic mesh refinement for all of the above finite elements types (T3, Q4, T6, Q8).
ÜMask finite elements: Allowed to cut selected elements in order to create complex geometry.
|
Fig.1. Element types in mesh generation. |
© GeoStru Software