Si vuole analizzare un problema di stabilità di versante: i materiali sono caratterizzati dal modello costitutivo di Mohr-Coulomb e i carichi agenti sono essenzialmente di tipo gravitazionale. La verifica consiste nel calcolare il fattore di sicurezza (FS), definito come il rapporto fra tan F' (angolo d’attrito interno) e c (coesione), che viene gradualmente ridotto fino a rottura, mantenendo costanti i carichi gravitazionali. In Figura 48 sono riportati i dati geometrici del pendio omogeneo oggetto di analisi, mentre le proprietà dei materiali e le caratteristiche di resistenza si riassumono in Tabella 5. In questo caso specifico non si considera la variazione di volume che avviene durante la rottura e si pone pari a 0 il valore dell’angolo di dilatanza.
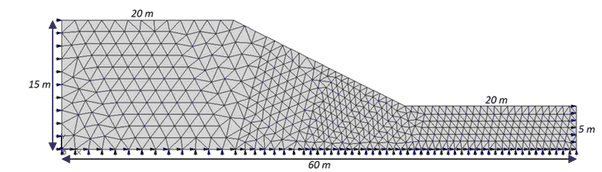
Fig. 48. Mesh e dati dell’analisi di stabilità del pendio.

Tabella 5. Proprietà dei materiali
Il modello tiene conto del carico gravitazionale e il fattore di riduzione della resistenza (SRF) aumenta in maniera graduale finché non si verifica la convergenza.
I risultati dell’analisi sono riportati in Tabella 6, in cui sono stati indicati i fattori di resistenza ridotti con i corrispondenti valori dei massimi spostamenti nodali associati ed il numero di iterazioni necessarie ad ottenere la convergenza.
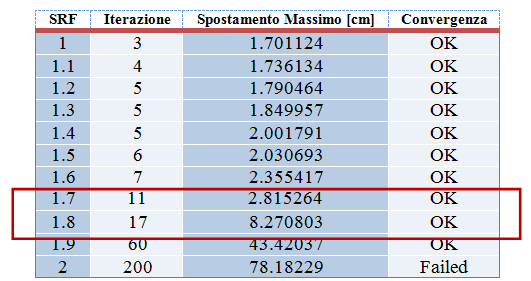
Tabella 6. Sintesi dei risultati raggiunti dall’analisi di stabilità del pendio
La convergenza fallisce quando il valore di SRF è pari a 2, ma, osservando in modo critico i risultati raggiunti, si può dire che già da un SRF pari a 1.6 i valori ottenuti non risultano accettabili: si registra infatti, una prima variazione di 0.5 cm (passando da FS=1.6 a FS=1.7), e successivamente una variazione di ben 5 cm, al passaggio da FS=1.7 a FS=1.8.
I risultati dell’analisi sono rappresentati nel grafico riportato in Figura 48: si può osservare come gli spostamenti aumentino rapidamente dal valore di SRF pari a 1.7 in poi.
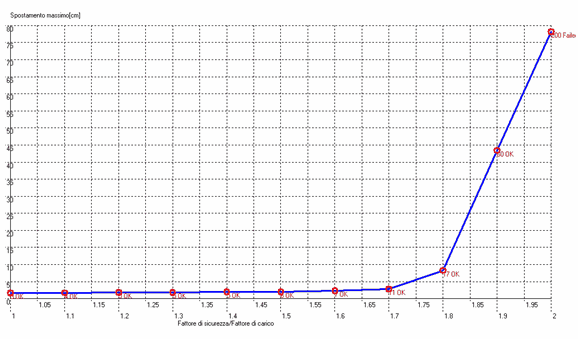
Fig. 48. Grafico del massimo spostamento e del Fattore di Riduzione della Resistenza (SRF).
Nelle Figure 49 e 50 sono rappresentate la mesh deformata a rottura e gli spostamenti registrati: il meccanismo di rottura è chiaramente localizzato al piede del pendio.
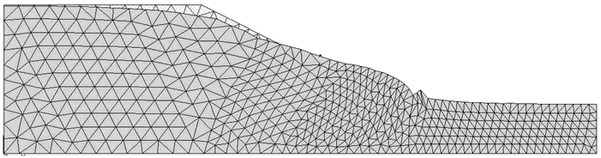
Fig. 49. Mesh deformata
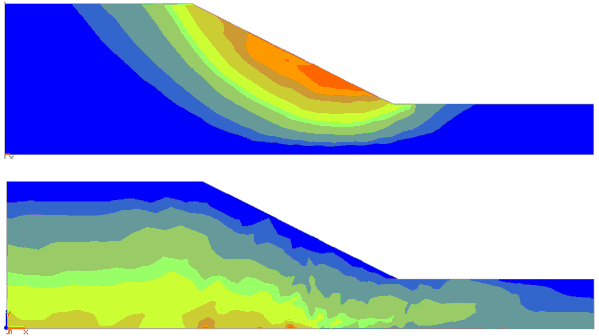
Fig. 50. Spostamenti totali e tensioni di Von Mises.
Confronto con i Metodi dell’Equilibrio Limite
Per avvalorari i risultati raggiunti con l’analisi di stabilità, eseguita con i Metodi numerici ad Elementi Finiti (FEM), è di seguito confrontata con i classici Metodi dell’Equilibrio Limite (LEM) di Bishop e di Morgenstern.
I risultati raggiunti, con entrambi i metodi, hanno condotto ad un valore del fattore di sicurezza pari ad 1.61, perciò del tutto simile a quello raggiunto con i metodi FEM.
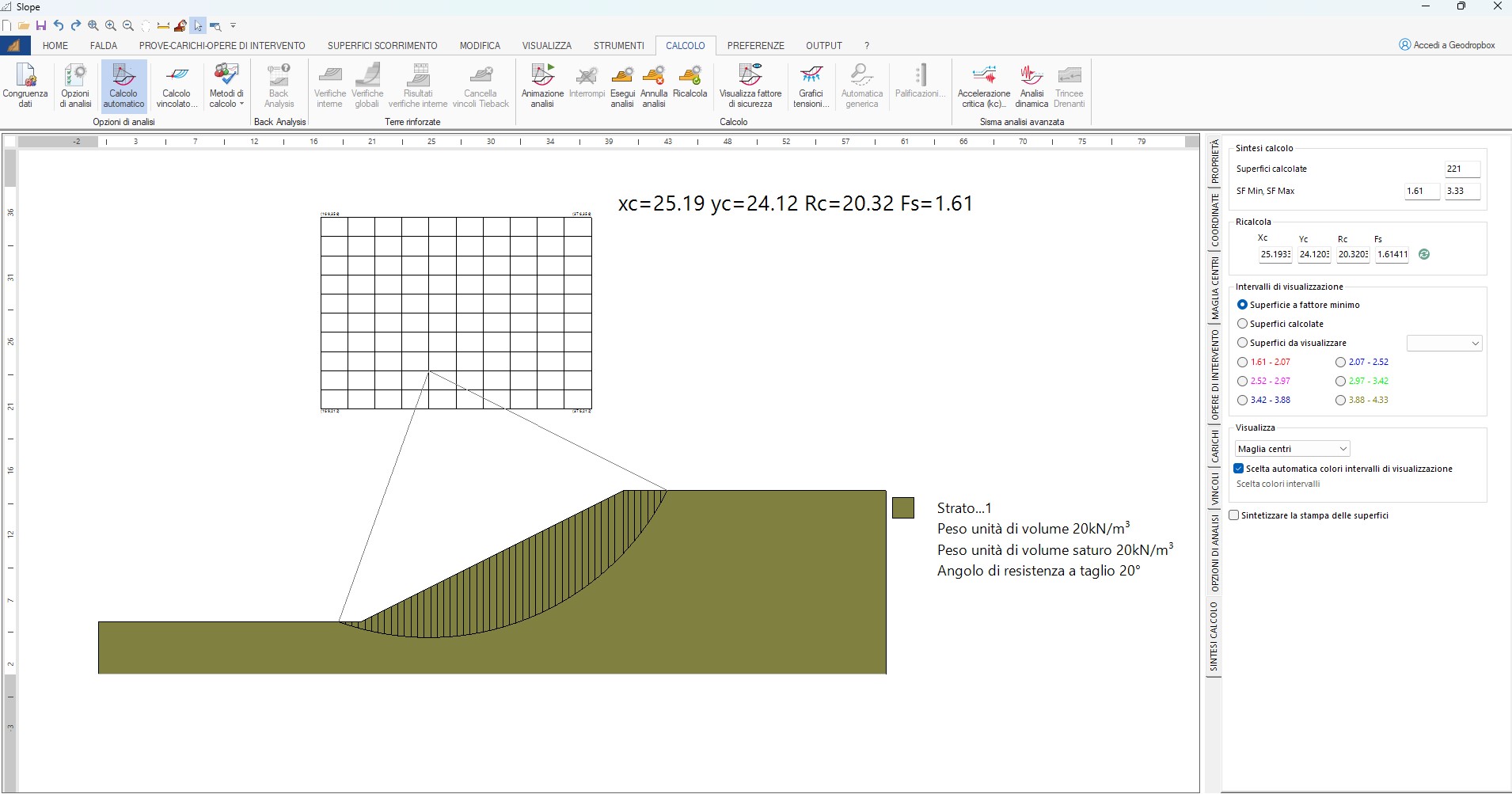
Fig. 51. Simulazione effettuata in Slope con i Metodi di Bishop e Morgenstern