Si considera un elemento chiodo collegato in un qualsiasi punto del bordo di un elemento piano a 4 nodi (Figura 30).
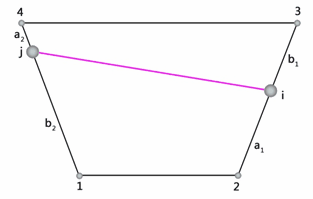
Fig. 30. Chiodo connesso ad un elemento piano
La relazione deformazione-rigidezza per i chiodi può essere scritta come:
Dove k’, u’ e r’ rappresentano rispettivamente la matrice delle rigidezze, il vettore spostamento e il vettore forze nodali associati ai gradi di libertà dei nodi i e j dell’elemento chiodo.
Il vettore spostamento è definito come:
Con gli spostamenti interpolati linearmente lungo i bordi del quadrilatero, la trasformazione del vettore spostamento dei nodi dell’elemento chiodo u’è dato dalla matrice di trasformazione T e dal vettore spostamento dei nodi dell’elemento piano u, come:
Dove la matrice di trasformazione T contiene termini come quelli riportati nell’Equazione 108. Per il caso descritto nella Figura 30 la relazione di trasformazione degli spostamenti può essere espressa in forma matriciale come segue:
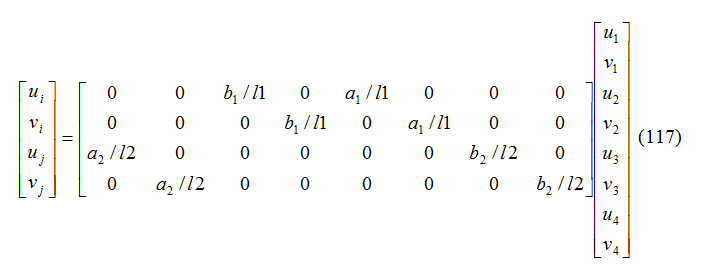
In seguito alla trasformazione, k’ e r’ dell’elemento chiodo devono essere convertite in k e r a cui sono associati tramite i gradi di libertà dei 4 nodi dei vertici dell’elemento quadrangolare.
Così, 
diventa 
e 
diventa 
.
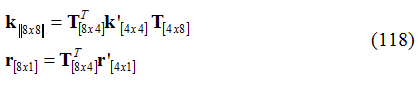
Solo ora è quindi possibile sommare il vettore forza nodale e la matrice delle rigidezze ai corrispondenti vettori dell’elemento quadrangolare o assemblati nella struttura. I nodi i e j del chiodo e i suoi gradi di libertà non sono esplicitamente presenti. Si può dire che i gradi di libertà della barra sono costretti a seguire i gradi di libertà del quadrilatero.
Una relazione simile si può ottenere nel caso in cui il chiodo è collocato all’interno di un elemento piano di ordine superiore. In questo caso gli spostamenti nodali del chiodo sono interpolati quadraticamente dai gradi di libertà traslazionali dei nodi dell’elemento piano.
Ad esempio assumendo un elemento di ordine superiore quadrangolare ad 8 nodi, attraversato da un elemento chiodo, la relazione di trasformazione dello spostamento è:
In cui:
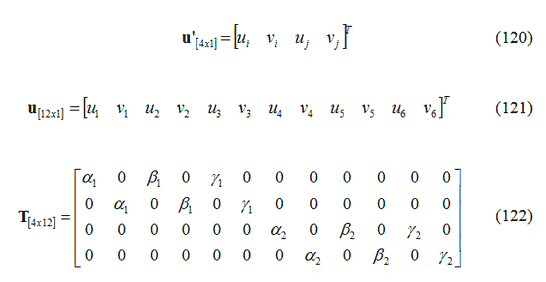
Dove:
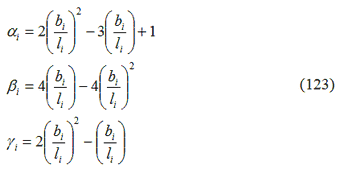
Questo approccio può sempre essere applicato quando i nodi dei chiodi ricadono all’interno dell’elemento piano.
Considerando invece un chiodo con i nodi i e j ricadenti nell’elemento triangolare a 3 nodi come mostrato nella Figura 31:
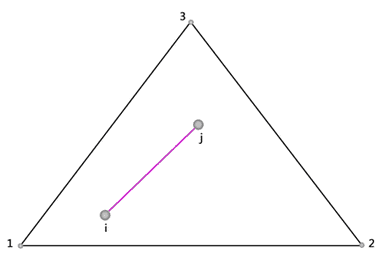
Fig. 31-Chiodo all’interno di un elemento piano triangolare.
gli spostamenti degli elementi nodali si possono ottenere attraverso le funzioni di forma degli elementi “genitori” come:
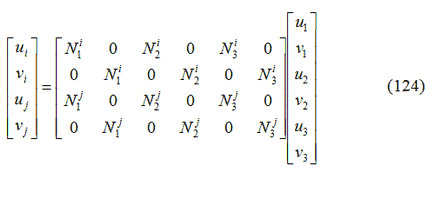
Dove 
, k=1,2,3 rappresenta le funzioni di forma per l’elemento triangolare stimate per ogni coordinata dei nodi del chiodo.
Quindi la matrice delle rigidezze e il vettore forze nodali si ottengono nel seguente modo:
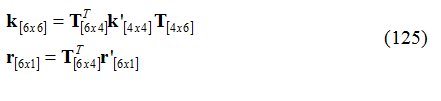
Dove la matrice di trasformazione è:
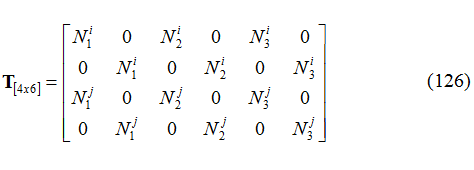
Matrici di trasformazione simili si possono ottenere tutte le volte che si utilizzano elementi di forma quadrangolare oppure elementi piani di ordine superiore. Le funzioni di forma sono valutate nei nodi dell’elemento chiodo di coordinate note.
Di solito queste coordinate sono fornite in coordinate globali laddove le funzioni di forma degli elementi piani sono date nel sistema di coordinate naturali. Pertanto sono necessarie alcune trasformazioni per ottenere le coordinate dei nodi del chiodo nel sistema di coordinate naturali.
Queste trasformazioni si basano sul carattere isotropo dell’elemento piano utilizzato. Per gli elementi triangolari le coordinate globali (x,y) e le coordinate naturali (ξ,η) sono messe in relazione come segue:
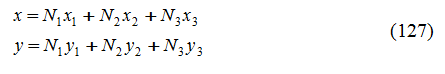
In cui xi, yi (i=1,2,3) rappresentano le coordinate dei nodi dell’elemento triangolare e la funzione di forma Ni ha la seguente espressione, rappresentata nel sistema di coordinate naturali:
Per le coordinate note x y si possono ricavare le corrispondenti coordinate naturali risolvendo il seguente sistema di equazioni:
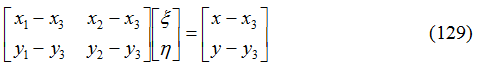
In maniera del tutto simile si possono ottenere le coordinate naturali nel caso in cui l’elemento piano è rappresentato da un elemento quadrangolare.