Si assume che gli incrementi di deformazione includano componenti sia elastiche sia plastiche e che tali incrementi siano molto piccoli. È possibile determinare una relazione incrementale tensione-deformazione analoga alla relazione di elasticità ![]() .
.
Durante un incremento della deformazione plastica, dF=0 e così:
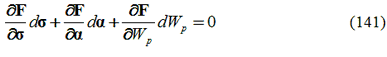
Per sostituzione:
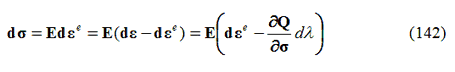
L’equazione risultante da risolvere per ottenere il moltiplicatore plastico è:
![]()
dove Pλ è un vettore in cui sono inclusi sia il lavoro di incrudimento sia il lavoro di deformazione come segue:
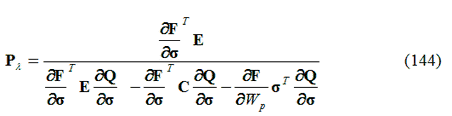
Per cui riordinando i termini si ha:
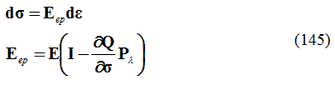
Dove I è una matrice unitaria e Eep è la matrice costitutiva tangente generalizzata.
Se Q=F (in aggiunta alla legge del flusso), la matrice Eep risulta simmetrica. Per F<0 (non si verifica lo snervamento) o per F=0 e dF<0 (fase di scarico dello stato plastico) allora Eep è pari a E.
La matrice delle rigidezze tangente kt è data dall’Equazione 146:
