L’analisi a capacità portante si esegue a partire dalla condizione di deformazione piana e, al fine di visualizzare il comportamento elasto-plastico, i carichi sono aumentati in modo incrementale finché non si verifica il collasso. Il metodo effettua le iterazioni a rigidezza costante (metodo di Newton Raphson modificato), cosicché il processo di fattorizzazione della matrice delle rigidezze è richiamato una sola volta nel programma, mentre la fase di sostituzione all’indietro viene richiamata in ciascuna iterazione. Diversi criteri di rottura sono stati implementati per rappresentare la resistenza dei terreni: nel caso di terreni dotati di attrito e coesione alla resistenza al taglio è appropriato l’utilizzo del criterio di Mohr Coulomb. Per argille non drenate, senza attrito, invece, occorre utilizzare il criterio di Von-Mises.
L’esempio mostrato nella Figura 58 rappresenta una fondazione poggiante sulla superficie di uno strato di argille uniformi non drenate. Il terreno sottostante sostiene una tensione uniforme q, che viene aumentata in modo incrementale fintanto che si giunge a rottura. Il legame costitutivo del terreno è elasto-plastico definito, nella fase plastica, dal criterio di rottura di Von Mises attraverso tre parametri: il valore della coesione non drenata Cu e le proprietà elastiche del mezzo E e ν. I carichi generano una tensione uniforme pari a 1kN/m2 nel piano di semi-ampiezza pari a 4 m.
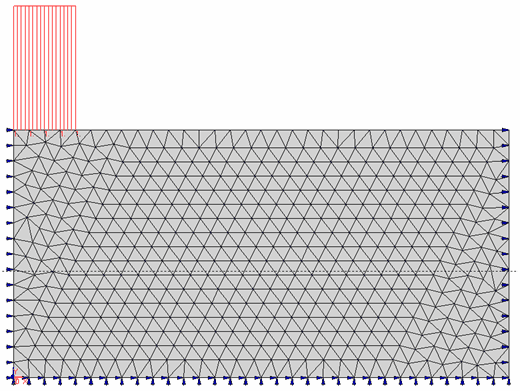
Fig. 62. Mesh dell’esempio di analisi a capacità portante.

Tabella 10. Proprietà dei materiali
Nella Tabella 11 di seguito, sono stati riportati i valori restituiti dall’analisi a capacità portante eseguita: si vede chiaramente che, per un valore del Fattore di Carico di circa 382 si ottiene uno spostamento che si aggira sui 2.5 cm. Come noto dalla pratica ingegneristica, si può assumere il valore di 2.5 cm come sintomatico della rottura del materiale di cui è costituita la sezione, nonostante il calcolo non abbia fallito la convergenza.
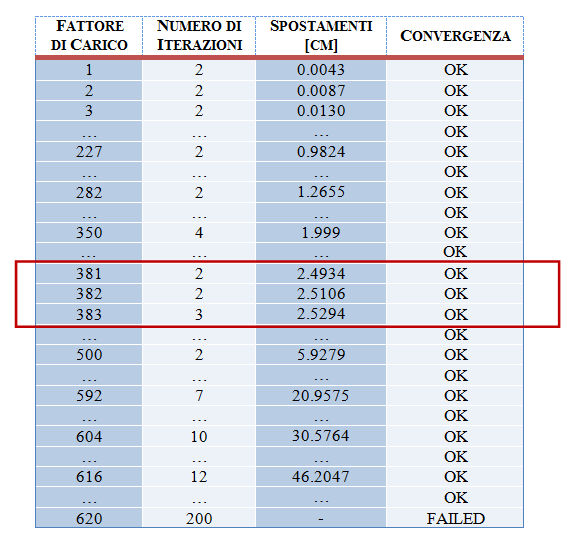
Tabella 11. Sintesi dei risultati ottenuti dall’analisi a capacità portante
I carichi sono fattorizzati incrementando il coefficiente di carico da 0.1 ad 1, che corrisponde alla rottura. Ai livelli di carico inferiori a quello di rottura la convergenza si verifica in tempi relativamente brevi e con poche iterazioni. Al collasso, l’algoritmo lavora “di più” e pertanto il calcolo richiede molte più iterazioni.
Al termine dell’analisi GFAS consente di visualizzare la sezione deformata, gli spostamenti in direzione y, gli spostamenti totali e le tensioni xy (Figure 63, 64, 65, 66).

Fig. 63. Mesh deformata

Fig. 64. Spostamenti in direzione y

Fig. 65. Spostamenti totali
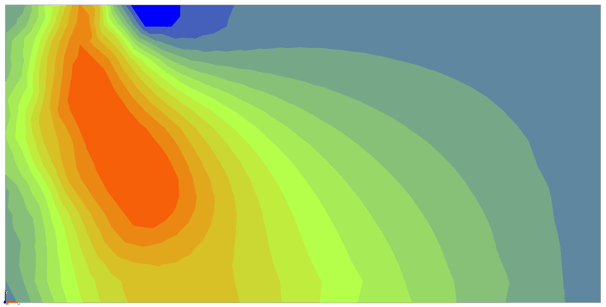
Fig. 66. Sigma XY