L’equazione differenziale parziale che governa il fenomeno stazionario per un acquifero confinato nel piano orizzontale (x,y) è:
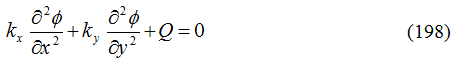
dove ϕ è il potenziale del fluido o prevalenza totale misurata dal fondo dell’acquifero, kx e ky sono i coefficienti di permeabilità nella direzione x e y, e Q è il valore della portata di ricarica. Il pompaggio fornisce un valore negativo di Q.
Il carico totale ϕ del fluido in un punto è dato dalla seguente espressione:
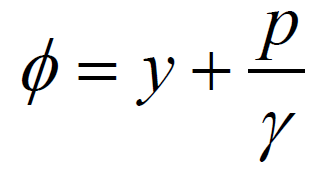(198.1)
Dove y è la quota del punto considerato, p è la pressione del fluido e γ il peso di volume del fluido considerato.
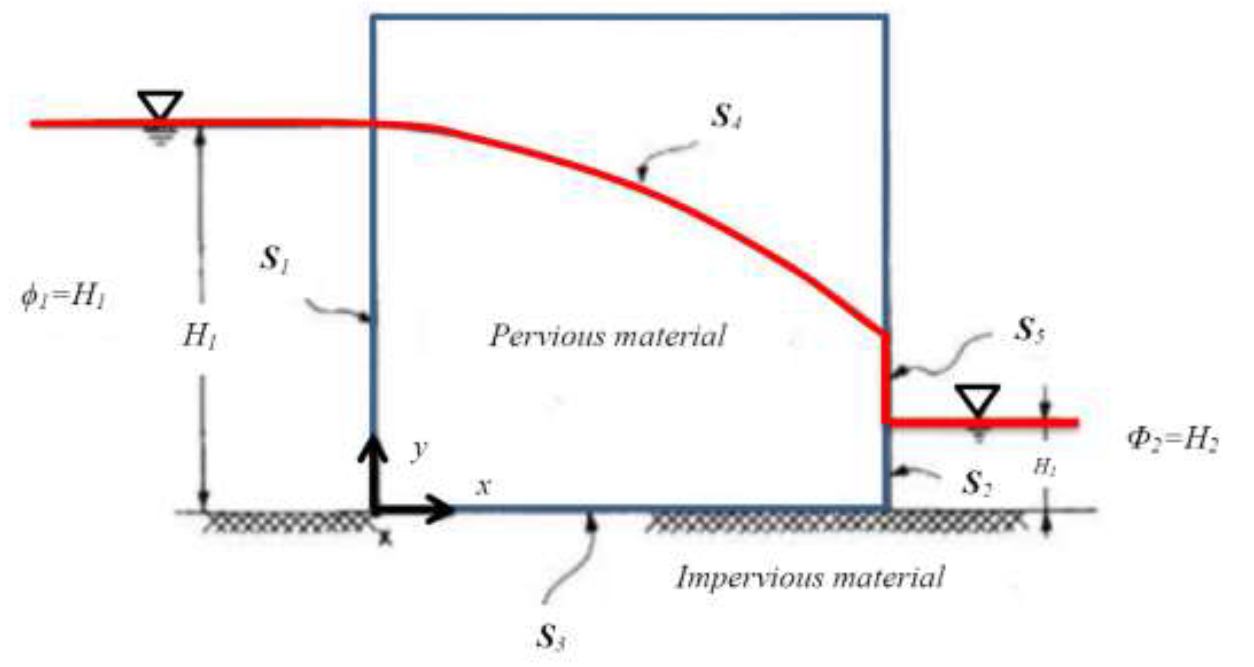
Figura (a)-Flusso non confinato, analisi stato stazionario. Condizioni al contorno.
In un problema di flusso stazionario come rappresentato in figura (a) l'esatta posizione e localizzazione dei contorni S4 e S5 non sono note, anche se si conoscono le condizioni al contorno. La superficie S4 è caratterizzata da pressione nei pori nulla lungo la superficie e prevalenza totale uguale alla quota y.
Le condizioni al contorno sono:
- per le superfici a monte e a valle:
ϕ = ϕ1 su S1
ϕ = ϕ2 su S2
- per la superficie di base impermeabile S3:
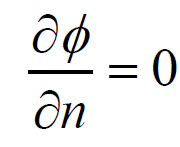
dove n è la normale alla superficie;
- per la superficie libera S4
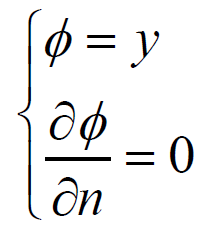
- per la superficie libera S4
ϕ = y su S4
Il processo di discretizzazione ad elementi finiti riduce l’equazione differenziale (198) in un insieme di equazioni di equilibrio nella forma:
dove kc è la matrice simmetrica di permeabillità, Φ è il vettore nodale del potenziale (carico totale), e q è un vettore nodale afflussi/deflussi.
Gli elementi della matrice sono calcolati utilizzando l’Equazione 200:
assumendo che gli assi principali del tensore di permeabilità coincidano con gli assi x ed y.
La matrice K è data da:
mentre la matrice T, data dall’Equazione 202, è la matrice di interpolazione del gradiente potenziale totale dell'elemento: assume lo stesso significato della matrice B deformazione-spostamento.
Ad esempio per un elemento quadrilatero a 4 nodi, la matrice T è data da:
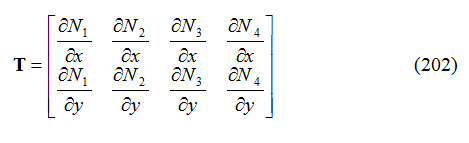
Per imporre le prevalenze totali assegnate sui bordi si aggiungono coefficienti di permeabilità elevati agli elementi diagonali di Kc corrispondenti ai nodi al contorno, e si specificano le condizioni di flusso che risultano dai potenziali totali dati. Quindi l'equazione (199) viene modificata per ottenere:
(kc + kb)Φ=Qb (199.1)
dove kb è una matrice diagonale, l'elemento i-esimo della diagonale è uguale a zero se il carico ϕi non è assegnato, altrimenti è uguale a k, dove k>>kii (di solito si assegna un grande valore di penalità in GFAS nel pannello Analisi flusso in regime stazionario). Conseguentemente, l'i-esimo elemento del vettore Q è uguale a zero se ϕi non è specificato, altrimenti è uguale a kϕi .
La soluzione al problema delle infiltrazioni potrebbe essere ottenuta subito se fosse nota la superficie libera S4. Verrebbe effettuata la discretizzazione ad elementi finiti del dominio entro i confini Si (i=1…5), e i potenziali totali incogniti nei punti nodali potrebbero essere risolti utilizzando l'equazione (199.1). Tuttavia, con la posizione S4 sconosciuta, è pratica comune assumere una superficie libera, risolvere l'equazione (199.1) con non tutte le condizioni al contorno imposte, controllare se tutte le condizioni al contorno sono soddisfatte e iterare con la superficie libera S4 fino a quando non è stata trovata una soluzione che soddisfa tutte le condizioni al contorno. Il requisito di base nella soluzione di iterazione della mesh ad elementi finiti di cui sopra è che non ci deve essere flusso al di sopra della linea ϕ=y. Per la risoluzione del problema viene eseguita una discretizzazione ad elementi fini in cui la permeabilità è considerata:
a) k, per ϕ≥ y
b) 0, per ϕ< y
La permeabilità del materiale di cui soopra corrisponde ad una permeabilità non lineareche viene trattata in due modi differenti: 1) Nonlinear air element e 2)True air elements.
Nel caso 1) la permeabilità è impostata ad un valore molto basso per gli elementi che si trovano sopra la superficie freatica e per tutti i nodi dell'elemento.
Nel caso 2) la permeabilità è imposta a zero per gli elementi che si trovano sopra la superficie freatica e per tutti i nodi dell'elemento.