Le equazioni che governano la risposta dinamica della massa si ricavano imponendo che il lavoro compiuto dalle forze esterne venga assorbito dal lavoro delle forze interne, inerziali e viscose per ogni piccolo movimento cinematicamente ammissibile. Per un singolo elemento si può scrivere:
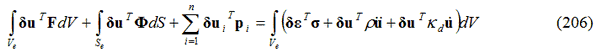
dove:
δu - vettore dei piccoli spostamenti arbitrari
δε - vettore delle piccole deformazioni arbitrarie
F - vettore delle forze di volume
Φ- trazioni superficiali vincolate
Pi - vettore dei carichi concentrati
δuTi - spostamento del nodo su cui è applicato il carico Pi
ρ - densità del materiale
Kd -parametro di smorzamento del materiale
Chiamando con N le funzioni di forma degli elementi finiti, si ha un campo degli spostamenti u e le sue derivate (campi di velocità e accelerazione):

dove il vettore d contiene gli spostamenti ai nodi degli elementi finiti che saranno solo funzioni del tempo.
Combinando le Equazioni 206 e 207 e tenendo conto che gli spostamenti δu sono arbitrari, si ottengono le seguenti coppie di equazioni ordinarie differenziali del secondo ordine funzioni del tempo:
![]()
dove la matrice di massa degli elementi e la matrice di smorzamento sono definite come:

I vettori delle forze interne e dei carichi esterni si ottengono come:
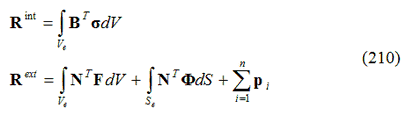
Il vettore dei gradi di libertà, per una struttura libera di oscillare, ovvero sottoposta ad un moto armonico per cui ciascun grado di libertà di muove in fase con gli altri, è definito come:
![]()
Combinando le Equazioni 208 e 211 e ponendo che C=0 e Rext=0 si ottiene:

Che rappresenta lo stato basilare dei problemi di vibrazione, in cui K rappresenta la matrice delle rigidezze della struttura ed M la matrice di massa globale che può essere “lumped” o “consistent”.
Gli elementi della matrice di massa “consistent” si ottengono dalla seguente relazione:

dove N rappresenta la matrice delle funzioni di forma.
La matrice “lumped” invece si ottiene inserendo la massa mi delle particelle ai nodi di ogni elemento in modo tale che ![]() sia la massa totale dell’elemento. Inoltre, una matrice “lumped” è diagonale, a differenza della matrice “consistent”. Per un elemento quadrilatero a 4 nodi, per esempio, la matrice “lumped” è data da:
sia la massa totale dell’elemento. Inoltre, una matrice “lumped” è diagonale, a differenza della matrice “consistent”. Per un elemento quadrilatero a 4 nodi, per esempio, la matrice “lumped” è data da:
![]()
dove A rappresenta l’area dell’elemento ed I la matrice unitaria.