Questo tipo di elemento è rappresentato da un elemento chiodo deformabile che comporta come un singolo elemento e l’interazione con la mesh di elementi finiti avviene soltanto attraverso il punto finale dell’elemento.
Questi elementi si possono assegnare dovunque nel reticolo e sono quindi rappresentati nella mesh (Figura 33). La matrice delle rigidezze degli ancoraggi è sommata alla matrice delle rigidezze della struttura come si mostra in questa sezione.
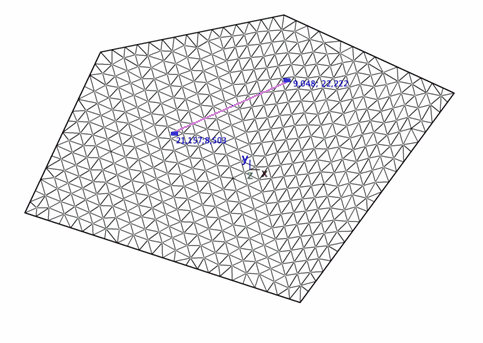
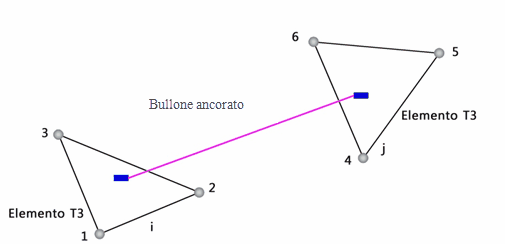
Fig. 33. Bullone ancorato all’estremità.
I gradi di libertà degli elementi ancorati sono calcolati in funzione degli spostamenti nodali dell’elemento piano in cui i nodi finali di ancoraggio ricadono:
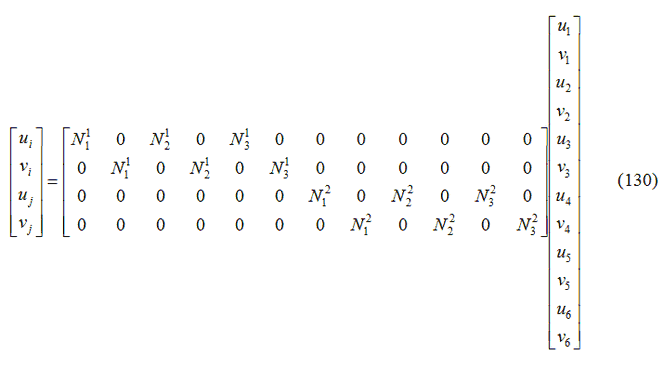
Oppure in forma compatta:
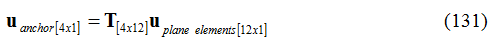
In seguito, la matrice delle rigidezze dell’ancoraggio e il vettore delle forze nodali sono così valutati:
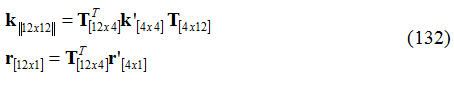
Eseguita questa trasformazione, il vettore delle forze nodali e la matrice delle rigidezze possono essere direttamente sommati ai corrispondenti matrice e vettore degli elementi piani “genitori” oppure assemblati nella struttura.
I nodi i e j dell’elemento ‘bullone’ e i suoi gradi di libertà non sono esplicitamente presenti, si può dire infatti che i gradi di libertà della barra sono vincolati in modo da seguire i gradi di libertà degli elementi piani “genitore”. Anche gli altri casi legati agli elementi di ordine superiore oppure ad elementi quadrangolari possono essere considerati allo stesso modo.
La forza assiale F nell’ancoraggio è calcolata dalla relazione che lega la rigidezza con lo spostamento espressa nel sistema locale come:
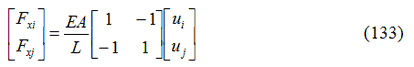
In cui gli spostamenti ai nodi i e j sono calcolati in funzione degli spostamenti nodali degli elementi piani “genitori” attraverso le funzioni di forma.
Ad esempio, considerando un elemento triangolare a 3 nodi (Figura 33) gli spostamenti in ogni nodo, nel sistema di coordinate globale, sono espressi come:
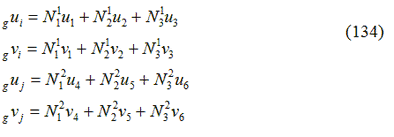
Dove Nik rappresenta le funzioni di forma calcolate per ciascun elemento piano associato all’elemento con l’estremità ancorata.
Questi spostamenti sono trasformati nel sistema di coordinate locali tramite la matrice di trasformazione (Equazione 131) come:

In ultimo, con gli spostamenti assiali locali calcolati utilizzando le equazioni scritte sopra, le forze assiali lungo l’ancoraggio si determinano usando l’Equazione 133.
Nel programma sono stati implementati gli ancoraggi con comportamento lineare e elasto-plastico.
Nel primo caso l’ancoraggio ha un comportamento elastico e la rottura non avviene. Nel secondo caso, la rottura dell’elemento è funzione della resistenza a trazione del materiale del bullone (Figura 34). Quando la forza assiale nell’elemento raggiunge lo snervamento, l’elemento si considera rotto e non interviene nessuna resistenza residua.
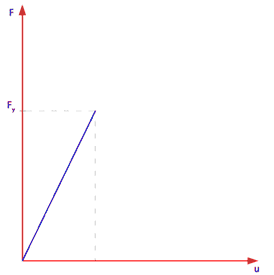
Fig.34. Criterio di rottura.