La relazione di rigidezza dell’elemento trave-pilastro è:
![]()
Dove i vettori spostamento e carico nodale sono definiti:
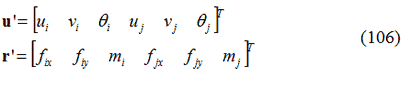
Si assume che gli spostamenti traslazionali ai nodi i dell’elemento trave-pilastro siano interpolati linearmente lungo il tratto 2-3 dai gradi di libertà traslazionali dei nodi 2 e 3 dell’elemento piano e che la rotazione θi sia la stessa di quella del lato 2-3.
In queste condizioni gli spostamenti nodali possono essere scritti come:
![]()
Dove, con c=cos β e s=sin β.
La matrice T di trasformazione è:
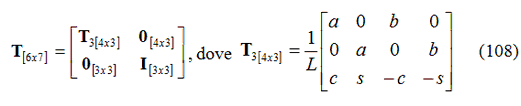
mentre il vettore spostamento u, che contiene gli spostamenti dell’elemento piano e gli spostamenti dei nodi liberi j dell’elemento trave-pilastro, è:
![]()
Applicando il principio degli spostamenti virtuali, se tra gli spostamenti u e u’ vale la relazione 107, allora per i vettori forza nodale r ed r’ si può scrivere una relazione simile:
![]()
Si può dimostrare che, dato che r e r’ descrivono la stessa risultante delle forze, il lavoro compiuto dalle forze durante uno spostamento virtuale stabilito deve essere indipendente dal sistema di coordinate in cui il lavoro viene calcolato. In queste condizioni, moltiplicando entrambi i termini dell’Equazione 105 per TT e sfruttando l’Equazione 107 per calcolare il vettore spostamento u’, l’Equazione 105 diventa:
![]()
che in forma compatta è:
![]()
Dove la matrice delle rigidezze modificata relativa all’elemento trave-pilastro è:
![]()
A questo punto l’elemento piano e l’elemento trave-pilastro possono essere assemblati l’uno con l’altro o assemblati al resto della struttura. Il nodo i e i suoi gradi di libertà non appaiono nelle strutture assemblate. Il nodo i può essere definito nodo “slave” perché i suoi gradi di libertà sono completamente determinati dai gradi di libertà dei nodi “master” 2 e 3. Una relazione simile si può ottenere nel caso in cui l’elemento trave-pilastro è collocato all’interno di un elemento piano di ordine superiore. In questo caso gli spostamenti nodali dell’elemento trave sono interpolati attraverso una funzione quadratica dai gradi di libertà traslazionali dei nodi dell’elemento piano.