Risolvere un problema agli elementi finiti consiste nel valutare i singoli elementi che compongono le matrici di rigidezza e i vettori, per poi assemblarli in un’unica matrice delle rigidezze globale e nei vettori forza. L’insieme delle equazioni simultanee, che in questo modo si generano, sono successivamente risolte per determinare gli spostamenti nodali.
Si definiscono σ ed ε i vettori contenenti, rispettivamente, le sei componenti di sollecitazione e di deformazione:
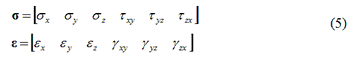
Il legame tensione-deformazione assume la forma:
![]()
oppure:
![]()
dove E è una matrice simmetrica definita positiva, di costanti elastiche e C la sua inversa (C=E-1).
Le componenti del vettore spostamento u lungo le direzioni x, y, e z sono rispettivamente u, v e w. La convenzione dei segni è la seguente: si assumono positivi gli spostamenti e le forze concordi con gli assi coordinati rappresentati in Figura 14.
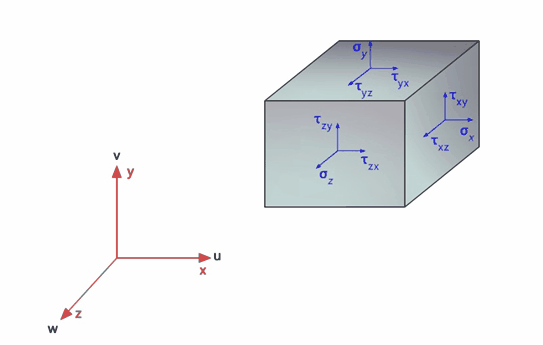
Fig. 14. Componenti delle tensioni.