Il primo approccio si sviluppa con iterazioni a rigidezze costanti in cui la non-linearità è introdotta modificando iterativamente il vettore dei carichi. La matrice delle rigidezze globale, di solito elastica, in tale analisi viene formata una sola volta. Ciascuna iterazione, in questo modo, rappresenta un’analisi elastica. La convergenza si ottiene quando le tensioni generate dai carichi soddisfano la legge tensione-deformazione o il criterio di rottura ipotizzato, rispettando una prefissata tolleranza. Il vettore dei carichi, in ogni iterazione, è determinato dall’applicazione dei carichi esterni e dai carichi auto-equilibranti. I carichi di volume hanno l’effetto di ridistribuire le tensioni (o i momenti) nel sistema, senza alterare il carico netto. Il metodo è mostrato nella Figura 42. Per problemi con carico-controllato, quanto più ci si avvicina alla rottura, maggiore sarà il numero di iterazioni richieste, perché la matrice delle rigidezze globale elastica inizia a sovrastimare la rigidezza reale del materiale.
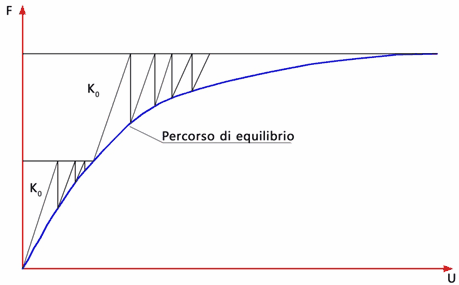
Fig. 42. Metodo a rigidezze costanti
Gli effetti delle azioni plastiche possono essere considerati come le tensioni iniziali che produrrebbe un carico fittizio combinate con quelle del carico realmente applicato. Questa procedura evita che le fasi onerose di calcolo, come la formazione e la fattorizzazione della matrice delle rigidezze tangente, siano effettuate ripetutamente, ma la convergenza si presenta tanto più lenta quanto maggiori saranno le deformazioni plastiche.