Il secondo approccio, mostrato nella Figura 43, prende in considerazione la riduzione della rigidezza del materiale.
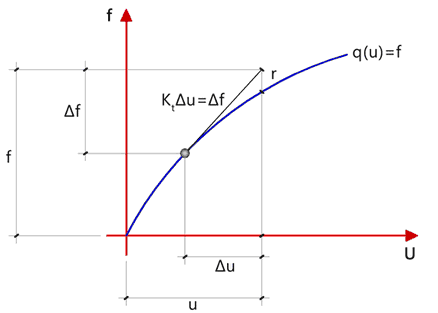
Fig. 43. Step di carico nel metodo a rigidezza tangente.
Se si considerano step di carico abbastanza piccoli, il metodo diventa equivalente al metodo esplicito di Eulero. Secondo questo approccio la matrice delle rigidezze globale deve essere aggiornata periodicamente e le iterazioni per raggiungere la convergenza si effettuano utilizzando i carichi di volume residuali.
Contrariamente a quanto avviene con l’approccio a rigidezza costante, l’onere aggiuntivo di ri-formare e ri-fattorizzare la matrice delle rigidezze globale nel metodo di rigidezza variabile, è compensato dalla riduzione del numero di iterazioni necessarie che diminuisce quanto più si è vicini alla rottura.
L’algoritmo richiede che la rappresentazione della relazione tra tensioni-deformazioni debba essere memorizzata, cosicché le tensioni e le costanti elastiche possano essere ricavate per ogni deformazione. Si devono inoltre memorizzare ed aggiornare, per ogni punto di campionamento di ciascun elemento e dopo ogni ciclo di calcolo, le deformazioni, le tensioni e gli spostamenti nodali.
E’ pertanto necessaria una relazione incrementale tra spostamenti e forze:

dove Kt è la matrice delle rigidezze tangente e l’equazione sopra riportata rappresenta la forma linearizzata dell’equazione non lineare (Equazione 185):

Il calcolo procede con l’applicazione di un incremento di carico ∆F e con il calcolo del corrispondente incremento dello spostamento con l’Equazione 184 (Figura 43). L’incremento della deformazione è valutata nel solito modo, cioè:
![]()
Successivamente le tensioni vengono calcolate con la relazione costitutiva elasto-plastica:
![]()
Questa rappresenta una relazione non lineare fintanto che la matrice Eep dipende dallo stato tensionale corrente e la procedura iterativa generale può così essere utilizzata. Sulla base, quindi, del calcolo delle tensioni, il vettore delle forze interne Q può essere valutato risolvendo l’integrale seguente:

che deve essere bilanciato dal carico totale applicato F, pertanto, la forza residua svanisce:
![]()
Se il valore della forza residua è diverso dalla tolleranza prefissata, vuol dire che è applicata come un carico esterno seguendo la procedura di Newton-Raphson. Questa forza residua offre un nuovo incremento della deformazione e un corrispondente nuovo incremento della tensione, che deve essere determinato tramite la relazione costitutiva elasto-plastica non lineare, calcolando successivamente un nuovo valore residuale e così via finché il valore residuo non diventi sufficientemente piccolo.
La procedura può essere schematizzata come segue:
1.Si applica l’incremento di carico ∆F e si trovano i valori degli incrementi dello spostamento e della deformazione, rispettivamente ∆u e ∆ε.
2.Si determina l’incremento di tensione ∆σ dall’equazione (187).
3.Si calcola il valore residuo R.
4.Se ||R||< tol si ricava kt e si ritorna allo step 1.
Così, il calcolo di uno step di carico richiede una procedura iterativa globale dove le forze non bilanciate, anche dette residuali, devono svanire, così come prevede la procedura al fine di calcolare gli incrementi delle tensioni (step 2). L’aggiornamento delle tensioni si effettua in ogni punto di integrazione. Per calcolare l’incremento delle tensioni causato dall’incremento delle deformazioni, nel codice è, quindi, implementato lo schema di integrazione all’indietro.
Essenzialmente il metodo consiste nell’applicazione di predittore elastico seguito da un correttore plastico, al fine di garantire che la tensione finale sia quasi sulla superficie di rottura.