Il moto permanente gradualmente variato è quello che si verifica in una corrente a pelo libero con variazioni graduali della sezione. Naturalmente la condizione di continuità impone che la portata rimanga costante, mentre velocità e sezione variano gradualmente lungo l’asse s della corrente.
Si consideri una corrente in moto permanente con piccola pendenza e portata Q costante. Isolando un tronco d’alveo di lunghezza ds (con s ascissa misurata a partire da un’origine arbitraria, in direzione orizzontale e verso coincidente con quello del moto) il fondo si abbassa di if ds e la linea dei carichi totali di Jds, avendo indicato con J la cadente.
Da semplici considerazioni geometriche si ha:

L’espressione b), in cui per semplicità if è stato posto pari ad i, indica chiaramente che l’energia specifica totale rispetto al fondo, aumenta per l’abbassamento del fondo stesso e diminuisce per effetto delle resistenze.
Sostituendo ai differenziali gli incrementi finiti, la b) diventa:
![]()
Poiché la E risulta funzione di s tramite l’altezza h, si ha:
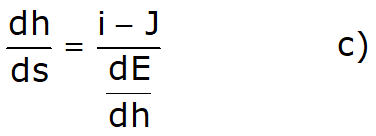
Dall’andamento della E in funzione di h, sappiamo che la E decresce al crescere di h (dE/dh < 0) per le correnti veloci (h < k), ed è crescente (dE/dh > 0) per le correnti lente (h > k); in corrispondenza dello stato critico dE/dh = 0.
Infine, accettando per la perdita di carico J la seguente espressione:
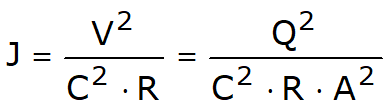
si ricava che la J è tanto più piccola quanto maggiore è h, dato che tutti i termini del denominatore crescono con h, e si può concludere che il numeratore della c) risulta positivo (i > J) per altezze d’acqua superiori a quelle di moto uniforme (h > h0), negativo per altezze d’acqua inferiori a quelle di moto uniforme (h < h0).
Le considerazioni fatte finora sono alla base di quello che sarà il possibile andamento dei profili dell’acqua: osserviamo in generale che, quando l’altezza dell’acqua si accosta a quella di moto uniforme, la dh/ds tende a zero, ossia il profilo tende a disporsi parallelo al fondo e quindi a quello di moto uniforme.
Per contro, quando l’altezza si avvicina al valore critico k, la dE/dh tente ad annullarsi e pertanto il profilo tende a disporsi perpendicolarmente al fondo.
I profili di moto permanente sono dunque descritti analiticamente dall’espressione b), pertanto definiti a meno di una costante arbitraria da determinare fissando in una sezione l’altezza h = h*.
Tale condizione va ricercata in corrispondenza di una causa perturbatrice che provoca, in una sezione, un’altezza h diversa da quella di moto uniforme; si ricorda a tale proposito che la casusa perturbatrice può esercitare la sua influenza verso monte solo se la corrente è lenta (o lo diventa), può esercitarla verso valle soltanto se la corrente è veloce (o lo diventa per sua causa).
Tutto ciò porta a stabilire che la condizione al contorno per risolvere l’equazione del profilo, e quindi il punto di partenza del tracciamento, va ricercata a valle se la corrente è lenta, a monte se la corrente è veloce.
In tale sezione dovrà quindi ritenersi nota l’altezza h* determinata dalla causa perturbatrice e quindi sarà noto il dislivello h*- h0 rispetto al moto uniforme.
|
© GeoStru