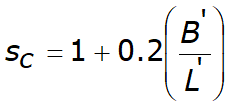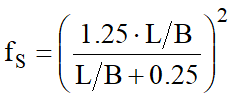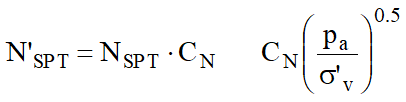La carga última de una cimentación superficial se puede definir como el valor máximo de la carga con el cual en ningún punto del subsuelo se alcanza la condición de rotura (método de Frolich), o también como aquel valor de carga, mayor que el anterior, con el cual el fenómeno de rotura se extiende a un amplio volumen del suelo (método de Prandtl y sucesivos).

 

Observaciones experimentales han demostrado que la rotura se puede dar por medio de tres mecanismos (véase Fig. 4.5.1):

La rotura general que se caracteriza por la formación de superficies de deslizamiento bien definidas. Parte desde la cimentación hasta el plano del terreno y hace que el terreno presente levantamientos a los lados de la cimentación.La rotura por punzonamiento, con la cual el hundimiento de la cimentación se debe a la formación de planos de corte verticales, a lo largo del perímetro, sin generar superficies de deslizamiento.

La rotura local corresponde siempre a la formación de una clara superficie de deslizamiento bajo la cimentación que sin embargo se dispersa en el suelo adyacente. Se nota una modesta tendencia al levantamiento del terreno.

 

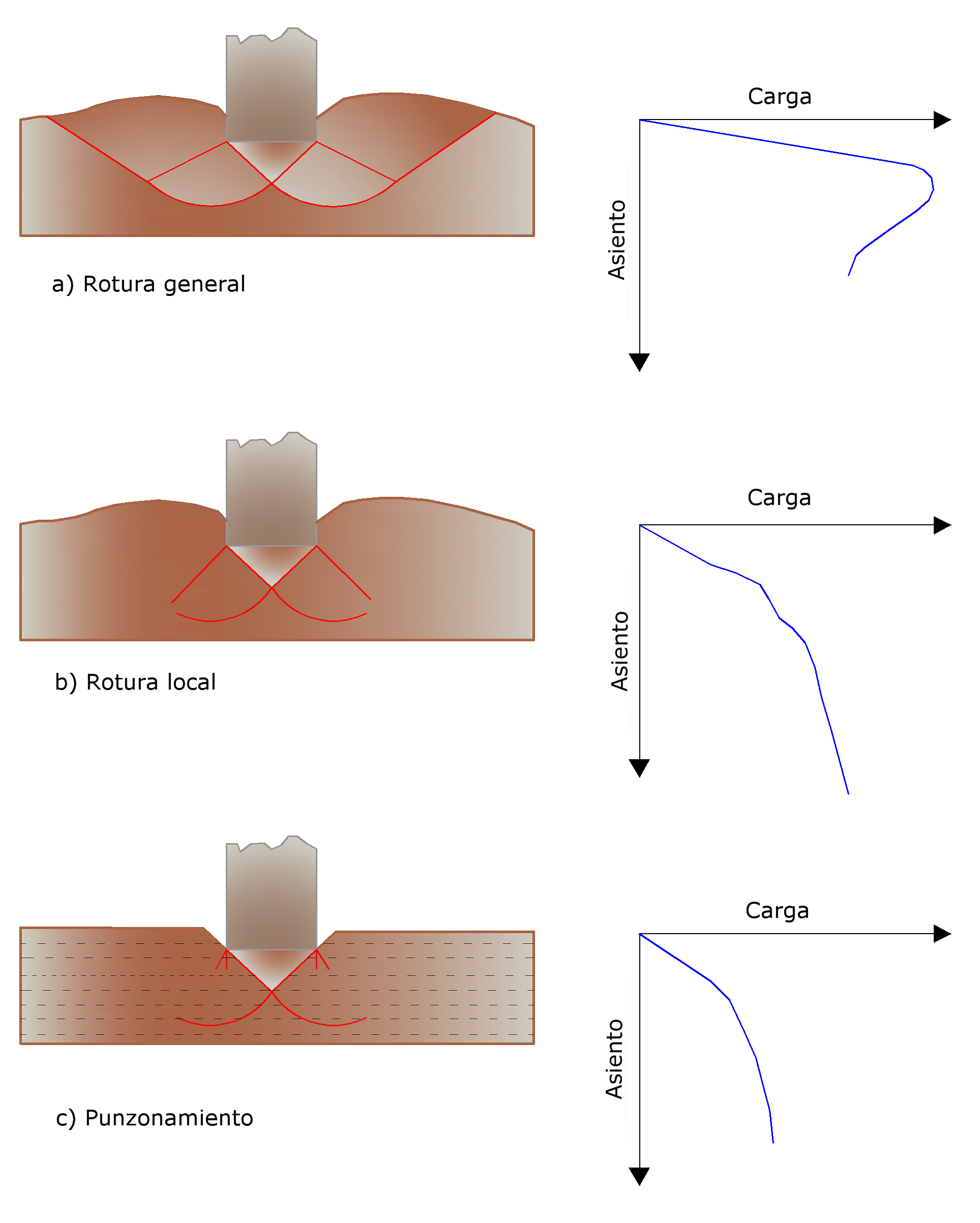
Figura 4.5.1- Tipos de rotura del terreno

 

 

Las soluciones disponibles para el cálculo de la carga última se basan en el supuesto de un comportamiento rígido-plástico del suelo y rigurosamente, por lo tanto, se pueden aplicar solo al caso de rotura general.

Se puede demostrar que la carga última de un terreno es la suma de tres factores: peso del terreno γ', sobrecarga q' y cohesión c'. Las soluciones con las que actualmente se cuenta se obtienen de la superposición de problemas individuales independientes.

 

Prandtl (1921) ha estudiado el problema de la rotura de un semiespacio elástico por efecto de una carga aplicada en su superficie con referencia al acero, caracterizando la resistencia a la rotura con una ley del tipo:

 

válida también para suelos.

 

Las hipótesis y las condiciones dictadas por Prandtl son las siguientes:

 

•Comportamiento rígido - plástico

•Resistencia a la rotura del material expresada con la relación (1-1)

•Carga uniforme, vertical y aplicada en una franja de longitud infinita y de ancho 2b (estado de deformación plana)

•Tensiones tangenciales iguales a cero al contacto entre la franja de carga y la superficie límite del semiespacio.

•Ausencia de sobrecarga en los bordes de la cimentación (q'=0)

 

En el acto de la rotura se verifica la plasticidad del material contenido entre la superficie límite del semiespacio y la superficie GFBCD. (véase Fig. 4.5.2)

En el triángulo AEB la rotura  se da según dos familias de segmentos rectilíneos e inclinados en 45°+φ/2 con respecto al horizontal.

 

En las zonas ABF y EBC la rotura se produce a lo largo de dos familias de líneas, una constituida por segmentos rectilíneos que pasan respectivamente por los puntos A y E  y la otra por arcos de familias de espirales logarítmicas. Los polos de éstas son los puntos A y E. En los triángulos AFG y ECD la rotura se da en segmentos inclinados en (45°+ φ/2) con respecto a la vertical.

 

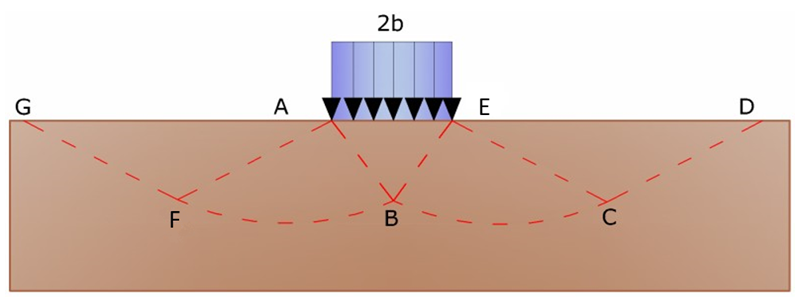
Figura 4.5.2- Solución de Prandl

 

Identificado el volumen de terreno que experimenta rotura con la carga última, esta se puede calcular escribiendo la condición de equilibrio entre fuerzas agentes en cualquier volumen de terreno delimitado bajo cualquiera de las superficies de deslizamiento. Se llega a la solución exacta que se exprime por medio de la ecuación:

 

donde el coeficiente B depende solo del ángulo de rozamiento φ' del terreno. Para φ'≠0 el factor B= 5,14.

En el caso particular de terreno sin cohesión (c'=0, γ'≠0) resulta q'=0. Según la teoría de Prandtl, no sería entonces posible aplicar ninguna carga en la superficie límite de un terreno incoherente.

 

Si bien no se puede aplicar prácticamente, en esta teoría se han basado todas las investigaciones y los métodos de cálculo sucesivos.

 

En efecto Caquot se puso en las mismas condiciones de Prandtl, a excepción del hecho que la franja de carga no se aplica sobre la superficie límite del semiespacio, sino a una profundidad h, con h ≤ 2b; el terreno comprendido entre la superficie y la profundidad h tiene las siguientes características: γ'=0, φ'≠0, c'=0 es decir un medio dotado de peso pero sin resistencia.  Resolviendo las ecuaciones de equilibrio se llega a la expresión:

 

 

que de seguro es un paso adelante con respecto a Prandtl, pero que aún no refleja la realidad.

 

 

Terzaghi (1955)

 
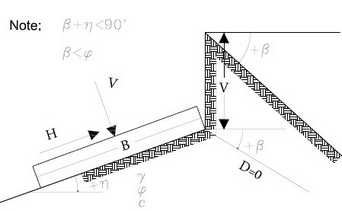
Terzaghi, prosiguiendo el estudio de Caquot, ha aportado algunos cambios para tener en cuenta las características del conjunto obra de cimentación - terreno.

Bajo la acción de la carga transmitida por la cimentación, el terreno que está en contacto con esta última tiende a retirarse lateralmente, pero se lo impiden las resistencias tangenciales que se producen entre la cimentación y el terreno; lo que implica un cambio del estado tensional en el terreno que se encuentra directamente bajo la cimentación. Para tenerlo en cuenta, Terzaghi asigna a los lados AB y EB de la cuña de Prandtl una inclinación Y respecto a la horizontal, seleccionando el valor de Y en función de las características mecánicas del terreno al contacto terreno-cimentación.

De esta manera se supera la hipótesis γ' =0 para el terreno bajo la cimentación admitiendo que las superficies de rotura quedan inalteradas, la expresión de la carga última entonces es:

 

 

donde:

 

C es un coeficiente que resulta función del ángulo de rozamiento interno φ del terreno bajo el nivel de cimentación y del ángulo j antes definido;

b es la semianchura de la franja.

 

Además, basándose en datos experimentales, Terzaghi pasa del problema plano al problema espacial introduciendo algunos factores de forma.

Terzaghi aportó otra contribución sobre el comportamiento efectivo del terreno.  En el método de Prandtl se supone un comportamiento del suelo rígido-plástico, mientras que Terzaghi supone este comportamiento en suelos muy compactos.  En estos, de hecho, la curva cargas-asientos presenta un primer tramo rectilíneo, seguido por un breve tramo curvilíneo (comportamiento elastoplástico); la rotura es instantánea y el valor de la carga límite se determina claramente (rotura general).

En un terreno muy suelto en cambio, la razón cargas-asientos presenta un tramo curvilíneo acentuado ya desde las cargas más bajas por efecto de una rotura progresiva del terreno (rotura local). Como consecuencia la identificación de la carga última no es tan clara y evidente como en el caso de los terrenos compactos.

Para los terrenos muy sueltos, Terzaghi aconseja, al calcular la carga última, tener en consideración el valor calculado con la fórmula anterior pero introduciendo valores reducidos de las características mecánicas del terreno, precisamente:

 

 

Haciendo explícitos los coeficientes de la fórmula anterior, la fórmula de Terzaghi se puede escribir así:

 

donde:

 

 

 

 

 

 

 

Meyerhof (1963)

 
Meyerhof propuso una fórmula para calcular la carga última parecida a la de Terzaghi. Las diferencias consisten en la introducción de nuevos coeficientes de forma.

Introdujo un coeficiente sq'  multiplica el factor Nq, factores de profundidad di y ii pendencia, para el caso en que la carga trasmitida a la cimentación sea inclinada en la vertical.

Los valores de los coeficientes N se obtuvieron de Meyerhof suponiendo varios arcos de prueba BF (v. mecanismo Prandtl), mientras que el corte a lo largo de los planos AF tenía valores aproximados. Los factores de N se presentan en la Tabla 4.5.1.

 

 

 

 

 

Tabla 4.5.1-Factores de forma, profundidad e inclinación de la fórmula de Meyerhof

 

 

 

Hansen (1970)

Es una extensión ulterior de la fórmula de Meyerhof; las extensiones consisten en la introducción de bi que considera la eventual inclinación en la horizontal del nivel de cimentación y un factor gi para terreno en pendencia. La fórmula de Hansen vale para cualquier razón D/B, ya sean cimentaciones superficiales o profundas; sin embargo el mismo autor introdujo algunos coeficientes para poder interpretar mejor el comportamiento real de la cimentación (véase tabla 4.5.2); sin estos, de hecho, se tendría un aumento demasiado fuerte de la carga última con la profundidad.

 

 

 

Tabla 4.5.2-Factores propuestos por Hansen para el cálculo de qlim

 

 

 

 

 

 

 

Vesic (1975)
La fórmula de Vesic es análoga a la fórmula de Hansen, con Nq y Nc como en la fórmula de Meyerhof y Nγ como se indica a continuación:

 

 

Los factores de forma y de profundidad que aparecen en las fórmulas del cálculo de la capacidad portante son iguales a los propuestos por Hansen; mientras se dan algunas diferencias en los factores de inclinación de la carga, del terreno (cimentación en talud) y del plano de cimentación (base inclinada).  

 

 

 

Brinch-Hansen (EC 7 - EC 8)

Para que una cimentación pueda resistir la carga de proyecto en seguridad con respecto a la rotura general, para todas las combinaciones de carga relativas al ELU (Estado límite último), se debe dar la siguiente desigualdad:

 

donde:

 

• Vd es la carga de proyecto al ELU, normal en la base de la cimentación, que incluye también el peso de la cimentación misma;

• Rd es la carga última de proyecto de la cimentación con respecto a las cargas normales, teniendo en cuenta también el efecto de cargas inclinadas o excéntricas.

 

En la evaluación analítica de la carga última de proyecto Rd se deben considerar las situaciones a corto y a largo plazo en los terrenos de grano fino.

 

La carga última de proyecto en condiciones no drenadas se calcula como:

 

donde:

 

 

 

En condiciones drenadas la carga última de proyecto se calcula como sigue:

 

donde:

 

 

 

 

Tabla 4.5.3- Factores correctivos propuestos por Brinch-Hansen en el cálculo de qlim

 

 

Además de los factores correctivos de la tabla anterior, se consideran los complementarios de la profundidad del plano de cimentación y de la inclinación y de la inclinación del plano de cimentación y del plano terreno (Hansen).

 

 

Meyerhof e Hanna (1973)

 

All the theoretical analysis dealt with so far is based on the assumption that the subsoil is isotropic and homogeneous to a considerable depth. In nature, soil is generally non-homogeneous with mixtures of sand, silt and clay in different proportions. In the analysis, an average profile of such soils is normally considered. However, if soils are found in distinct layers of different compositions and strength characteristics, the assumption of homogeneity to such soils is not strictly valid if the failure surface cuts across boundaries of such layers.

 

The present analysis is limited to a system of two distinct soil layers. For a footing located in the upper layer at a depth D, below the ground level, the failure surfaces at ultimate load may either lie completely in the upper layer or may cross the boundary of the two layers. Further, we may come across the upper layer strong and the lower layer weak or vice versa . In either case, a general analysis for (c = 0) will be presented and will show the same analysis holds true if the soil layers are any one of the categories belonging to sand or clay.

 

The bearing capacity of a layered system was first analyzed by Button (1953) who considered only saturated clay (φ = 0). Later on Brown and Meyerhof (1969) showed that the analysis of Button leads to unsafe results. Vesic (1975) analyzed the test results of Brown and Meyerhof and others and gave his own solution to the problem.

 

Vesic considered both the types of soil in each layer, that is clay and (c = 0) soils. However, confirmations of the validity of the analysis of Vesic and others are not available. Meyerhof (1974) analyzed the two layer system consisting of dense sand on soft clay and loose sand on stiff clay and supported his analysis with some model tests.

Again Meyerhof and Hanna (1978) advanced the earlier analysis of Meyerhof (1974) to encompass (c = 0) soil and supported their analysis with model tests. The present section deals briefly with the analyses of Meyerhof (1974) and Meyerhof and Hanna (1978).

 

 

Case 1: A Stronger Layer Overlying a Weaker Deposit

 

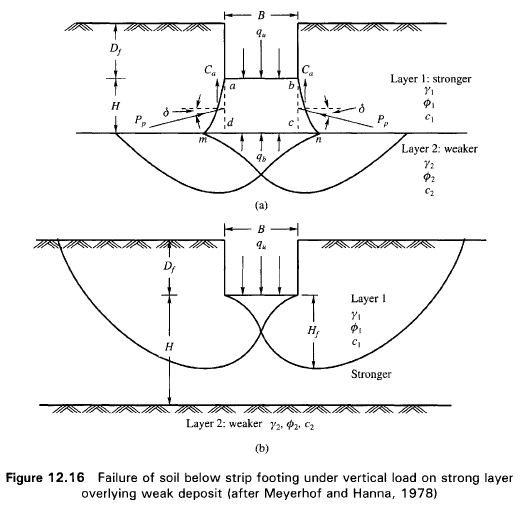
Figure 12.16(a) shows a strip footing of width B resting at a depth D, below ground surface in a strong soil layer (Layer 1). The depth to the boundary of the weak layer (Layer 2) below the base of the footing is H. If this depth H is insufficient to form a full failure plastic zone in Layer 1 under the ultimate load conditions, a part of this ultimate load will be transferred to the boundary level mn. This load will induce a failure condition in the weaker layer (Layer 2). However, if the depth H is relatively large then the failure surface will be completely located in Layer 1 as shown in Fig. 12.16b.
The ultimate bearing capacities of strip footings on the surfaces of homogeneous thick beds of Layer 1 and Layer 2 may be expressed as

 

 

If q1 is much greater that q2 and if the depth H is insufficient to form a full failure plastic condition in Layer 1, then the failure of the footing may be considered due to pushing of soil within the boundary ad and be through the top layer into the weak layer. The resisting force for punching may be assumed to develop on the faces ad and be passing through the edges of the footing. The forces that act on these surfaces are (per unit length of footing),

 

 

 

 

 

Richards et al.

 
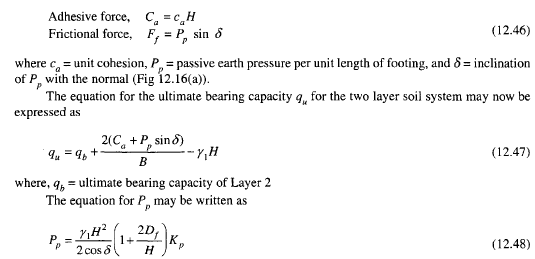
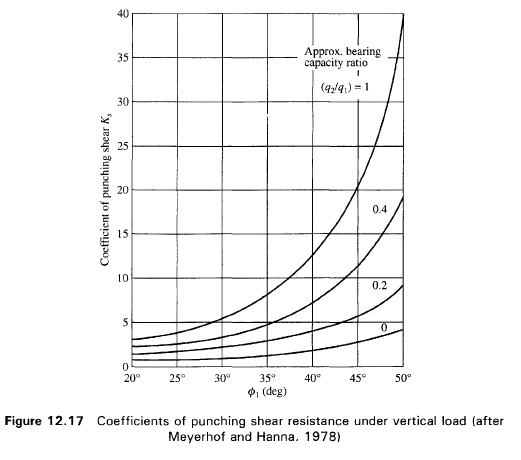
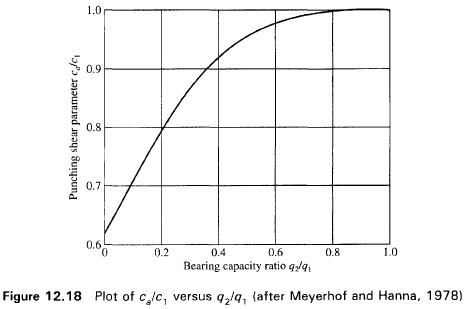
Richards, Helm y Budhu (1993) desarrollaron un procedimiento que permite, en condiciones sísmicas, calcular ya sea la carga última que los asientos derivados y por ende verificar ambos estados límite (último y de daño). El cálculo de la carga última se obtiene mediante una simple extensión del problema de la carga última al caso de la presencia de fuerzas de inercia en el terreno de cimentación debidas al sismo, mientras la estimación de los asientos se obtiene haciendo referencia a Newmark (Apéndice H de “Aspetti geotecnici della progettazione in zona sismica”–Associazione Geotecnica Italiana/"Aspectos geotécnicos del proyecto en zona sísmica"-Asociación Geotécnica Italiana). Los autores han alargado el trinomio de la fórmula de la carga última:

 

 

Donde los factores de capacidad de carga se calculan con las siguientes fórmulas:

 

 

Examinando con el enfoque de equilibrio límite un mecanismo a la Coulomb y teniendo en cuenta las fuerzas de inercia agentes en el volumen de terreno a rotura. De hecho, en campo estático, el clásico mecanismo de Prandtl se puede aproximar, como se muestra en la figura 4.5.3, eliminando la zona de transición (abanico de Prandtl) y reduciéndola a la línea AC, que viene vista como una pared ideal en equilibrio bajo la acción del empuje activo y del empuje pasivo que recibe de las cuñas I y III:

 

 

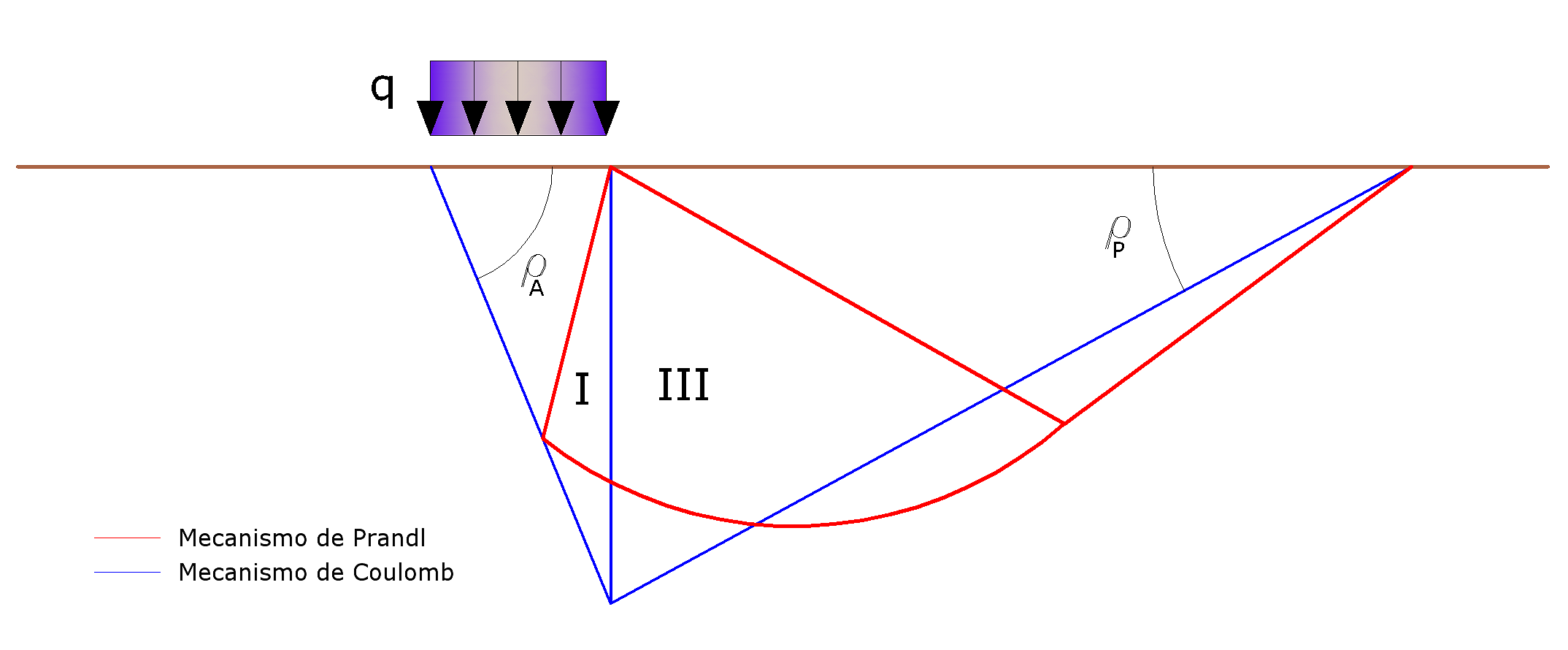
Figura 4.5.3- Esquema de cálculo de la carga última (qlim)

 

 

Los autores han extraído las expresiones de los ángulos ρA y ρP que definen las zonas de empuje activo y pasivo y de los coeficientes de empuje activo y pasivo KA y KP en función del ángulo de rozamiento interno φ del terreno y del ángulo de rozamiento d terreno – pared ideal:

 

 

 

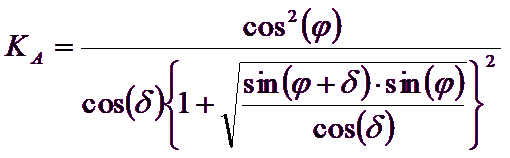
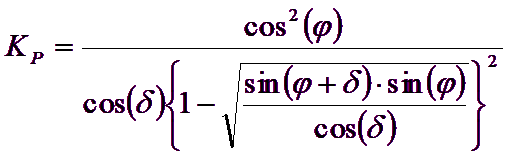
Es de observar que el empleo de las fórmulas anteriores asumiendo φ=0.5δ, conduce a valores de coeficientes de carga última muy cercanos a los basados en un análisis a la Prandtl. Por lo tanto Richards et. Al. extendieron la aplicación del mecanismo de Coulomb al caso sísmico, teniendo en cuenta las fuerzas de inercia agentes en el volumen de terreno a rotura. Tales fuerzas de masa, debidas a aceleraciones kh g y kv g, agentes respectivamente en dirección horizontal y vertical, son a su vez iguales a kh g y kv g. Se obtienen así las extensiones de las expresiones de ρA y ρP, además de KA y KP, respectivamente indicadas como ρAE y ρPE y como KAE y KPE para denotar las condiciones sísmicas:

 

 

 

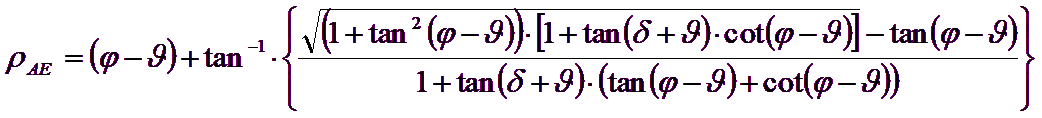
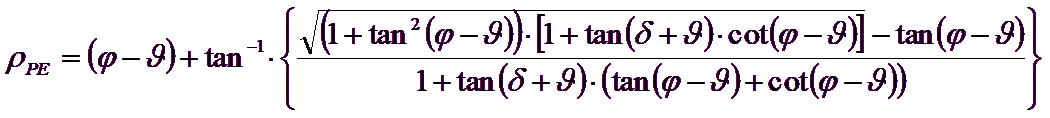
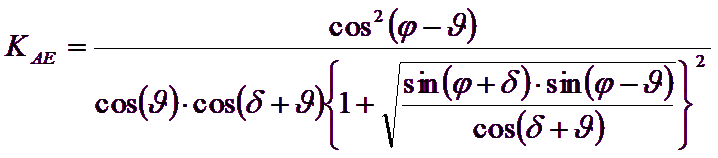
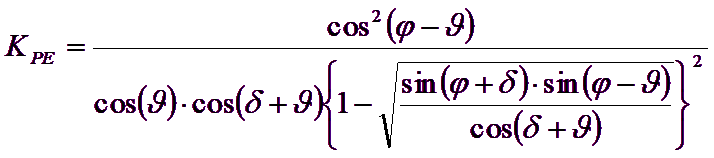
Los valores de Nq y Nγ se determinan también valiéndose de las fórmulas precedentes, empleando obviamente las expresiones de los ángulos ρAE y ρPE y de los coeficientes KAE y KPE relativas al caso sísmico. En tales expresiones aparece el ángulo q definido como:

 

 

En la Tabla 4.5.4 se muestran los factores de capacidad de carga calculados para los siguientes valores de los parámetros:

 

ϕ = 30°
δ = 15°

 

Y para diferentes valores de los coeficientes de empuje sísmico:

 

 

Tabla 4.5.4.- Factores de capacidad de carga para f=30°

 

 

Carga última de cimentación en roca

 

Para estimar la capacidad de carga admisible de las rocas se deben considerar algunos parámetros significativos como las características geológicas, el tipo y calidad de roca, medida con RQD. En la capacidad portante de las rocas se utilizan normalmente factores de seguridad muy altos y unidos en alguna manera al valor del coeficiente RQD: por ejemplo, para una roca con RQD igual al máximo de 0.75 el factor de seguridad varía entre 6 y 10. Para determinar la capacidad de carga de una roca se pueden usar las fórmulas de Terzaghi, usando ángulo de rozamiento y cohesión de la roca, o las propuestas por Stagg y Zienkiewicz (1968) donde los coeficientes de la fórmula de la capacidad portante valen:

 

 

 

Con tales coeficientes se usan los factores de forma utilizados en la fórmula de Terzaghi.

La capacidad de carga última calculada es siempre función del coeficiente RQD según la siguiente expresión:

 

 

Si el sondeo en roca no suministra piezas intactas (RQD tiende a 0), la roca se trata como un terreno, estimando mejor los parámetros c y φ.

 

 

Verificación del deslizamiento

De acuerdo con los criterios de cálculo en ELU, se debe comprobar la estabilidad de una zapata aislada con respecto al colapso por deslizamiento y al colapso por rotura general. Con el primero, la resistencia se estima como la suma de un componente debido a la adhesión más otro debido al rozamiento cimentación-terreno; la resistencia lateral derivada del empuje pasivo del terreno se puede tener en cuenta como un porcentaje cuyo valor será indicado por el usuario.

La resistencia de cálculo por rozamiento y adhesión se calcula mediante la expresión:

 

donde:

 

Nsd        valor de cálculo de la fuerza vertical;

δ                ángulo de resistencia al corte en la base de la cimentación;

ca                adhesión zapata -terreno;

A'                área de la cimentación efectiva, entendida, en caso de cargas excéntricas, como área reducida al centro de la cual se aplica el resultado.

 

 

 

Cálculo de los asientos

La aplicación de una carga de dimensiones finitas sobre un terreno cohesivo genera una serie de fenómenos, los cuales se pueden ilustrar como en la Fig. 4.5.4.

 

 

 

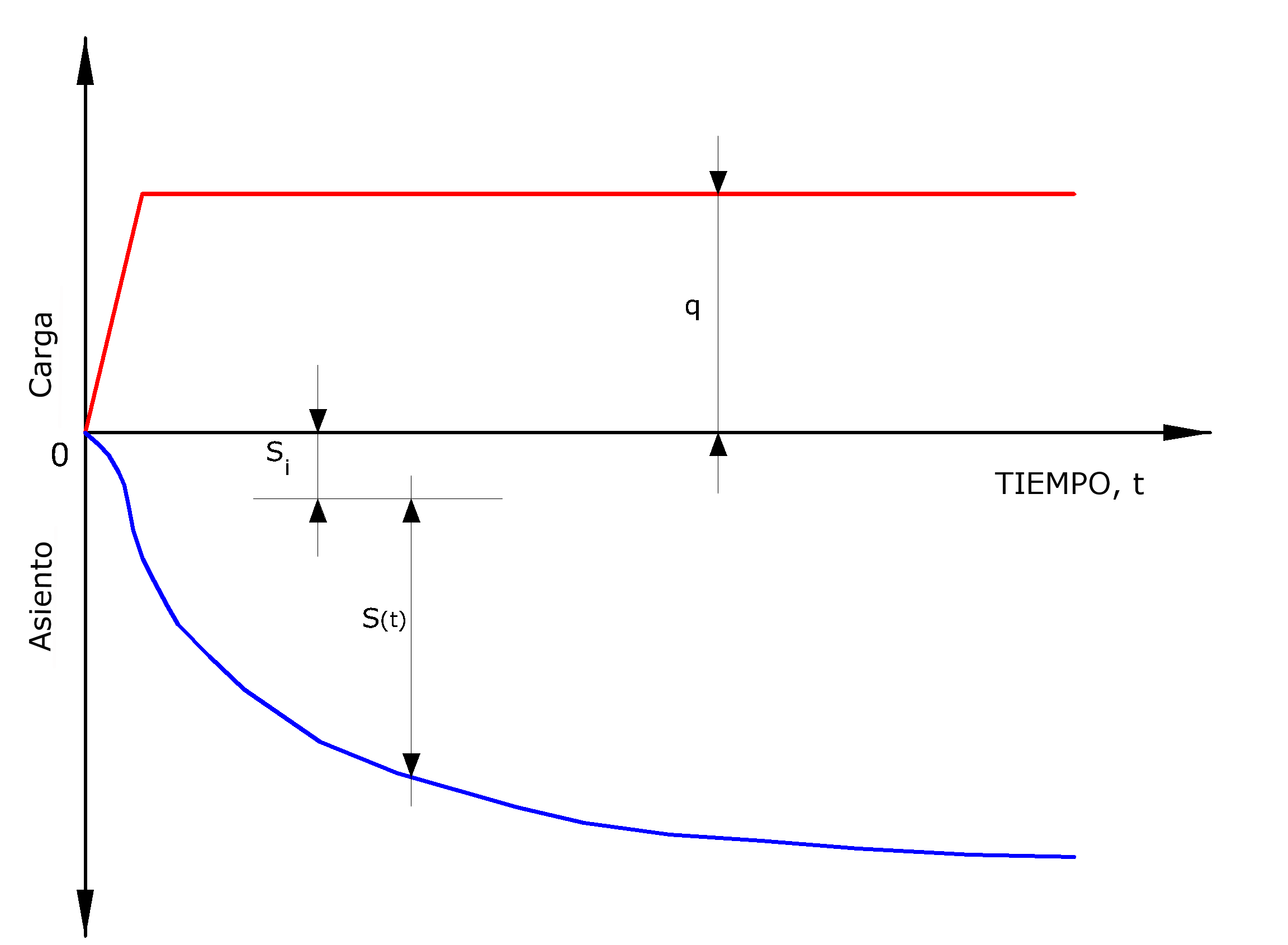
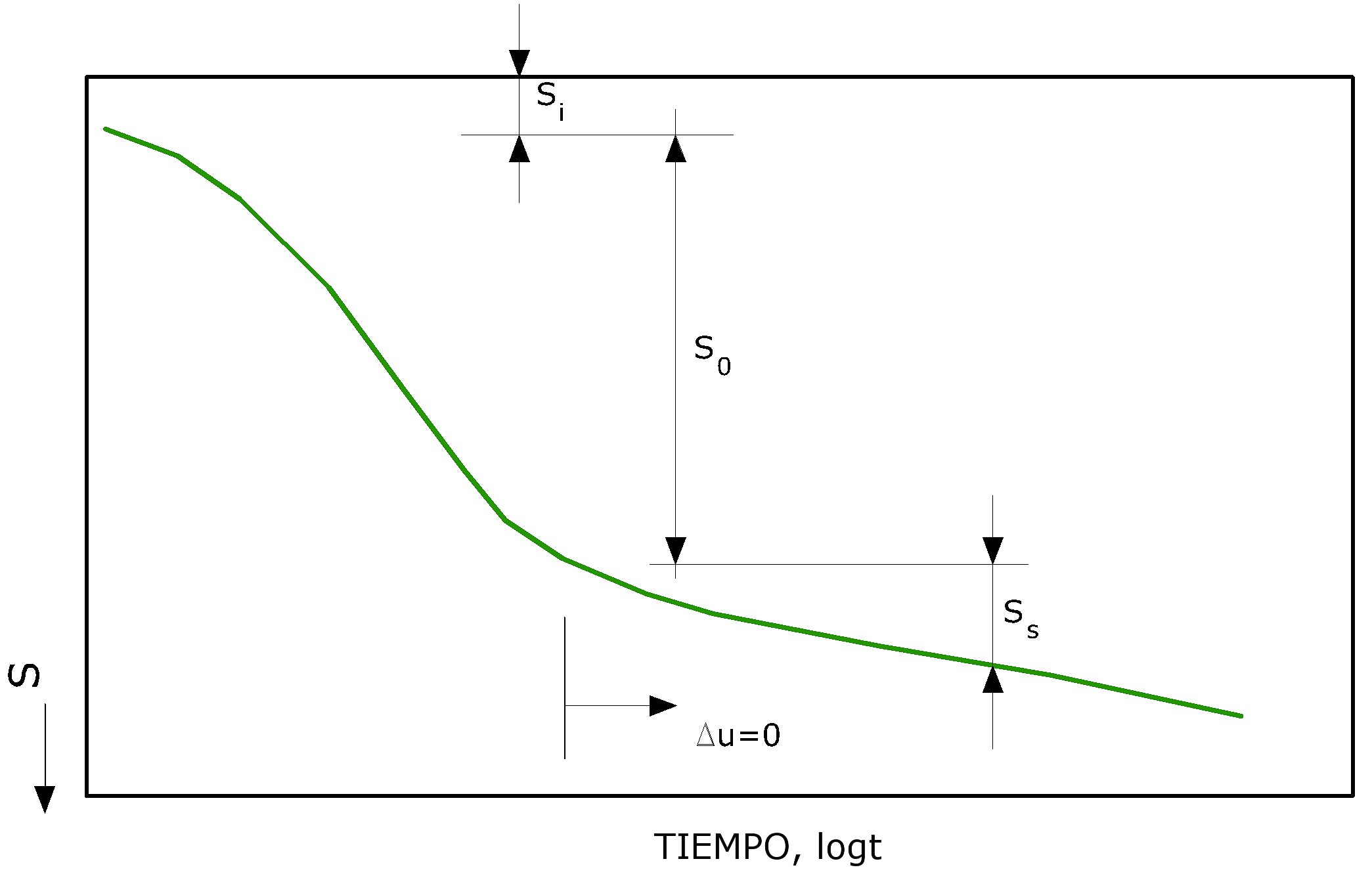
Figura 4.5.4.- Tipos de asientos

 

 

1.Durante la fase de carga, en el terreno se producen subpresiones del agua intersticial Δu, y dada la baja permeabilidad del terreno, se puede asumir que, en el ámbito de las usuales velocidades de aplicación de la carga, nos encontremos en condiciones no drenadas. El estrato de arcilla se deforma a volumen casi constante y el consiguiente asiento se indica como asiento inmediato.

2.La instauración del drenaje, con la transferencia progresiva de la carga de la base fluida a la armazón sólida, comporta ulteriores asientos cuya velocidad en el tiempo depende principalmente de las condiciones de drenaje. Este proceso se conoce como consolidación primaria y el análisis se lleva a cabo con los diferentes modelos de la teoría de la consolidación. El asiento que deriva de este proceso de expulsión del agua de los vacíos intersticiales se denomina asiento de consolidación.

3.Por último, aún cuando las sobrepresiones intersticiales se disipan (Δu=0), continúan a darse en el tiempo asientos debidos a deformaciones viscosas en condiciones drenadas y este asiento se conoce como asiento secundario.

 

El comportamiento de los terrenos de grano grueso (arenas y gravas) resulta macroscópicamente diferente a los de grano fino (limos y arcillas) debido a la diferente permeabilidad.

En este caso se habla de asiento inicial y secundario para indicar los asentamientos de naturaleza elasto-plástica y los debidos a fenómenos de naturaleza viscosa.

 

 

Asientos elásticos

Los asientos de una cimentación rectangular de dimensiones B'xL' ubicada en la superficie de un semiespacio elástico, se pueden calcular por medio de una ecuación basada en la teoría de la elasticidad (Timoshenko e Goodier (1951)):

 

 

(1)

 

 

donde:

 

q0         Intensidad de la presión de contacto;

B'         Mínima dimensión del área reactiva;

Es e ν  Parámetros elásticos del terreno;

Ii = f(L'/B', H, m, D)  Coeficientes de influencia dependientes de: L'/B', espesor del estrato H, Coeficiente de Poisson ν, profundidad del nivel de cimentación D;

IF  Coeficiente de influencia.

 

Los coeficientes I1 y  I2 se pueden calcular utilizando las ecuaciones de Steinbrenner (1934) (V. Bowles), en función de la razón M=L'/B' ed N=H/B, utilizando B'=B/2 e L'=L/2 para los coeficientes Ii  del centro y B'=B e L'=L para los coeficientes Ii del borde. El coeficiente de influencia IF deriva de las ecuaciones de Fox (1948), que indican que el asiento se reduce con la profundidad en función del coeficiente de Poisson y de la razón L/B. Para simplificar la ecuación (1) se introduce el coeficiente IS:

 

 

Se puede escribir la fórmula (1) en su versión más compacta:

 

 

Esta ecuación se puede aplicar a cimentaciones flexibles o rígidas con los oportunos cambios del valor de Is.

Analizando un cierto número de casos, el autor concluye que para que la ecuación anterior dé buenos resultados, se debe aplicar como sigue:

 

1.Efectuar la mejor estimación de q0;

2.Convertir la cimentación, si es circular, en una cimentación cuadrada equivalente.

3.Determinar el punto donde calcular el asiento y subdividir la base de apoyo en forma tal que el punto se encuentre en correspondencia de una arista interna común a varios rectángulos.

4.El espesor del estrato H responsable del asiento se toma como el mínimo de los dos siguientes valores: profundidad z=5B donde B es la dimensión mínima global de la base de la cimentación; profundidad a la cual se encuentra un estrato duro (ES del estrato debe ser aproximadamente 10 veces el valor del espesor adyacente).

5.Calcular correctamente la razón H/B'. Con un espesor del estrato H=z=5B se encuentra, para el centro de cimentación

   H/B'=5B/0,5B=10B, para una arista 5B/B=5.

6.Obtener Is con una estimación cuidadosa de m y tomando los  coeficientes de influencia I1 y I2 de la tabla que propone el autor.

7.Obtener IF con la ayuda de la Fig. 4.5.5.

8.Obtener Es en el espesor del estrato z=H como promedio ponderado de los valores de Esi de cada estrato en el espesor Hi.

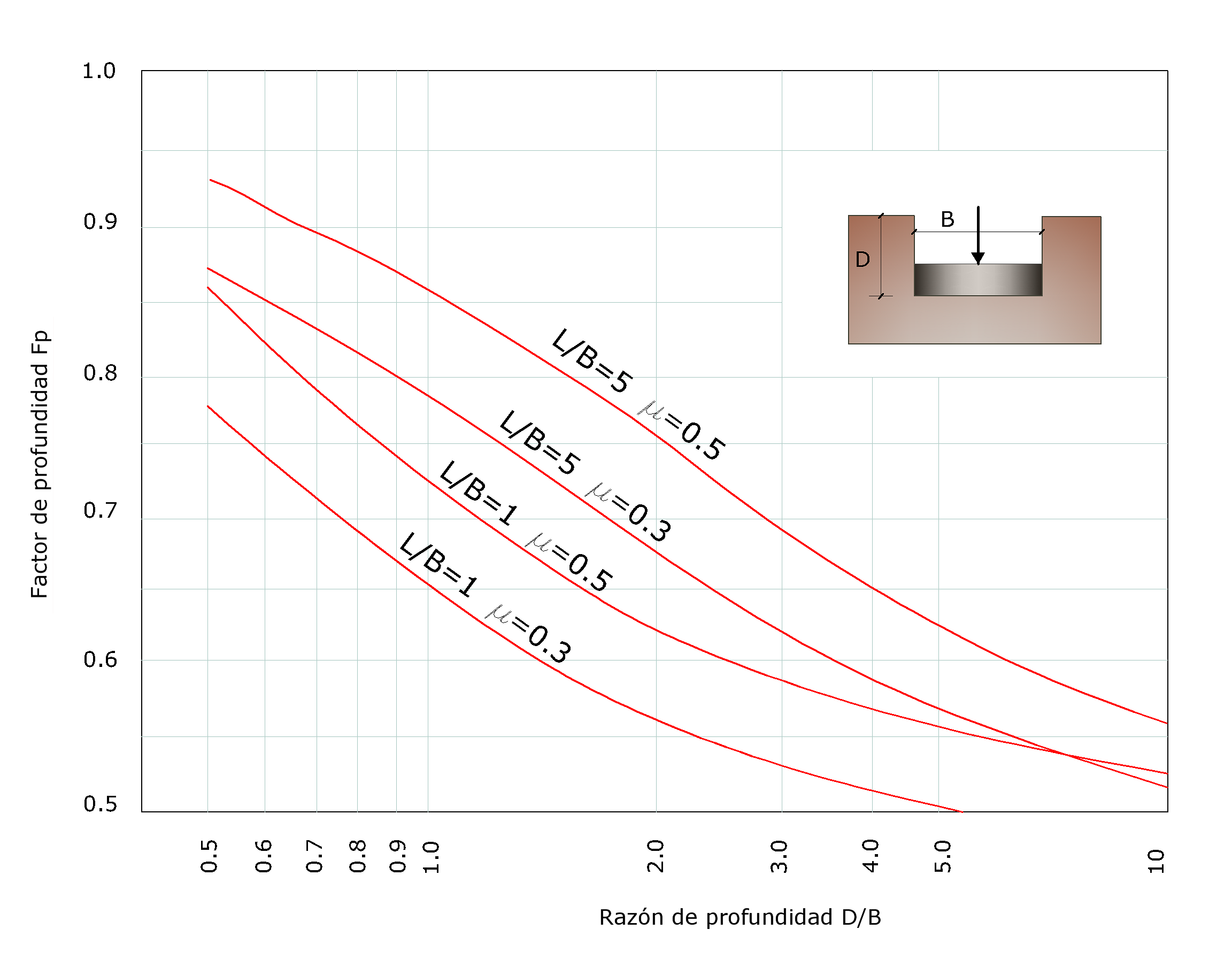
Fig. 4.5.5.-Coeficiente de influencia IF  de una cimentación colocada en profundidad D.

 

 

 

Asientos edométricos

El cálculo de los asientos con el método edométrico permite estimar un asiento de consolidación unidimensional (Terzaghi-1943), producto de las tensiones inducidas por una carga aplicada en condiciones de expansión lateral impedida. Por lo tanto la estimación con este método se debe considerar empírica, en vez de teórica.

No obstante esto, la simplicidad de uso y la facilidad de controlar la influencia de los varios parámetros que intervienen en el cálculo, lo convierten en un método muy utilizado.

Según el esquema de la Fig. 4.5.6., el asiento DH de un estrato con espesor inicial H0 está dado por:

 

 

 

 

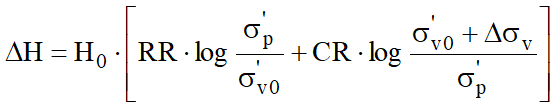
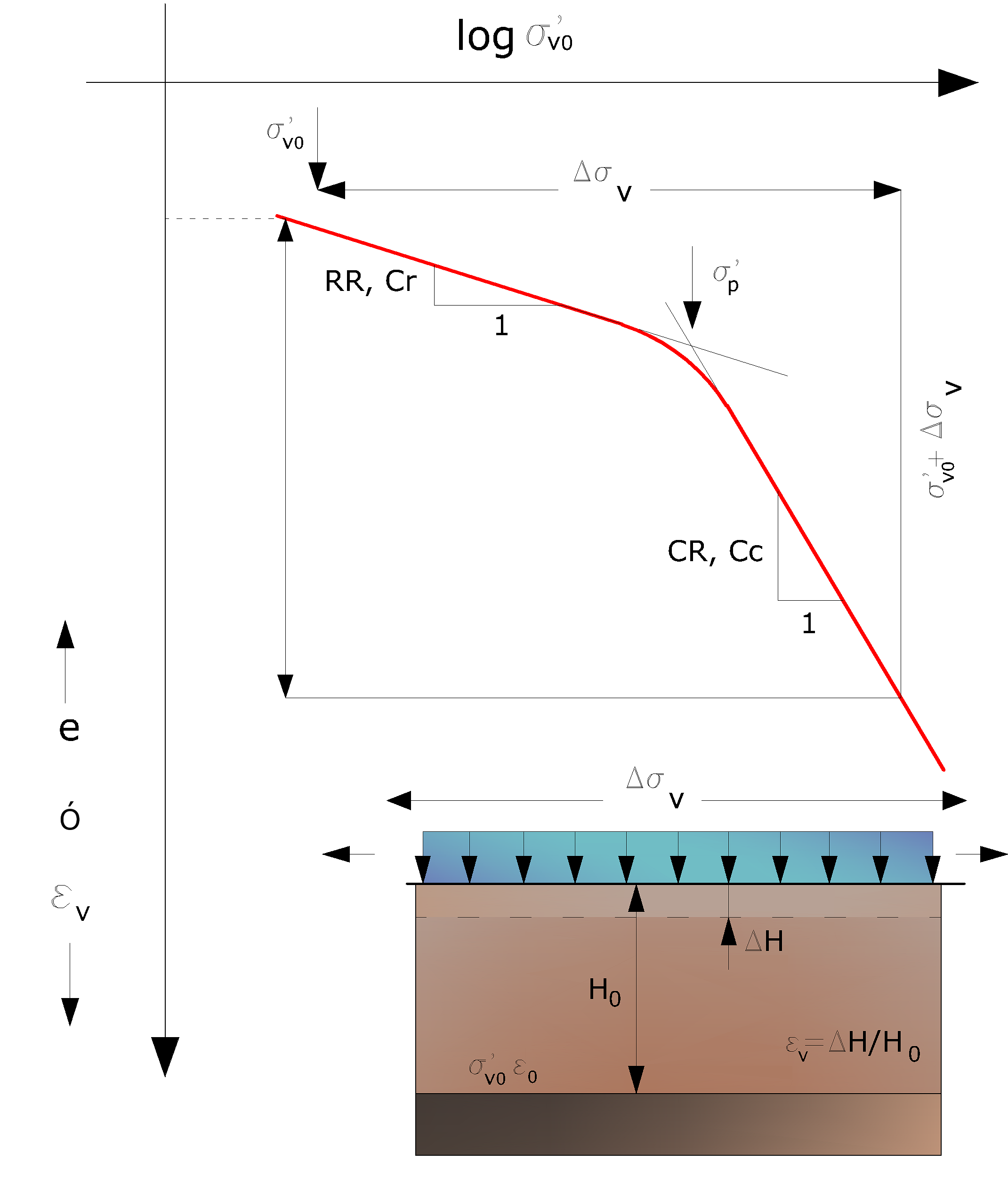
Figura 4.5.6.-Asiento edométrico

 

 

El enfoque edométrico en el cálculo de los asientos pasa esencialmente por dos fases:

 

1. El cálculo de las tensiones verticales inducidas en las diferentes profundidades con la aplicación de la teoría de la elasticidad (enfoque de Boussinesq, Westergaard...);

2. El cálculo de los parámetros de compresibilidad con la prueba edométrica.

En referencia a los resultados de la prueba edométrica, el asentamiento se estima de la siguiente manera:

 

 

si se trata de un terreno sobreconsolidado (OCR>1), o sea si el incremento de tensión debido a la aplicación de la carga no hace que se supere la presión de preconsolidación σ’p (σ'v0 + Δσv < σ'p).

Si en cambio el terreno es normalmente consolidado (σ'v0=σ'p) las deformaciones se dan en el tracto de compresión y el asiento se calcula como:

 

donde:

 

RR        Razón de recompresión;

CR        Razón de compresión;

H0        espesor inicial del estrato;

σ'v0        tensión vertical eficaz antes de la aplicación de la carga;

Δσv        incremento de tensión vertical debido a la aplicación de la carga.

 

Como alternativa a los parámetros RR y CR se hace referencia al módulo edométrico M; pero en tal caso se debe seleccionar oportunamente el valor del módulo a utilizar, teniendo en cuenta el intervalo tensional ( σ'v0 + Δσv  ) significativo para el problema examinado. Una correcta aplicación de este enfoque requiere:

 

•la subdivisión de los estratos compresibles en una serie de pequeños estratos de modesto espesor  (< 2.00 m);

•la estimación del módulo edométrico en el ámbito de cada estrato;

•el cálculo del asiento como suma de las contribuciones para cada pequeño estrato.

 

Muchos usan las expresiones antes indicadas para el cálculo del asentamiento de consolidación tanto para las arcillas como para las arenas de granulometría de fina a media, porque el módulo de elasticidad usado viene tomado directamente de pruebas de consolidación. Sin embargo, para terrenos con grano más grueso las dimensiones de las pruebas edométricas no son muy indicativas del comportamiento global del estrato y, para las arenas, es preferible utilizar pruebas penetrométricas estáticas y dinámicas.

 

 

Asiento secundario

El asiento secundario se calcula según la razón:

 

 

donde:

 

Hc        es la altura del estrato en fase de consolidación;

Cα        es el coeficiente de consolidación secundaria como pendencia en el tracto secundario de la curva asiento-logaritmo tiempo;

T        tiempo en que se desea calcular el asiento secundario;

T100        tiempo necesario para terminar el proceso de consolidación primaria.

 

Los supuestos de este método son:

 

•la consolidación secundaria inicia después de terminado el proceso de consolidación primaria;

•el valor de Ca se puede considerar constante mientras se da el asiento secundario.

 

 

Método de Schmertmann

Un método alternativo para calcular los asientos es el propuesto por Schmertmann (1970), el cual ha correlaciona la variación del bulbo tensiones a la deformación. Schmertmann por lo tanto propone considerar un diagrama de las deformaciones de forma triangular (Fig. 4.5.7) donde la profundidad a la cual se tienen deformaciones significativas se toma como igual a 4B, en el caso de cimentaciones corridas, para cimentaciones cuadradas o circulares es igual a 2B.

 

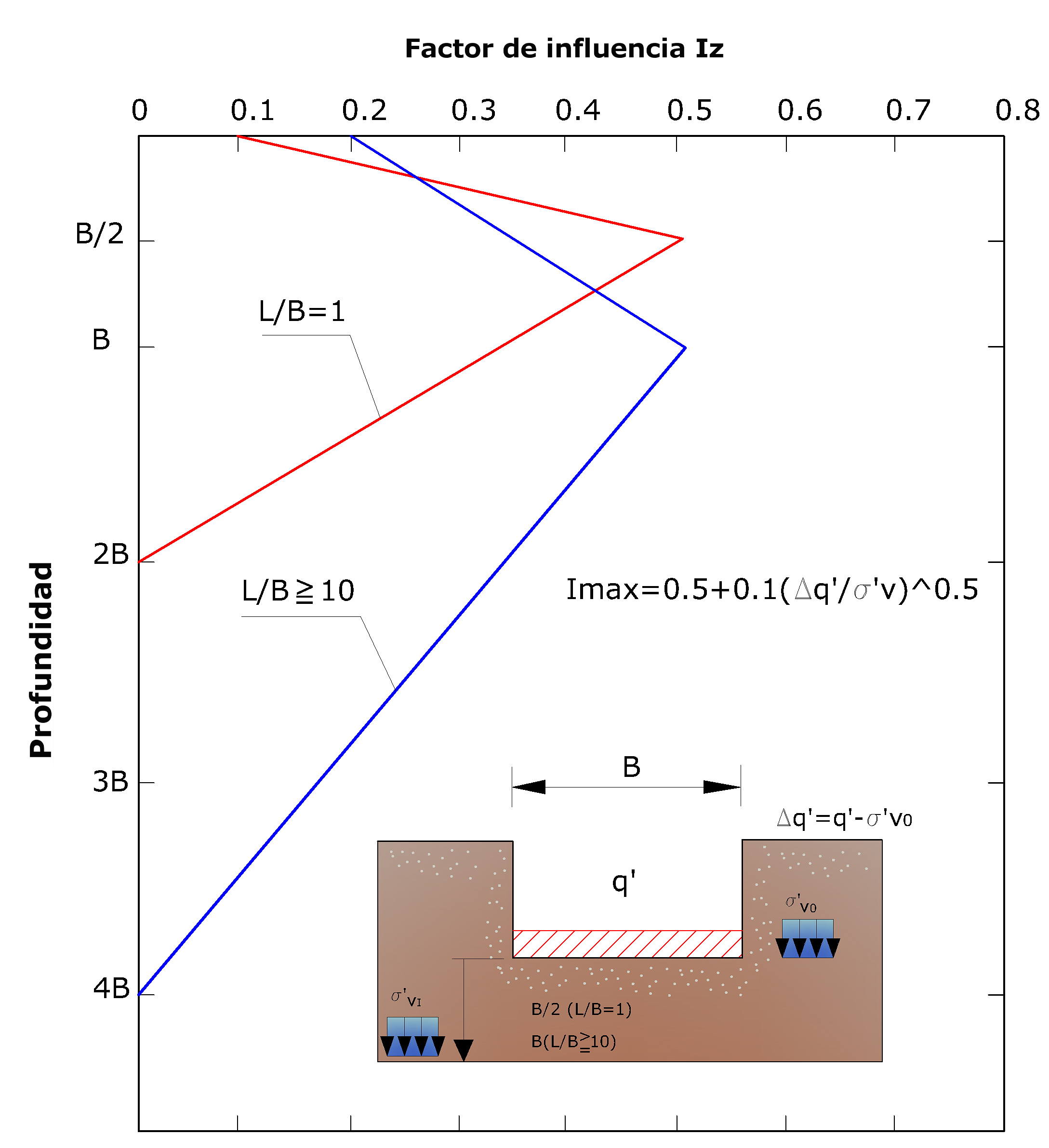
Fig. 4.5.7.- Variación del factor de influencia según la profundidad

 

 

Según este enfoque el asiento se expresa mediante la siguiente ecuación:

 

 

donde:

 

Δq                representa la carga neta aplicada a la cimentación;

Iz        es un factor de deformación cuyo valor es nulo a la profundidad de 2B, para cimentaciones circulares o cuadradas, y a profundidad 4B, para cimentaciones corridas.

 

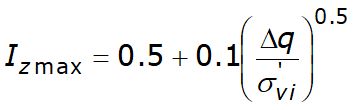
donde:

 

σ'v0        representa la tensión vertical eficaz a la profundidad B/2 para cimentaciones circulares o cuadradas, y a profundidad B para cimentaciones corridas

Ei        representa el módulo de deformación del terreno correspondiente al estrato i-ésimo considerado en el cálculo;

Δzi        representa el espesor del i-ésimo estrato;

C1 y C2 son dos coeficientes correctivos.

 

El módulo Ei se considera igual a 2.5 qc para cimentaciones circulares o cuadradas e igual a 3.5 qc para cimentaciones corridas. En los casos intermedios, se interpola en función del valor de L/B.

El término qc que interviene en la determinación de E representa la resistencia a la puntaza obtenida con la prueba CPT.

Las expresiones de los dos coeficientes C1 y C2 son:

 

 

 

 

En la expresión anterior, t representa el tiempo, expresado en años después de haber terminado la construcción, de acuerdo con el cual se calcula el asentamiento.

 

 

 

Burland y Burbidge

 

Si para calcular los asentamientos se dispone de datos obtenidos con ensayos penetrométricos dinámicos, entonces es posible valerse del método de Burland y Burbidge (1985), en el cual se relaciona un índice de compresibilidad Ic al resultado NSPT del ensayo penetrométrico dinámico. La expresión del asiento propuesta por los autores es la siguiente:

Donde:

 

q'                es la presión eficaz bruta;

σ'v0                es la tensión vertical eficaz en la cota establecida de la cimentación;

B                es el ancho de la cimentación;

Ic                es el índice de compresibilidad;

fS, fH, ft        son factores correctores que consideran respectivamente la forma, el espesor del estrato comprensible y el componente viscoso de los asientos.

 

El índice de compresibilidad Ic está legado al valor medio NAV de Nspt al interno de una profundidad significativa zi (que el software calcula en automático):

 

 

 

Con respecto a los valores de Nspt a utilizar en el cálculo del valor medio NAV, hay que precisar que los valores se deben corregir para arenas con componentes limosos bajo el nivel freático y Nspt>15, según la indicación de Terzaghi y Peck (1948)

 

 

donde Nc es el valor correcto a usar en los cálculos.

Para depósitos gravosos arenosos-gravosos el valor corregido es igual a:

 

 

 

Las expresiones de los factores correctores fS, fH y ft son respectivamente:

 

 

con:

t = tiempo en años > 3;

R3 = constante igual a 0.3 para cargas estáticas ye 0.7 para cargas dinámicas;

R = 0.2 en el caso de cargas estáticas y 0.8 para cargas dinámicas.

 

 

 

Verificación de la licuefacción

 

El fenómeno de la licuefacción tiene que ver con los depósitos arenosos saturados que, durante un evento sísmico o más ampliamente durante e inmediatamente después de una solicitación cíclica, sufren una drástica reducción de la resistencia al corte.

Es generalmente aceptado que la causa principal de la licuefacción de los terrenos arenosos saturados, que se produce durante los eventos sísmicos, sea debida al aumento de las presiones intersticiales originadas por las solicitaciones de corte cíclicas, que a su vez han de atribuirse a la propagación de las ondas de corte en el terreno. La aplicación de una sucesión de esfuerzos cíclicos en condiciones drenadas genera inicialmente una reducción de volumen; sin embargo, si la solicitación se da muy rápidamente con respecto a la capacidad de drenaje del depósito, sucede que la reducción de volumen no puede manifestarse y el mismo será sometido a un proceso de carga no drenada.El impedimento de la deformación volumétrica se acompaña de un aumento de la presión de poro y de una reducción de las tensiones efectivas, con las tensiones totales constantes. El aumento de presión neutra depende del grado de densificación inicial del terreno y del tipo de solicitación cíclica.

Si el terreno se encuentra en estado poco denso y la solicitación cíclica resulta suficientemente elevada, el incremento de presión neutra resultante puede igualar la tensión efectiva de confinamiento y las partículas de terreno ya no estarán sujetas a ningún esfuerzo intergranular.En tales condiciones y siendo la cohesión nula, el terreno ya no tiene ninguna resistencia al corte.

 

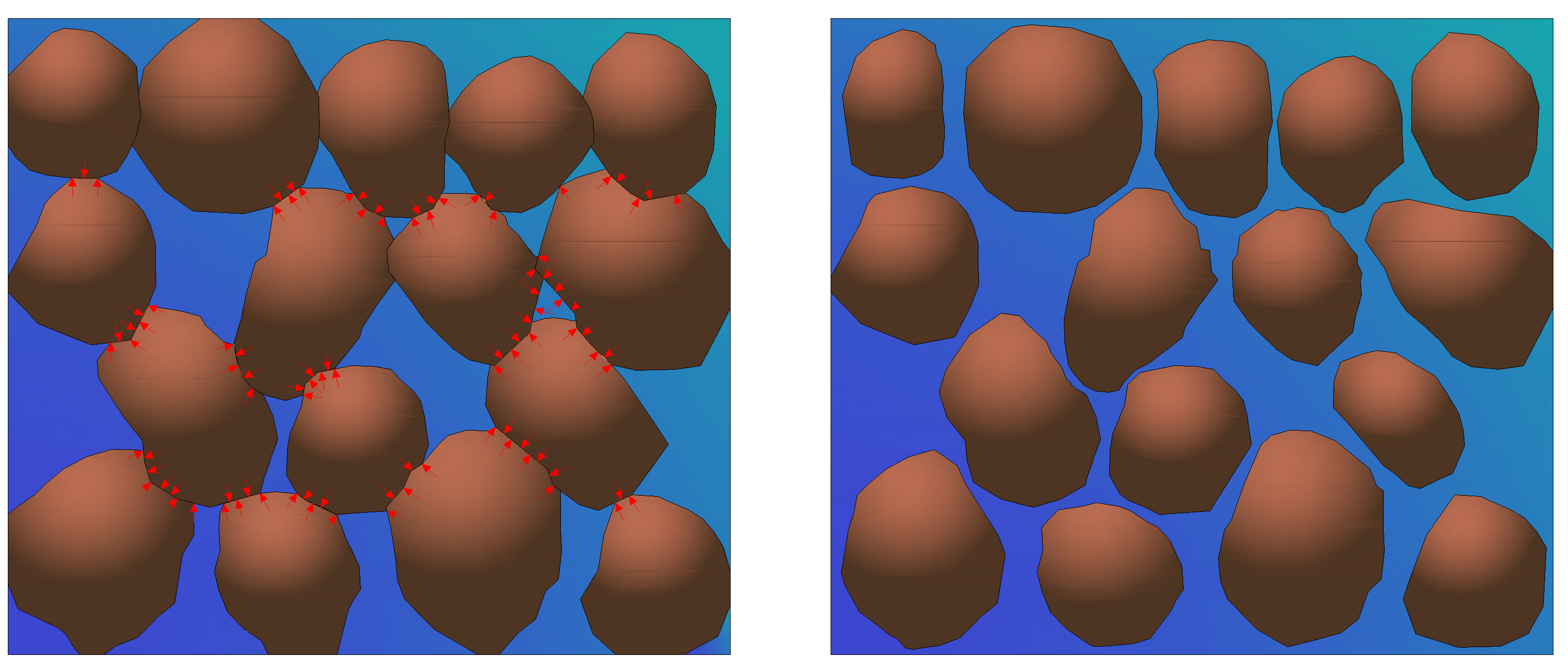
Suelo arenoso saturado antes del efecto de la licuefacción (izquierda), se notan las tensiones entre los granos representadas con las flechas rojas. Suelo arenoso saturado con proceso de licuefacción,  tensiones intergranulares ausentes.

 

 

CASOS EN LOS QUE SE PUEDE EXCLUIR LA PRESENCIA DE FENÓMENOS DE LICUEFACCIÓN (EC8)

La verificación de la licuefacción se podrá obviar cuando se manifieste por lo menos una de las siguientes circunstancias:

 

1.Eventos sísmicos esperados de magnitud M menor que 5;

2.Aceleración máxima esperada en superficie menor que 0.1 g;

3.Aceleración máxima esperada en superficie menor que 0.15 g y suelos con características pertenecientes a una de las tres siguientes categorías:

 FC>20%, IP>10;

 FC≥ 35%, N’SPT (corregido-normalizado) >20;

 FC≤5%,  N’SPT (corregido-normalizado) >25 ;

 

4. Material con Uc < 3.5 – Granulometría del suelo externa a las zonas indicadas en la Fig. 4.5.9;

   Material con Uc >3.5 – Granulometría del suelo externa a las zonas indicadas en la Fig. 4.510

5. Profundidad promedio estacional del nivel freático mayor a los 15 m (siempre que el plano del terreno sea sub-horizontal y estructuras con cimentaciones superficiales).

 

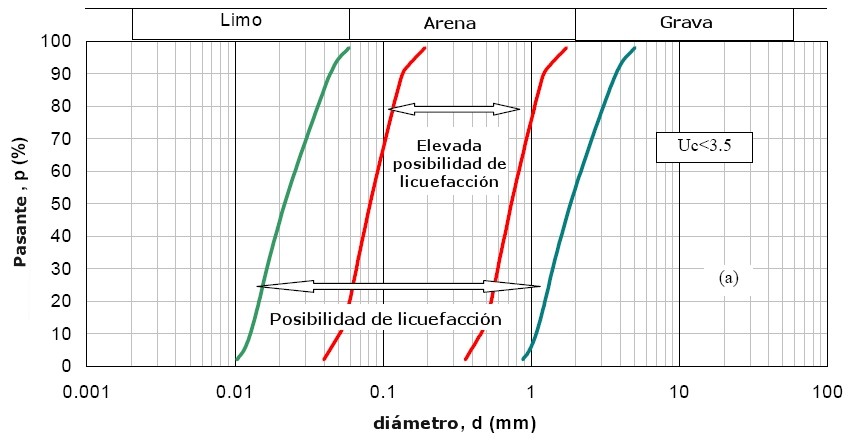
Figura 4.5.9 – Tramos granulométricos críticos Uc< 3.5

 

 

 

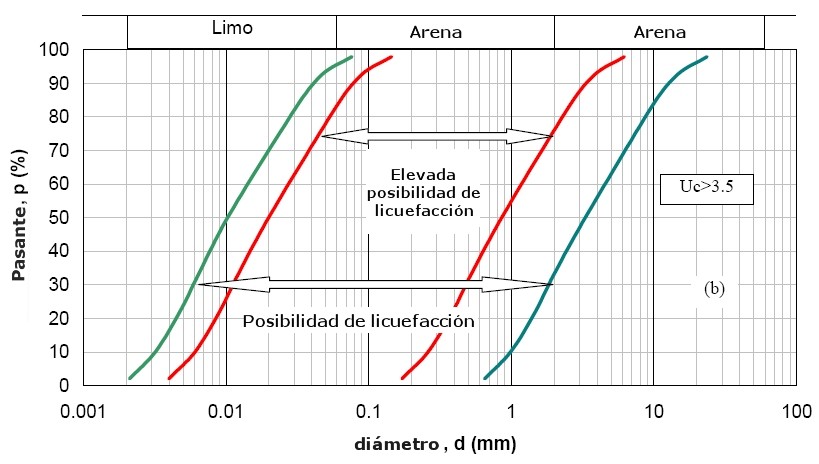
Figura 4.5.10 – Tramos granulométricos críticos Uc>3.5

 

 

Seed e Idriss

El método que utiliza LoadCap para determinar la licuefacción de un terreno arenoso durante un evento sísmico es el propuesto por Seed e Idriss, el cual es el más conocido y utilizado de los métodos simplificados.

Dicho método se basa en el número de golpes del ensayo Standard Penetration Test y requiere de pocos parámetros geotécnicos: la granulometría, la densidad relativa, el peso de volumen.

El factor de resistencia a la licuefacción FS se deriva de la relación entre la capacidad de resistencia normalizada (R) y el esfuerzo cíclico resistente (T), multiplicado por un factor de escala que se estima considerando un evento sísmico esperado de magnitud M=6.5 que asume un valor constante igual a 1.19 (peor condición).

La capacidad de resistencia normalizada con respecto a la tensión vertical efectiva inicial se expresa con:

 

y se puede determinar a partir del gráfico de la Fig. 4.5.11, función de parámetros obtenidos con ensayos  SPT oportunamente corregidos y normalizados.

 

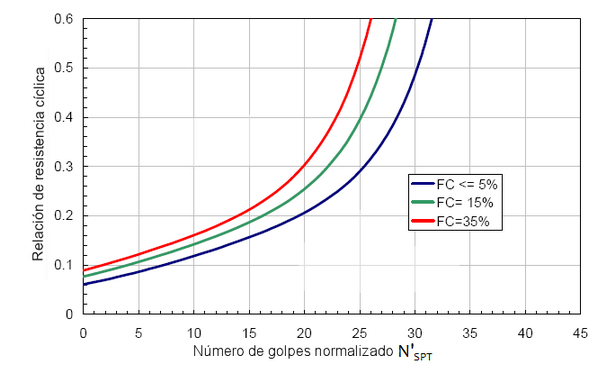
Figura 4.5.11 – Correlación entre capacidad de resistencia cíclica y número de golpes corregido del ensayo penetrométrico dinámico (N'SPT)

 

La relación de esfuerzos cíclicos se expresa como:

dove:

donde:

g                aceleración de la gravedad;

σv, σ'v        respectivamente, tensión vertical total y tensión vertical efectiva a la profundidad considerada;

rd = 1-0.015z        factor de reducción que tiene en cuenta la deformabilidad del terreno al pasar de las ondas sísmicas de corte.

En la expresión de esfuerzos cíclicos (T), para tener en cuenta el carácter esporádico de los picos de aceleración, se corrige el esfuerzo máximo cíclico inducido por el evento sísmico del 35% obteniendo un valor de "esfuerzo equivalente uniforme".

Si FS>1.3 el depósito se considera no licuable.

 

 

 

©  GeoStru