The vertical bearing capacity of the foundation soil is verified according to the theory of limit states using the following inequality:
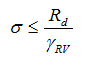
or based on the factor of safety as:
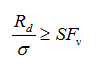
where:
σ extreme design contact stress at the footing bottom
Rd design bearing capacity of foundation soil
γRV coefficient of vertical bearing capacity of foundation
SFv safety factor for vertical bearing capacity
Extreme design contact stress at the footing bottom is assumed the form:
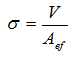
where:
V extreme design vertical force
Aef effective area of foundation
Effective Area
When solving the problem of eccentrically loaded foundations the program offers two options to deal with an effective dimension of the foundation area:
•a rectangular shape of effective area is assumed
•circular shape of effective area is assumed
Rectangular shape
A simplified solution is used in such cases. In case of axial eccentricity (bending moment acts in one plane only) the analysis assumes a uniform distribution of contact stress σ applied only over a portion of the foundation l1, which is less by twice the eccentricity e compared to the total length l.

Determination of effective area in case of axial eccentricity
An effective area (b*l1) is assumed to compute the contact stress, so that we have:
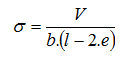
In case of a general eccentric load (foundation is loaded by the vertical force V and by bending moments M1 and M2 the load is replaced by a single force with given eccentricities:
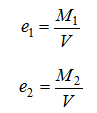
The size of effective area follows from the condition that the force V must act eccentrically:
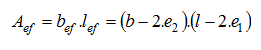
Circular shape
A circular foundation subjected to a vertical load applied with an eccentricity e=Md/Nd can be regarded as an equivalent fictitious foundation with a centrally applied load (Figure), as suggested by Meyerhof (1953) and Vesic (1973). In this case,the area of the fictitious foundation, A', can be calculated as:
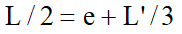
The aspect ratio of the equivalent rectangular area can also be approximated as the ratio of the line lengths b to l, as shown in Figure that is,
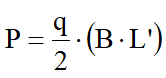
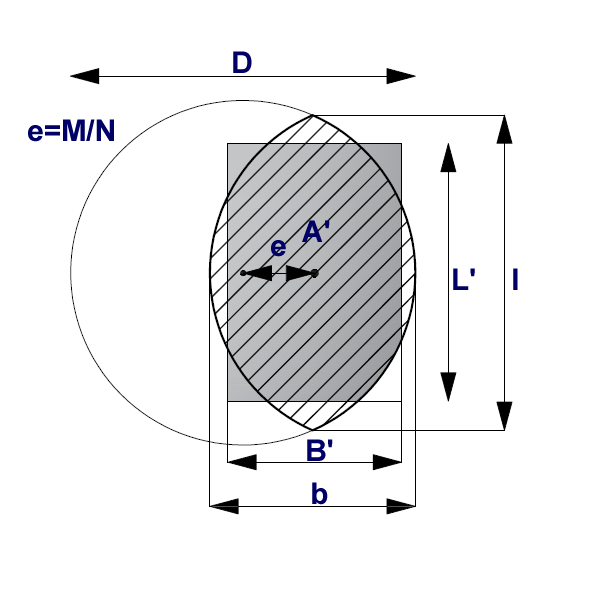
Método de cálculo de las dimensiones equivalentes de una cimentación sometida a carga no baricéntrica