Geophysics observes the behavior of waves propagating within a material. A seismic signal, in fact, changes according to the characteristics of the crossed environment. The waves can be generated artificially through the use of hammers, explosions, etc.
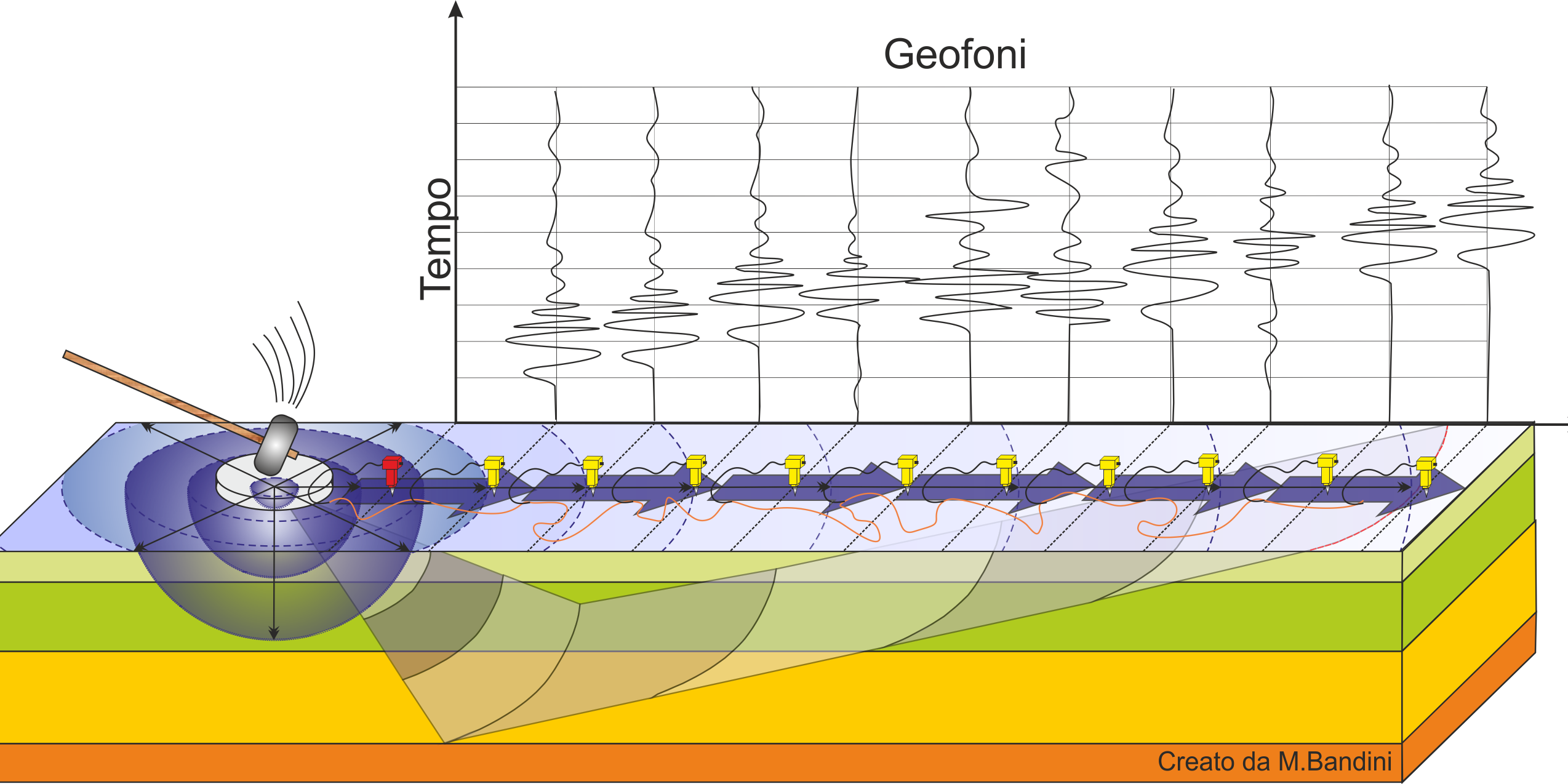
Motion of the seismic signal
The seismic signal can be decomposed into several phases, each of which identifies the movement of particles invested by the seismic waves. The phases are:
•Longitudinal-P: deep wave of compression;
•Transversal-S: deep wave of shear;
•Love-L: surface wave, composed of P and S waves;
•Rayleigh-R: surface wave consists of an elliptical and retrograde movement.
Rayleigh – “R” waves
In the past, studies on the spread of seismic waves have focused on the propagation of deep waves (P, S) considering surface waves as a disturbance of the seismic signal to analyze. Recent studies have allowed creating advanced mathematical models for the analysis of surface waves in environments with different stiffness.
Signal analysis with MASW technique
According to the fundamental hypothesis of the linear physics (Fourier's Theorem) signals can be represented as the sum of independent signals, called harmonics of the signal. These harmonics, for one-dimensional analysis, are trigonometric functions sine and cosine, and act independently, not interacting with each other. Focusing on each harmonic component, the final result in linear analysis will be equivalent to the sum of partial behaviors corresponding to different harmonics. The Fourier analysis (FFT spectral analysis) is the fundamental tool for the spectral characterization of the signal. The analysis of Rayleigh waves, using MASW technique is performed with the spectral treatment of the signal in the transformed domain, where you can, quite easily, identify the signal for the Rayleigh waves from other types of signals, observing in addition, the Rayleigh waves propagate with a velocity that is in function of the frequency. The velocity frequency link is called dispersion spectrum. The dispersion curve identified in the f-k domain is called the experimental dispersion curve, and in that domain represents the maximum amplitudes of the spectrum.
Modelling
From a synthetic geotechnical model characterized by thickness, density, Poisson's ratio, S and P wave velocity it is possible to simulate the theoretical dispersion curve, which links velocity and wavelength according to the correlation:
![]()
By changing the parameters of the synthetic geotechnical model, it can be obtained an overlay of the theoretical dispersion curve with the experimental one: this is called inversion and is used to determine the profile of velocities in environments with different stiffness.
Vibration modes
Both in the theoretical and experimental inversion curve it is possible to identify the different configurations of vibration of the ground. The modes for the Rayleigh waves can be: deformation in contact with the air, almost no deformation of the half-wavelength and zero deformation at high depths.
Depth of investigation
The Rayleigh waves decay at a depth approximately equal to the wavelength. Small wavelengths (high frequencies) are used to investigate superficial areas and large wavelengths (low frequencies) allow investigations to a greater depth.
© Geostru