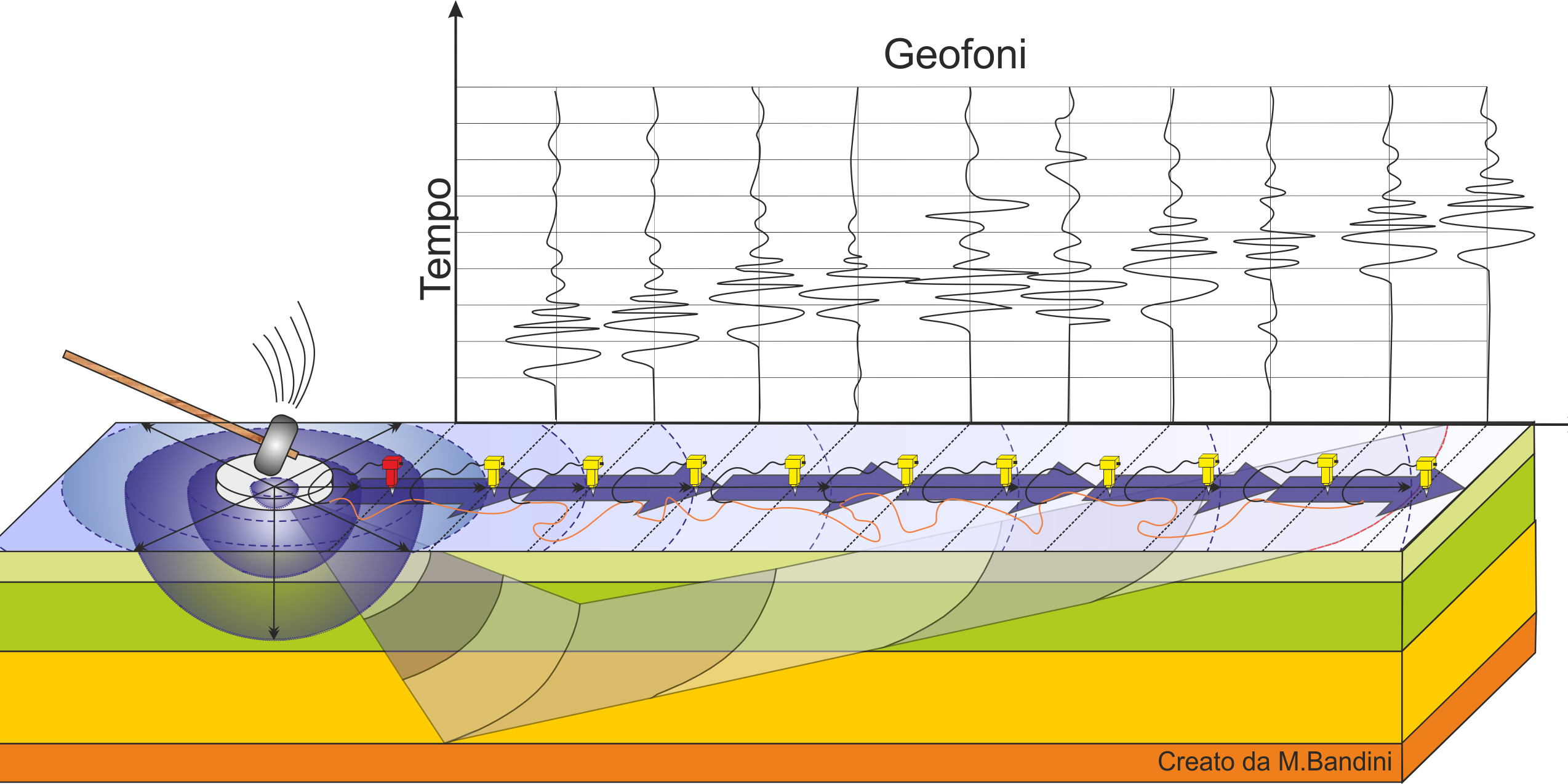
La geofísica analiza el comportamiento de las ondas que se propagan al interno de un material. De hecho, las señales sísmicas se modifican en función de las características del medio que atraviesan. Dichas ondas se pueden generar artificialmente usando martillo, explosivo, etc.
Movimiento de la señal sísmica
La señal sísmica se puede descomponer en varias fases, cada una de las cuales identifica el movimiento de las partículas embestidas por las ondas sísmicas. Las fases pueden ser:
•P - Longitudinal: onda profunda de compresión;
•S - Transversal: onda profunda de corte o de cizalla;
•L - Love: onda de superficie, compuesta por ondas P y S;
•R - Rayleigh: onda de superficie con movimiento en forma de elipse retrógrada.
Ondas de Rayleigh – “R”
En el pasado, los estudios sobre la difusión de las ondas sísmicas se han centrado en la propagación de las ondas profundas (P,S), considerando las ondas superficiales como un disturbo de la señal acústica a analizar. Recientes estudios han permitido crear modelos matemáticos avanzados para el análisis de las ondas de superficie en medios con distinta rigidez.
Análisis de la señal con técnica MASW
Según la hipótesis fundamental de la física lineal (Teorema de Fourier), las señales se pueden representar como la suma de señales independientes, llamadas armónicos de la señal. Dichos armónicos, por análisis monodimensional, son funciones trigonométricas seno y coseno y se comportan en modo independiente, sin interactuar entre sí. Concentrando la atención en cada componente armónico, el resultado final del análisis lineal será equivalente a la suma de los comportamientos parciales de cada armónico. El análisis de Fourier (Análisis espectral FFT) es el instrumento fundamental para la descomposición espectral de la señal.
El análisis de las ondas Rayleigh con la técnica MASW se lleva acabo mediante un tratamiento espectral de la señal que hace posible identificar con bastante facilidad la señal de las ondas Rayleigh con respecto a otros tipos de señales, teniendo en cuenta que las ondas Rayleigh se propagan a una velocidad que está en función de la frecuencia. Esta relación velocidad-frecuencia, que se conoce como espectro de dispersión, queda caracterizada en la llamada curva de dispersión, la cual se extrae mediante la transformada f-k y se conoce como curva de dispersión experimental y representa las amplitudes máximas del espectro en ese dominio.
Modelo
A partir de un modelo geotécnico sintético caracterizado por espesor, densidad, coeficiente de Poisson, velocidad de las ondas S y velocidad de las ondas P, es posible simular la curva de dispersión teórica que liga la velocidad y la longitud de onda según la relación:
![]()
Modificando los parámetros del modelo geotécnico sintético, se puede obtener una superposición de la curva de dispersión teórica con la experimental: esta fase se llama de inversión y permite determinar el perfil de las velocidades en medios con distintas rigideces.
Modos de vibración
Tanto en la curva de inversión teórica como en la experimental es posible identificar las diferentes configuraciones de vibración del terreno. Los modos de las ondas Rayleigh pueden ser: deformaciones en contacto con el aire, deformaciones casi nulas en la mitad de la longitud de onda y deformaciones nulas a grandes profundidades.
Profundidad del estudio
Las ondas Rayleigh decrecen en profundidades aproximadamente iguales a la longitud de onda. Pequeñas longitudes de onda (altas frecuencias) permiten estudiar zonas superficiales, mientras que grandes longitudes de onda (bajas frecuencias) permiten estudios a profundidades mayores.
© Geostru