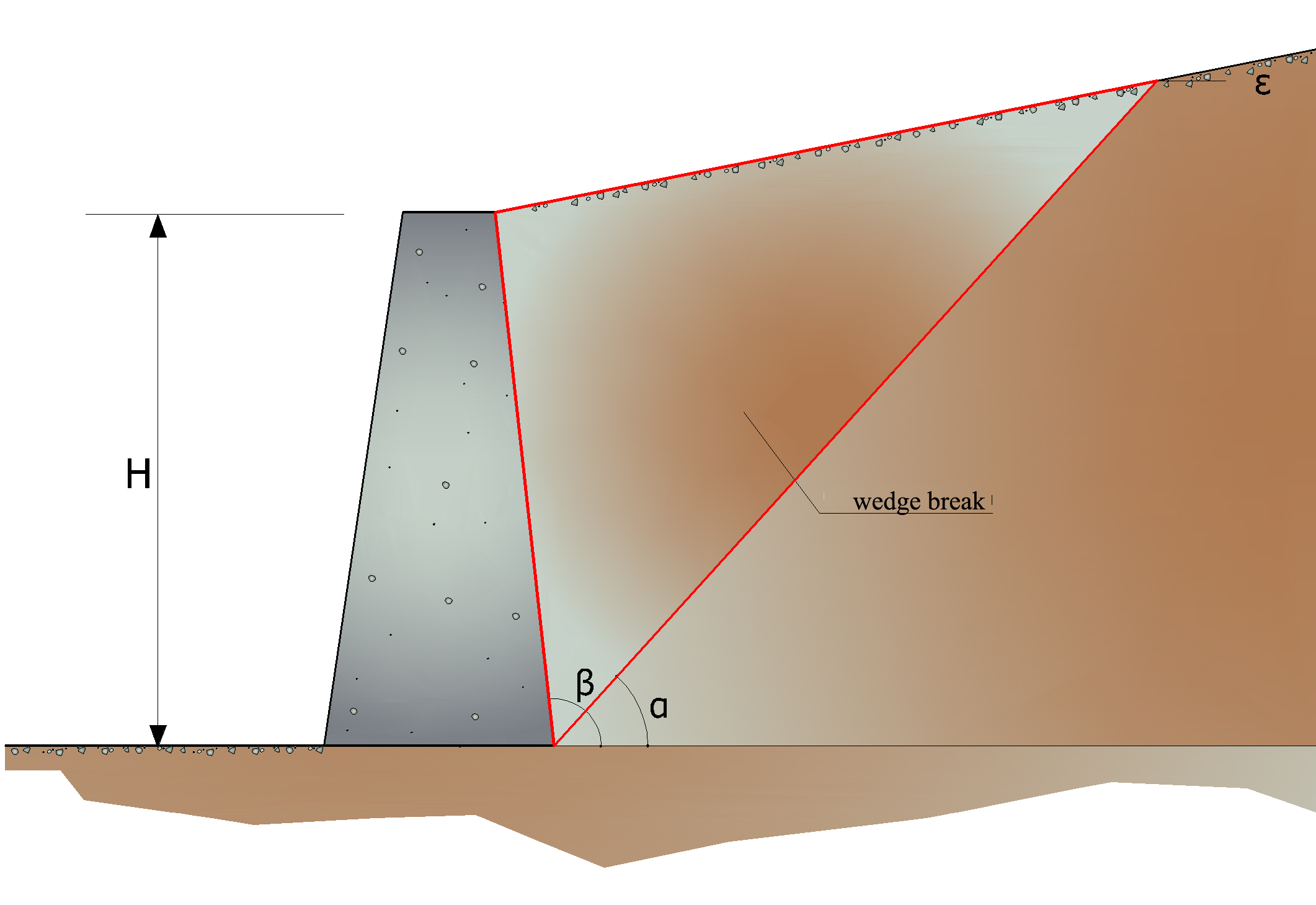
Active thrust calculation using Coulumb's method is based on global limit equilibrium theory of a system whose components are the wall and the wedge of homogeneous terrain behind the work assuming rough surface.
Where terrain is dry and homogeneous the pressure diagram is expressed linearly by the following:
Pt = Ka γt z
Thrust St is applied at 1/3 H with the value:
![]()
Having:
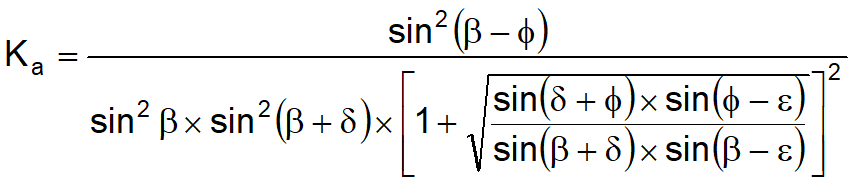
Limit value of Ka:
δ < (β-φ-ε) according to Muller-Breslau
γt = Terrain unit volume weight;
β = Inside wall surface inclination to horizontal plane of footing;
φ= Terrain shear resistance angle;
δ = Angle of friction terrain to wall;
ε = Field level inclination to horizontal - Positive if anticlockwise;
H = Wall height.
Active thrust calculation according to Rankine
If ε = δ = 0 e β= 90° (wall with smooth surface and backfill with horizontal surface) thrust St is simplified to:
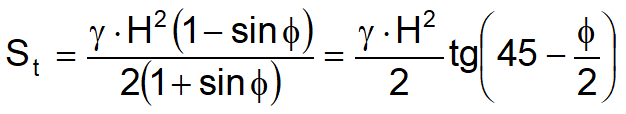
that coincides with Rankine's equation that gives active thrust where backfill is horizontal.
Effectively Rankine used the same hypothesis as Coulumb except that he ignored wall-terrain friction and cohesion. Rankine's expression for Ka in general form is as follows:
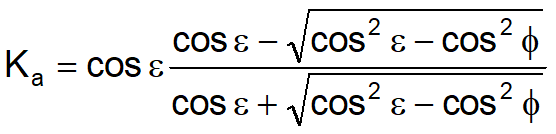
Active thrust calculation according to Mononobe & Okabe
Mononobe & Okabe's evaluation of active thrust concerns thrust in seismic states with pseudo static method. This is based on global limit equilibrium theory of a system whose components are the wall and the wedge of homogeneous terrain behind the work in an artificial configuration in which both field level inclination and the angle b - inclination of internal wall surface to horizontal -are increased by an amount q such that:
tgδ = kh/(1±kv)
where kh is the horizontal seismic coefficient and kv the vertical.
Where no specific studies exist coefficients kh & kv should be calculated as:
kh = S×ag/r kv = 0,5 kh
where S×ag is the maximum seismic acceleration in the various categories in the stratigraphic profile.
Factor r can take the value 2 where the work is one of some flexibility (e. g. gravity walls). In all other cases (Stiff concrete walls, On piles, Fixed head)) it should be set to 1.
Effect due to cohesion
Cohesion introduces negative constant pressures as:
![]()
As it is not possible to calculate a priori the thrust reduction caused by cohesion a critical height Zc has been calculated as:
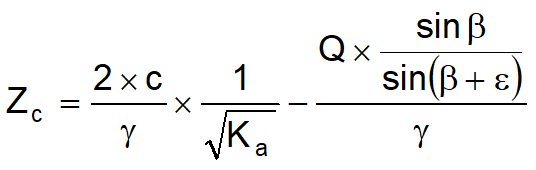
where:
Q = Loads acting on the backfill.
If Zc<0 the effect may be applied directly as a decrease whose value is:
Zc = Pc × H
applied at H/2.
Uniform load on backfill
A load Q, uniformly distributed on the backfill generates constant pressures as:
Pq = KaQ·senβ/sen(β+ε)
Integrating, a thrust Sq:
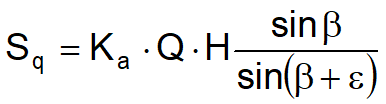
Applies at H/2, indicating as Ka the Muller-Breslau active thrust coefficient.
Active thrust in seismic state
In seimic state the calculation force exercised by the backfill on the wall is given by:
![]()
where:
H= wall height
kv= vertical seimic coefficient
γ = terrain unit volume weight
K = total thrust coefficient (static + dynamic)
Ews = hydrostatic water thrust
Ewd = hydrodynamic thrust
For impermeable terrains, hydrodynamic thrust Ewd = 0, but a correction on evaluation of the angle q in Mononobe & Okabe's formula is made as follows:
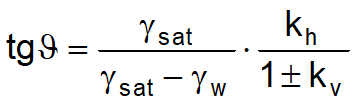
In highly permeable terrain in seismic states, the same correction is applied but hydrodynamic thrust assumes the following value:
![]()
where H' is the height of the groundwater tables(Gwt) from the base of the wall.
Hydrostatic thrust
Gwt whose surfac is at height Hw from the base of the wall generates hydrostatic pressures normal to its surface that at depth z are expressed as:
Pw(z) = γw· z
Resulting as:
Sw = 1/2 ·γw· H²
Thrust of submeged terrain can be obtained substituting γt con γ't(γ't = γsaturo - γw), effective weight of submerged material.
Passive resistance
In homogeneous terrain a linear diagram of pressures results:
Pt = Kp· γt· z
integrating with passive thrust:
![]()
having:
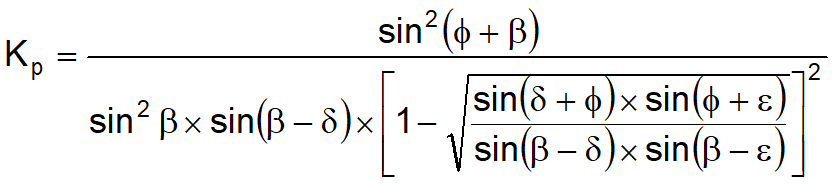
(Muller-Breslau) with d limit values at:
δ< β-φ-ε
The expression for Kp according to Rankine assumes the following form:

|
© Geostru