Criterio di Vesic
Secondo questo autore per tenere conto del fenomeno della dilatanza nel calcolo della capacità portante è sufficiente diminuire di 2° l’angolo d’attrito degli strati di fondazione. Il limite di questo suggerimento è nel fatto che non tiene conto dell’intensità della sollecitazione sismica (espressa attraverso il parametro dell’accelerazione sismica orizzontale massima). Questo criterio pare però trovare conferma nelle osservazioni fatte in occasione di diversi eventi sismici.
Criterio di Sano
L’autore propone di diminuire l’angolo d’attrito degli strati portanti di una quantità data dalla relazione:
![]()
dove Amax è l’accelerazione sismica orizzontale massima.
Questo criterio, rispetto a quello di Vesic, ha il vantaggio di prendere in considerazione anche l’intensità della sollecitazione sismica. L’esperienza però dimostra che l’applicazione acritica di questa relazione può condurre a valori eccessivamente cautelativi di Qlim.
Le correzioni di Sano e di Vesic si applicano esclusivamente a terreni incoerenti ben addensati. È errato applicarle a terreni sciolti o mediamente addensati, dove le vibrazioni sismiche producono il fenomeno opposto a quello della dilatanza, con aumento del grado di addensamento e dell’angolo d’attrito.
Momenti cinematici
In presenza dell'azione sismica la risposta del palo è il risultato di una complessa interazione terreno-palo, resa di difficile inerpretazione a causa dei fenomeni di non linearità nel terreno e degli effetti cinematici associati al moto del terreno.
Generalmente, alle sollecitazioni trasmesse dalla sovrastuttura si aggiungono, applicando il principio di sovrapposiszione degli effetti, quelle derivanti dall' interazione cinematica che produce nei pali sollecitazioni aggiuntive dipendenti principalmente dalla rigidezza relativa palo-terreno.
Dalla letteratura esistente in merito a questo tipo di studi, emerge che nel caso di palo immerso in terreni stratificati, la sollecitazione flettente subisce un pronunciato incremento in prossimità dell'interfaccia fra strati di differente rigidezza e tale incremento è tanto maggiore quanto più elevato è il contrasto di rigidezza. In alcuni casi il valore del momento prodotto da questo effetto potrebbe superare quello che insorge nei pali in testa in presenza di incastro.
Da un'analisi di numerosi risultati, Nikolaou et al., 2001, ha proposto una relazione che consente di calcolare , in maniera approssimata, il momento flettente massimo in corrispondenza dell'interfaccia tra due strati di differente rigidezza, in condizioni di moto stazionario con frequenza prossima alla frequenza fondamentale del deposito in cui è immerso il palo:
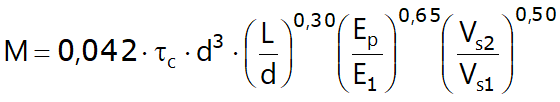
in cui τc = amax,s ρ1h1; Vs1 e Vs2, rispettivamente, la velocità delle onde di taglio nei due strati; E1 è modulo di rigidezza dello strato superiore di terreno.
I momenti valutati secondo l'espressione di Nikolaou sono indicati nella sezione Int. cinematica presente in Calcolo Strutturale.
© GeoStru