GENERACIÓN DE UN ACELEROGRAMA
Modelo del movimiento sísmico
La acción sísmica que se manifiesta en un sitio cualquiera se puede caracterizar en modo completo cuando se conoce la historia temporal de las aceleraciones, las velocidades y los desplazamientos del suelo.
Evidentemente este conocimiento tan detallado no se puede obtener basándose solo en parámetros macrosísmicos, como son la magnitud M y la posición focal R.
De hecho estas dos medidas, además de ser de naturaleza físico-empírica (a diferencia de las medidas que de ellas se derivan, las cuales son completamente físicas), no distinguen las particularidades entre los diferentes mecanismos que pueden generar un evento sísmico.
Además de esto, el efecto local está profundamente influenciado por las condiciones geológicas y morfológicas de la porción de corteza que atraviesan las ondas y por las condiciones estratigráficas y geotécnicas propias del sitio.
Por otro lado, con los conocimientos actuales, estos dos parámetros macrosísmicos son los únicos con los cuales se puede obtener un grado de información concreta utilizable en el análisis de riesgo sísmico.
Para lograr definir el movimiento sísmico local es definitivamente necesario valerse de esquemas simplificados en los cuales los parámetros macrosísmicos se integren con informaciones de naturaleza empírica (elaboraciones estadísticas de registros de sismos anteriores) o, a falta de ello, con elementos basados en consideraciones apropiadas de los datos específicos del problema: distancia de las fuentes potenciales, características locales del suelo, etc.
Un modelo simplificado del movimiento sísmico local (por ej. de la historia temporal de las aceleraciones), pero adecuado a un buen número de situaciones concretas, se representa con la expresión:
(1) a(t) = a×∑ Cn cos (ωn× t-ϕ n)
donde:
a representa el parámetro de intensidad y con más precisión, el valor de pico de la aceleración del suelo. Se trata de una variable aleatoria cuya distribución es obtenible en función de la aleatoriedad de la magnitud M y de la distancia focal R.
Los términos Cn son los coeficientes del desarrollo en la sumatoria de Fourier normalizados. Describen el contenido de frecuencia del movimiento en cuando dan la importancia relativa de los diferentes componentes elementales de frecuencia ωn. El diagrama de los coeficientes Cn en función de las frecuencias ωn representa el espectro de Fourier del evento sísmico considerado.
Los coeficientes Cn se normalizan en modo tal que la sumatoria de la segunda parte de (1) tenga un valor máximo de 1, resultando:
⎜a(t)⎜max=a
de acuerdo con la definición de a:
Los términos ωn=n2π⎜D son las pulsaciones (en rad/s) de los diferentes componentes armónicos, múltiplos de la frecuencia mínima: ω1=2π/D, siendo D la duración de la vibración.
Los términos ϕn son los ángulos de fase, uno por cada componente armónico, comprendidos entre 0 y 2π.
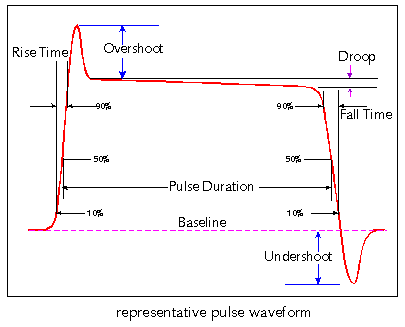
Rise Time
Tiempo para alcanzar el máximo de la aceleración.