In the present typology "rectangular section of column" (selected in General data Tab) you can check the instability of the column with two different simplified methods:
1- Nominal curvature method (§5.8.8 EC2). This method is primarily suitable for isolated member ('DCL' ductility) with constant normal force and defined length l0 (to be pre-calculated by the user according to § 5.8.3.2 EC2). The applicability of the method is limited to uniaxial bending
2- 'Model column method' based based on the tracing of the moment-curvature diagram. This method is applicable for both uniaxial and biaxial bending.
The input windows for this calculation is as follows:
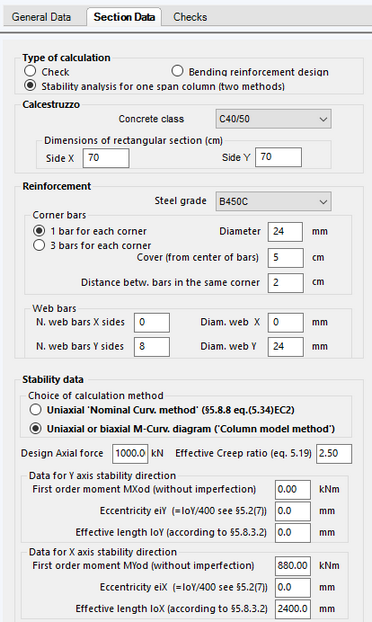

The relevant input data in this window are:
- Dimension of side X and Y of the concrete rectangular section
- Concrete Class and Steel grade
- Number and diameter and cover of corner bars and web bars
- Design constant axial force Nd
- Effective creep ratio according to eq. (5.19) EC2: φef = φ(∞,t0) MX0qp/MX0d where MX0qp is the first order moment in SLS quasi-permanent combination
- First order bending moment in ULS combination of interest: MX0d
- Eccentricity eY: = l0Y/400 to take into account geometric imperfections according to simplified alternative in § 5.2(9) EC2.
- Effective length l0Y: to evaluate in advance according to § 5.8.3.2 EC2
The curvature 1/r0 in eq (5.34)EC2 can be assessed by the program (see in above figure the option "Mode of calculation of curvature 1/r") with the direct formula in § 5.8.8.3 EC2 or by means the moment-curvature diagram as in "model column" method. In biaxial bending it is difficult to use the direct formula (5.34) of § 5.8.8.3 EC2 as it is hard to meet the conditions of applicability (5.38a) and (5.38b) EC2. The biaxial moment-curvature diagram provided without problems by the program make always possible to check biaxial instability.
In the below results such a diagram is shown together with the windows of numerical results.
