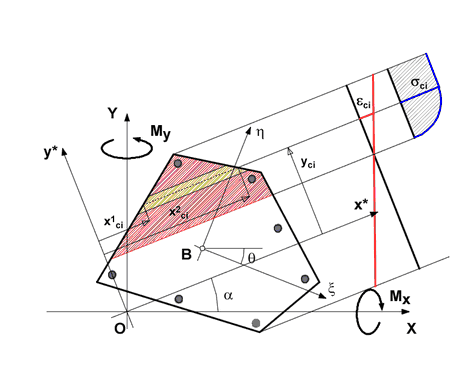
Si consideri la generica sezione di figura avente geometria e sforzi esterni riferiti al sistema X,Y generale di assi. Siano, inoltre ξ,η gli assi principali d’inerzia della sezione di solo calcestruzzo definiti dalle coordinate del baricentro B e dall’angolo θ formato dall’asse ξ con l’asse X.
A differenza del caso trattato nei precedenti paragrafi e relativo alle sole sollecitazioni rette, l’asse neutro di una qualsiasi deformazione ultima non è, in generale, parallelo all’asse X, formando con questo un angolo α. Al fine di utilizzare lo stesso tipo di integrazione numerica effettuata tramite la precedente espressione (5.5), si riferisce la sezione agli assi x*, y* ruotati di α ed aventi la stessa origine O. In questo sistema di riferimento l’asse neutro è sempre parallelo all’asse x* e ad esso sono ancora riferibili le sollecitazioni resistenti di cui alle (5.5), completate, in questo caso, dalla componente My*.
L’integrazione numerica può eseguirsi con le seguenti sommatorie:
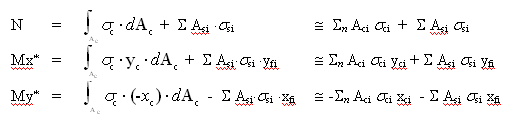 (1)
(1)
in cui, con riferimento alla generica striscia discreta i di figura si è posto:
Aci = (xci2- xci1) × Δy
(2)
xci = (xci2 + xci1) / 2
Le sollecitazioni flettenti resistenti vanno comunque riferite agli assi principali d’inerzia ξ, μ della sezione di solo calcestruzzo:
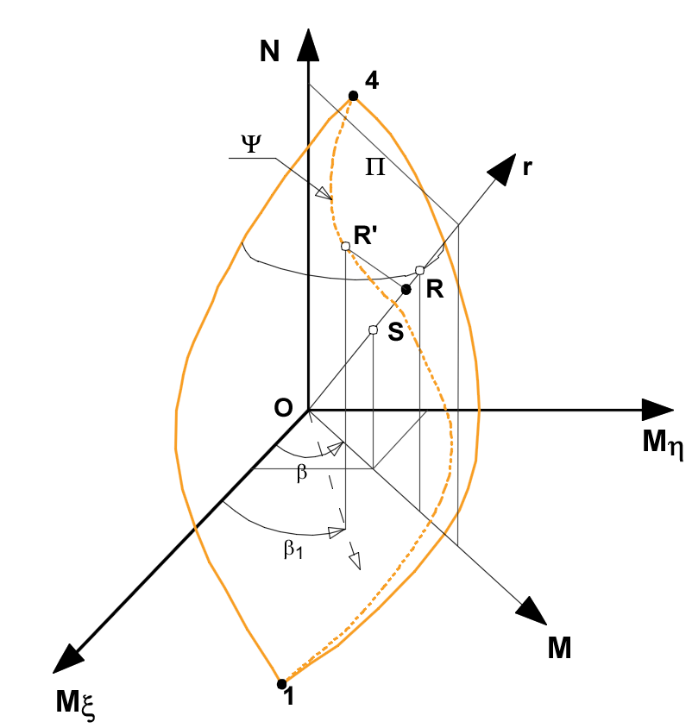
Fig.2
Mξ = Mx* cos θ + My* sin θ + N yR
Mη = -Mx* sin θ + My* cos θ - N xR
in cui con xR, yR sono indicate le coordinate dell’origine O riferite agli assi principali d’inerzia.
La generica sollecitazione esterna S, in definitiva, è caratterizzata in generale dalle tre componenti ⎨NSd, MηSd, MξSd⎬, che vanno confrontate, secondo una prefissata direzione r di misura, con le corrispondenti sollecitazioni resistenti R⎨NRd, MηRd, MξRd⎬ ottenute dall’intersezione della retta r con il dominio resistente, che in questo caso è racchiuso da una superficie di frontiera nelle tre dimensioni come indicato in Figura.
Ad ogni punto di questa superficie corrisponde una configurazione limite della sezione caratterizzata, cioè, dal raggiungimento della deformazione unitaria ultima da parte del calcestruzzo o dell’acciaio. In particolare i punti di cuspide 1 e 4, corrispondono alla massima deformazione della sezione a curvatura nulla rispettivamente per dilatazione e per accorciamento.
Si supponga adesso di bloccare la direzione dell’asse neutro (angolo α di fig. 1) facendo assumere alla deformata della sezione ( ε(y*) = b y*+ c ) gli stessi assetti limite descritti nel paragrafo relativo ai campi di rottura. L’applicazione delle (1) e poi delle (2) conduce alla determinazione di un insieme di punti ⎨N, Mξ ,Mη⎬, che costituiscono una determinata curva spaziale di interazione ψ, appartenente alla superficie di frontiera del generico dominio di resistenza, del tipo di quella rappresentata in figura. Tale curva di interazione spaziale è l’equivalente della curva piana tracciata per sollecitazioni rette.
Facendo variare l’angolo α (cioè la direzione dell’asse neutro) da 0 a 2 π e ripetendo le integrazioni si otterrebbe un fascio di curve di interazione ψ che nel loro insieme verrebbero a costituire l’intera superficie tridimensionale di interazione. Poiché tutte le curve ψ ammettono gli stessi assetti principali 1 e 4, esse iniziano e terminano tutte in tali punti di cuspide del dominio.
Si deve a questo punto osservare che per effettuare la verifica di una sezione in presso-tenso flessione deviata sarebbe eccessivamente oneroso, in termini di tempi di elaborazione, costruire per punti l’intero dominio resistente. Nel prossimo paragrafo viene, pertanto, sviluppata una strategia iterativa legata al metodo di misura della resistenza adottato, onde abbreviare drasticamente i tempi di verifica.
|
© 2023 Geostru Software