L'argomento è trattato estesamente nel § 4.5 delle CNR-DT 200 2013.
In sintesi l'avvolgimento del pilastro con sole fibre ortogonali all'asse del pilastro determina un aumento di resistenza. L'aumento di resistenza conseguibile è interessante solo nel caso di pilastri soggetti a compressione centrata o con piccola eccentricità in condizioni degradate o insufficienti a sopportare incrementi di solo sforzo normale: trattasi in questo caso di un intervento di riparazione locale (§ C8.4.1 Circolare NTC). Nel caso di pressoflessione con eccentricità sensibile l'incremento di resistenza è trascurabile (ma verrà comunque calcolata dal programma) mentre diventa importante l'incrementto di duttilità in curvatura che verrà trattata nel capitolo successivo (confinamento e duttilità).
In programma viene assunto il seguente diagramma tensioni deformazioni del calcestruzzo confinato con FRP simile ma semplificato ed a vantaggio di sicurezza rispetto a quello indicato nella figura 4-11 § 4.5.1 CNR2013, di seguito completata con i parametri assunti nel programma:
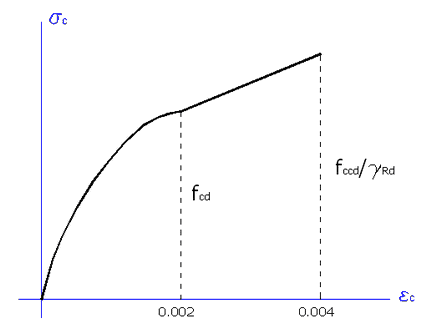
Fino al valore della deformazione assiale di 0.002 la tensione nel calcestruzzo confinato viene considerata uguale a quella del calcestruzzo non confinato, pur essendo in realtà leggermente superiore. Per deformazioni superiori a 0.002 e fino a 0.004 si modella il legame come lineare fino al raggiungimento della della massima resistenza da confinamento di calcolo pari a fccd come valutata nel seguito ridotta a mezzo del coeff. parziale γRd = 1.10 di cui alla formula (4.30) delle CNR2013. Si ricorda di evitare di superare il numero di 5 strato sovrapposti di tessuto.
Incremento di resistenza a compressione centrata (o con piccola eccentricità) § 4.5.2 CNR2013
In questo caso si tratta di valutare l'incremento di resistenza allo sforzo assiale in presenza di avvolgimento del tessuto FRP intorno al pilastro con le fibre disposte ortogonalmente all'asse del pilastro stesso. Se in input si assegna um momento flettente piccolo in confronto allo sforzo normale di progetto (cioè una piccola eccentricità) il programma va eseguito settando nei dati generali il percorso di sollecitazione ad eccentricità costante in modo da determinare così il massimo sforzo normale NRcc,d sviluppato grazie alla presenza del confinamento (ed in assenza di momento flettente).
La massima resistenza del calcestruzzo fccd viene valutata con la (4.31) nel § 4.5.2 CNR2013:
fccd = fcd (1+2.6(fl,eff/fcd)2/3)
in cui:
fl,eff = keff · fl = pressione di confinamento efficace: deve essere fl,eff / fcd > 0.05 altrimenti il confinamento non viene considerato efficace
keff = kH · kV · kα = coeff. efficienza (≤1) valutato con le formule del § 3.5.2.1 LG2009
fl = 0.5 rf · Ef · εfd,rid = pressione di confinamento valutata con le formule dei § 4.5.2.1 CNR2013
εfd,rid = min {ηa · εfk/γf ; 0.004} (4.37)CNR2013
L'applicazione diretta della (4.30)CNR2013:
NRcc,d = 1/γRd Ac fccd + As fyd
consente di cogliere subito il valore massimo dello sforzo normale resistente dopo il confinamento. Lanciando il programma è comunque possibile dedurre dai risultati del calcolo il valore fccd ed applicare direttamente la (4.30).
Incremento di resistenza a compressione eccentrica (con forte eccentricità)
In questo caso nel programma viene utilizzato lo stesso diagramma tensioni deformazioni sopra illustrato ma il calcolo, che in questo caso è necessariamente rivolto alla resistenza a flessione (nei dati generali va, di conseguenza, selezionato il percorso di sollecitazione a sforzo normale costante), conduce ad incrementi del momento flettente ultimo di poco superiore a quello ottenuto senza il confinamento con FRP.
Di seguito si riporta il grafico di output di un pilastro rettangolare in presso flessione deviata con piccola eccentricità con relativo diagramma qualitativo (in azzurro) delle tensioni ultime.
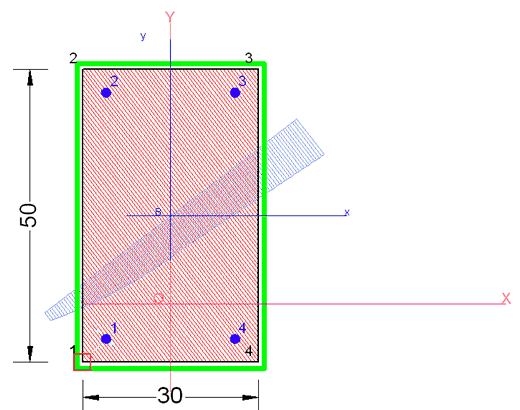
Di seguito si riporta la stampa dei dati di input e dei risultati numerici per la sezione di cui trattasi. In particolare per il tessuto FRP vengono riportati tutti i principali parametri di resistenza calcolati attraverso le formule delle LG2009.
DATI GENERALI SEZIONE IN C.A.
NOME SEZIONE: Compressione_FRP_rd.sezfrp
(Percorso File: C:\Programmi\Microsoft Visual Studio\VB98\RC_SEC_FRP_NEW\PROVE_NEW\Compressione_FRP_rd.sezfrp)
Descrizione Sezione:
Tipologia sezione iniziale: Sezione generica
Normativa di riferimento: N.T.C.
Percorso sollecitazione: A rapporto M/N costante
Riferimento Sforzi assegnati: Assi x,y principali d'inerzia sezione iniziale
Riferimento alla sismicità: Zona non sismica
Posizione sezione nell'asta: In zona nodale (di estremità)
CARATTERISTICHE DI RESISTENZA DEI MATERIALI IMPIEGATI
CALCESTRUZZO - Sezione iniziale: Rck250
Resist. di calcolo fcd: 113.30 daN/cm²
Deform. alla max resistenza epc0: 0.0020
Def.unit. ultima epcu: 0.0035 daN/cm²
Legge tensione-deformaz.: Parabola-Rettangolo
Modulo Elastico Normale Ec: 299600 daN/cm²
Resis. media a trazione fctm: 22.10 daN/cm²
Coeff. Viscosità post-rinforzo (solo S.L.E.) : 0.00
Resist. confinata max (al max parabola): 113.30 daN/cm²
Resist. confinata alla deform. ultima: 169.53 daN/cm²
Deformazione confinata alla max resistenza Epc0: 0.0020
Deformazione confinata ultima Epcu: 0.0040 daN/cm²
ACCIAIO - Barre Sez. Iniziale Tipo: Feb44k
Resist. caratt. snervam. fyk: 4300.0 daN/cm²
Resist. caratt. rottura ftk: 4300.0 daN/cm²
Resist. snerv. di calcolo fyd: 3739.0 daN/cm²
Resist. ultima di calcolo ftd: 3739.0 daN/cm²
Deform. ultima di calcolo Epu: 0.036
Modulo Elastico Es 2000000 daN/cm²
Legge tensione-deformaz.: Bilineare finito
FRP - In Tessuto o lamine per CONFINAMENTO: FRP_1
Calcolo secondo LG2009 = Linee guida del Dip. prot. civile(Sett. 2009)
Fattore convers. EtaA per Applic. TIPO A ($2.5.1 LG2009) 0.950
Modulo elastico ridotto Ef (coeff.rid.= AfE ex $5.3 LG2009): 2350000 daN/cm²
Resist. caratt. rottura ridotta ffk (coeff.rid.= Aff ex $5.3 LG2009): 28000 daN/cm²
Deform. caratt. a rottura e_fk= ffk/Ef 0.0119
Deform. a rottura per calcolo resistenza (formula [3.18]LG2009) 0.0040
Deform. a rottura per calcolo curvature (formula [3.44]LG2009) 0.0071
Lunghezza ottimale di ancoraggio Le (formula [3.1]LG2009) 163 mm
Spessore tf singolo strato tessuto/lamina 0.17 mm
Numero strati tessuto/lamina 3
Raggio di curvatura rc (>=20 mm) spigoli sezione cls. 20 mm
Coeff. efficienza orizzontale kH ([3.42] LG2009) 0.376
Coeff. efficienza verticale kV ([3.36] LG2009) 0.0053
Percentuale geometrica di rinforzo Ro_f ([3.39]/[3.41]LG2009): 8.3 %
Pressione laterale efficace di confinamento f1,eff ([3.33]LG2009): 9.4 daN/cm²
Resistenza calcestruzzo confinato fccd([3.32]LG2009): 169.5 daN/cm²
Deform. ultima calcestruzzo confinato nel calcolo di resistenza : 0.004
Resist. calcestruzzo nel calcolo di duttilità ($3.5.3 LG2009): 113.3 daN/cm²
Deform. ultima calcestruzzo confinato nel calcolo di duttilità: 0.0093
CARATTERISTICHE DOMINIO CONGLOMERATO
DOMINIO SEZ. INIZIALE N° 1
Forma del Dominio: Poligonale
Classe Conglomerato: Rck250
N°vertice: X [cm] Y [cm]
1 -15.0 -10.0
2 -15.0 40.0
3 15.0 40.0
4 15.0 -10.0
DATI BARRE ISOLATE SEZ. INIZIALE (Acciaio Feb44k)
N°Barra X [cm] Y [cm] DiamØ[mm]
1 -11.0 -6.0 16
2 -11.0 36.0 16
3 11.0 36.0 16
4 11.0 -6.0 16
SFORZI DI ESERCIZIO PRESENTI ALL'ATTO DEL RINFORZO
Sforzo normale [daN] preesistente applicato nel baricentro 0
Momento flettente Mx [daNm] preesistente al rinforzo 0
Momento flettente My [daNm] preesistente al rinforzo 0
ST.LIM.ULTIMI - SFORZI FINALI PER OGNI COMBINAZIONE ASSEGNATA
Gli sforzi sono quelli finali comprensivi di quelli preesistenti al rinforzo.
N Sforzo normale in daN applicato nel Baric. (+ se di compressione)
Mx Coppia concentrata in daNm applicata all'asse x princ. d'inerzia
con verso positivo se tale da comprimere il lembo sup. della sez.
My Coppia concentrata in daNm applicata all'asse y princ. d'inerzia
con verso positivo se tale da comprimere il lembo destro della sez.
Vy Componente del Taglio [daN] parallela all'asse princ.d'inerzia y
Vx Componente del Taglio [daN] parallela all'asse princ.d'inerzia x
N°Comb. N Mx My Vy Vx
1 50000 1000 500 0 0
2 50000 -1000 -500 0 0
RISULTATI DEL CALCOLO
Sezione verificata per tutte le combinazioni assegnate
METODO AGLI STATI LIMITE ULTIMI - RISULTATI PRESSO-TENSO FLESSIONE
Ver S = combinazione verificata / N = combin. non verificata
N Sforzo normale assegnato [daN] (positivo se di compressione)
Mx Momento flettente assegnato [daNm] riferito all'asse x princ. d'inerzia
My Momento flettente assegnato [daNm] riferito all'asse y princ. d'inerzia
N ult Sforzo normale ultimo [daN] nella sezione (positivo se di compress.)
Mx ult Momento flettente ultimo [daNm] rif. asse x princ. d'inerzia (tra parentesi Mx ult. sez. iniz.)
My ult Momento flettente ultimo [daNm] rif. asse y princ. d'inerzia (tra parentesi My ult. sez. iniz.)
Mis.Sic. Misura sicurezza = rapporto vettoriale tra (N ult,Mx ult,My ult) e (N,Mx,My)
Verifica positiva se tale rapporto risulta >=1.000
N°Comb Ver N Mx My N ult Mx ult My ult Mis.Sic.
1 S 50000 1000 500 198929 (177730) 3985 (3559) 1976 (1769) 3.979
2 S 50000 -1000 -500 198929 (177730) -3985 (-3559) -1976 (-1769) 3.979
METODO AGLI STATI LIMITE ULTIMI - DEFORMAZIONI UNITARIE ALLO STATO ULTIMO
ec max Deform. unit. massima del conglomerato a compressione
ec 3/7 Deform. unit. del conglomerato nella fibra a 3/7 dell'altezza efficace
Xc max Ascissa in cm della fibra corrisp. a ec max (sistema rif. X,Y,O sez.)
Yc max Ordinata in cm della fibra corrisp. a ec max (sistema rif. X,Y,O sez.)
es max Deform. massima in compressione nell'acciaio (negativa se di trazione)
Xs max Ascissa in cm della barra corrisp. a ef max (sistema rif. X,Y,O sez.)
Ys max Ordinata in cm della barra corrisp. a ef max (sistema rif. X,Y,O sez.)
es min Deform. minima in trazione nell'acciaio (positiva se di compress.)
Xs min Ascissa in cm della barra corrisp. a ef min (sistema rif. X,Y,O sez.)
Ys min Ordinata in cm della barra corrisp. a ef min (sistema rif. X,Y,O sez.)
N°Comb ec max ec 3/7 Xc max Yc max es max Xs max Ys max es min Xs min Ys min
1 0.00400 0.00216 15.0 40.0 0.00362 11.0 36.0 0.00070 -11.0 -6.0
2 0.00400 0.00216 -15.0 -10.0 0.00362 -11.0 -6.0 0.00070 11.0 36.0
POSIZIONE ASSE NEUTRO PER OGNI COMB. DI RESISTENZA
a, b, c Coeff. a, b, c nell'eq. dell'asse neutro aX+bY+c=0 nel rif. X,Y,O gen.
N°Comb a b c
1 0.000053815 0.000041383 0.001537458
2 -0.000053815 -0.000041383 0.002778949