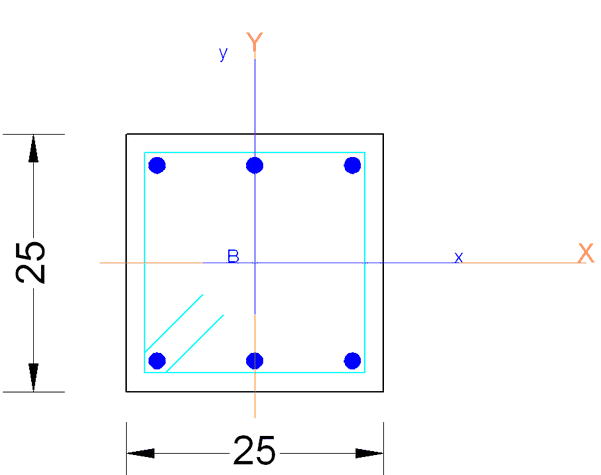
E' lo stesso pilastro esistente armato con 6Φ16 da rinforzare a solo sforzo normale già trattato nell'Esempio 2 mediante fasciatura con CFRP. Qui si vuole rinforzare il pilastro con una camicia in ca senza che le barre longitudinali della camicia si ancorino nei nodi (cioè la camicia in ca e le barre longitudinali non collaborano a presso flessione ma solo a taglio e confinamento). Nel caso del rinforzo con CFRP si è raggiunto lo sforzo normale richiesto di Ned = 105000 daN.
In assenza di confinamento l'applicazione della C4.1.13 NTC per pilasti con trascurabile eccentricità porterebbe ad una resistenza NRc = 0,8 Ac fcd + As fyd = 0,8 ⋅ 625 ⋅ 85 + 12 ⋅ 2739 = 75370 daN rispetto a quella richiesta di 105000 daN. In caso di confinamento con camicia è necessario valutare l'incremento di resistenza del calcestruzzo della sezione esistente (unico a resistere a sforzo normale unitamente alle barre esistenti) per effetto delle nuove staffe aggiunte nella camicia. Il riferimento per tale calcolo è costituito dalle formule del § 4.1.2.1.2.1 NTC considerando l'intera sezione esistente come nucleo confinato. Le formule ivi contenute (dalla (4.1.8) in poi) fanno però riferimento alla resistenza caratteristica fck che non è di facile determinazione nel caso di un calcestruzzo esistente. Nel programma ad fck si è sostituito il valore medio di fcm/FC con Fc fattore di conoscenza, trattandosi di comportamento duttile del materiale in presenza di confinamento.
RINFORZO CA
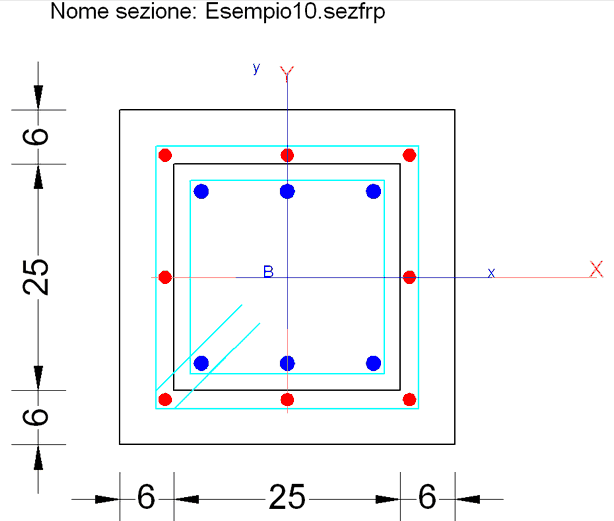
Il rinforzo è costituito essenzialmente da staffe Φ 10/5 cm B450C di confinamento, mentre la camicia dello spessore di 6 cm e le barre longitudinali qui non rivestono alcuna funzione statica se quella di collegare le nuove staffe al pilastro esistente. Per meglio confinare le staffe è importante vincolare le staffe alle barre intermedie sui lati mediante forcine che penetrino nel calcestruzzo del vecchio pilastro.
INPUT PERCORSO DI CARICO E SFORZI APPLICATI
Per cogliere lo sforzo normale massimo sopportabile è anzitutto necessario effettuare un calcolo di resistenza utilizzando il percorso di carico a eccentricità costante (nella scheda Dati generali).
Le NTC impongono una eccentricità minima ai pilastri essenzialmente compressi pari a 2 cm (o L/200 con L lungh. pilastro). In questo caso pertanto è necessario assegnare oltre allo sforzo normale il momento che esso sviluppa per una eccentricità di 2 cm.
RISULTATI
Per il rinforzo proposto la verifica è soddisfatta se non si superano i seguenti sforzi (si è operato per tentativi): N= 96000 daN e Mx = 96000x0.02 = 1920 daNm.
Detto valore risulta ben superiore a quello in assenza di rinforzo (75730) prima determinato.
I dati di input e di output sono tutti contenuti nella seguente relazione di calcolo da cui si può rilevare che ad es. la resistenza confinata del calcestruzzo è pari a 133.2 daN/cm².
Naturalmente è possibile variare i dati delle staffe confinanti a seconda delle esigenze del calcolo.
DATI GENERALI SEZIONE IN C.A.
NOME SEZIONE: Esempio10.sezfrp
(Percorso File: C:\L\SORGENTI2017\RC-SEC-FRP-2017\ESEMPI\Esempio10.sezfrp)
Descrizione Sezione: Esempio2 Lenci 281
Tipologia sezione iniziale: Sezione rettangolare di pilastro
Lato X sezione [cm]: 25.0
Lato Y sezione [cm]: 25.0
Normativa di riferimento: C8A.7.1 NTC
Percorso sollecitazione: A rapporto M/N costante
Riferimento Sforzi assegnati: Assi x,y principali d'inerzia sezione iniziale
Riferimento alla duttilità Deformazione materiali fino a rottura
Posizione sezione nell'asta: In zona nodale (di estremità)
CARATTERISTICHE DI RESISTENZA DEI MATERIALI IMPIEGATI
CALCESTRUZZO - Sezione iniziale pre-rinforzo: fck150
Modulo Elastico secante Ecm: 258926 daN/cm²
Fattore di Confidenza FC assunto: 1.35
Resistenza media a compressione fcm: 172.13 daN/cm²
Resistenza caratteristica del calcestruzzo: 150.00 daN/cm²
Resistenza di progetto (senza confinam.) fcd: 85.00 daN/cm²
Deform. unitaria alla max resistenza (senza confinam.) epc0: 0.0020
Deform. unitaria ultima (senza confinam.) epcu: 0.0035 daN/cm²
Legge tensione-deformaz.: Parabola-Rettangolo
Modulo Elastico secante Ecm: 258926 daN/cm²
Resist. confinata max (al max parabola): 133.24 daN/cm²
Resist. confinata alla deform. ultima: 133.24 daN/cm²
Deformazione confinata alla max resistenza Epc0: 0.0049
Deformazione confinata ultima Epcu: 0.0389 daN/cm²
CALCESTRUZZO - Classe cls. camicia: fck150
Spessore camicia c.a.: 6.0 cm
Modulo Elastico secante Ecm: 258926 daN/cm²
Resistenza media a compressione fcm: 172.13 daN/cm²
Resistenza caratteristica del calcestruzzo: 150.00 daN/cm²
Resistenza di progetto (senza confinam.) fcd: 85.00 daN/cm²
Deform. unitaria alla max resistenza (senza confinam.) epc0: 0.0020
Deform. unitaria ultima (senza confinam.) epcu: 0.0035 daN/cm²
Legge tensione-deformaz.: Parabola-Rettangolo
Modulo Elastico secante Ecm: 258926 daN/cm²
ACCIAIO - Barre Sez. Iniziale pre-rinforzo Tipo: Feb32k
Fattore di Confidenza FC assunto: 1.00
Resistenza media a snervamento = fym : 3150.0 daN/cm²
Resist. media a rottura = ftm : 3622.5 daN/cm²
Resist. a snervamento di progetto fyd=fym/(FC*1.15): 2739.0 daN/cm²
Rapporti: ftm/fym = ftk/fyk : 1.15
Deform. unitaria ultima di progetto Epu: 0.036
Modulo Elastico Es 2000000 daN/cm²
Legge tensione-deformaz.: Bilineare finito
ACCIAIO - Barre di rinforzo Tipo: B450C
Resistenza media a snervamento fym (per duttilità): 5175.0 daN/cm²
Resistenza media a rottura ftm (per duttilità): 5951.3 daN/cm²
Resistenza caratteristica a snervamento fyk: 4500.0 daN/cm²
Resistenza a snervamento di progetto fyd: 3913.0 daN/cm²
Resistenza a rottura di progetto ftd: 3913.0 daN/cm²
Rapporti: ftm/fym = ftk/fyk : 1.15
Deform. unitaria ultima di progetto Epu: 0.068
Modulo Elastico Es 2000000 daN/cm²
Legge tensione-deformaz.: Bilineare finito
CARATTERISTICHE DOMINIO CONGLOMERATO
DOMINIO SEZ. INIZIALE N° 1
Forma del Dominio: Poligonale
Classe Conglomerato: fck150
N°vertice: X [cm] Y [cm]
1 -12.5 -12.5
2 -12.5 12.5
3 12.5 12.5
4 12.5 -12.5
DATI BARRE ISOLATE SEZ. INIZIALE (Acciaio Feb32k)
N°Barra X [cm] Y [cm] DiamØ[mm]
1 -9.5 -9.5 16
2 -9.5 9.5 16
3 9.5 9.5 16
4 9.5 -9.5 16
5 0.0 -9.5 16
6 0.0 9.5 16
DATI GENERAZIONI LINEARI DI BARRE SEZ. INIZIALE
N°Gen. Numero assegnato alla singola generazione lineare di barre
N°Barra Ini. Numero della barra iniziale cui si riferisce la generazione
N°Barra Fin. Numero della barra finale cui si riferisce la generazione
N°Barre Numero di barre generate equidistanti cui si riferisce la generazione
Ø Diametro in mm delle barre della generazione
N°Gen. N°Barra Ini. N°Barra Fin. N°Barre Ø
1 1 4 1 16
2 2 3 1 16
DATI NUOVE BARRE DI RINFORZO (Acciaio B450C)
N°Barra X [cm] Y [cm] DiamØ[mm]
1 -13.5 -13.5 14.0
2 -13.5 13.5 14.0
3 13.5 13.5 14.0
4 13.5 -13.5 14.0
5 -13.5 0.0 14.0
6 13.5 0.0 14.0
7 0.0 -13.5 14.0
8 0.0 13.5 14.0
SFORZI DI ESERCIZIO PRESENTI ALL'ATTO DEL RINFORZO
Sforzo normale [daN] preesistente applicato nel baricentro 78000
Momento flettente Mx [daNm] preesistente al rinforzo 0
Momento flettente My [daNm] preesistente al rinforzo 0
ST.LIM.ULTIMI - SFORZI FINALI PER OGNI COMBINAZIONE ASSEGNATA
Gli sforzi sono quelli finali comprensivi di quelli preesistenti al rinforzo.
N Sforzo normale [daN] applicato nel Baric. (+ se di compressione)
Mx Coppia concentrata [daNm] applicata all'asse x princ. d'inerzia
con verso positivo se tale da comprimere il lembo sup. della sez.
My Coppia concentrata [daNm] applicata all'asse y princ. d'inerzia
con verso positivo se tale da comprimere il lembo destro della sez.
Vy Componente del Taglio [daN] parallela all'asse princ.d'inerzia y
Vx Componente del Taglio [daN] parallela all'asse princ.d'inerzia x
N°Comb. N Mx My Vy Vx
1 96000 1920 0 0 0
RISULTATI DEL CALCOLO
Sezione verificata per tutte le combinazioni assegnate
METODO AGLI STATI LIMITE ULTIMI - RISULTATI PRESSO-TENSO FLESSIONE
Ver S = combinazione verificata / N = combin. non verificata
N Sforzo normale assegnato [daN] (positivo se di compressione)
Mx Momento flettente assegnato [daNm] riferito all'asse x princ. d'inerzia
My Momento flettente assegnato [daNm] riferito all'asse y princ. d'inerzia
N ult Sforzo normale ultimo [daN] nella sezione (positivo se di compress.)
Mx ult Momento flettente ultimo [daNm] rif. asse x princ. d'inerzia (tra parentesi Mx ult. sez. iniz.)
My ult Momento flettente ultimo [daNm] rif. asse y princ. d'inerzia (tra parentesi My ult. sez. iniz.)
Mis.Sic. Misura sicurezza = rapporto vettoriale tra (N ult,Mx ult,My ult) e (N,Mx,My)
Verifica positiva se tale rapporto risulta >=1.000
N°Comb Ver N Mx My N ult Mx ult My ult Mis.Sic.
1 S 96000 1920 0 97284 (86168) 1946 (0) 0 (0) 1.013
METODO AGLI STATI LIMITE ULTIMI - DEFORMAZIONI UNITARIE ALLO STATO ULTIMO
ec max Deform. unit. massima del conglomerato a compressione
Xc max Ascissa in cm della fibra corrisp. a ec max (sistema rif. X,Y,O sez.)
Yc max Ordinata in cm della fibra corrisp. a ec max (sistema rif. X,Y,O sez.)
es max Deform. massima in compressione nell'acciaio (negativa se di trazione)
Xs max Ascissa in cm della barra corrisp. a ef max (sistema rif. X,Y,O sez.)
Ys max Ordinata in cm della barra corrisp. a ef max (sistema rif. X,Y,O sez.)
es min Deform. minima in trazione nell'acciaio (positiva se di compress.)
Xs min Ascissa in cm della barra corrisp. a ef min (sistema rif. X,Y,O sez.)
Ys min Ordinata in cm della barra corrisp. a ef min (sistema rif. X,Y,O sez.)
N°Comb ec max Xc max Yc max es max Xs max Ys max es min Xs min Ys min
1 0.03890 -12.5 12.5 0.03991 -13.5 13.5 -0.00690 -13.5 -13.5
POSIZIONE ASSE NEUTRO PER OGNI COMB. DI RESISTENZA
a, b, c Coeff. a, b, c nell'eq. dell'asse neutro aX+bY+c=0 nel rif. X,Y,O gen.
N°Comb a b c
1 0.000000000 0.001733891 0.017230349