Given a high demand for biaxial shear (as in seismic zones) we try in the following, to assess the effective area resistant to shear provided not only by hoops, but also by cross-ties actually arranged in the section with the same pitch of the brackets. It is assumed here that the variation of the direction of the shear force (as normally occurs in various combinations provided) results in a consequent change in the effective resistant area to shear provided by hoops and cross-ties.
To fix ideas, consider the generic section of a column, represented in the following figure, reinforced with two hoops marked A, B and two cross-ties a, b.

With reference to the perimetric hoop A we can say that, regardless of the direction of the shear, its contribution can always be assumed to be two times the area of the cross section of the hoop itself. The effectiveness of this hoop is indeed always maximal because it envelops in each case, the strut of the resistant truss at maximum depth for any direction of shear forces. Said maximum effectiveness may be commensurate to the maximum distance between the longitudinal bars (connected by hoop A) on the measured direction of the shear force (length h0 in the figure). For every shear direction it is always possible to identify two resistant legs of the hoop which develop an effective shear resistant area equal to two times the area of the section of the hoop.
The effective area of inner hoops (such as B) , can be evaluated by reducing the area of the two legs by means of a factor equal to the ratio h0'/ h0 in which h0' is the maximum distance between the bars enclosed by the inner hoop (always measured on the direction of the shear here assumed orthogonal to neutral axis).
With similar reasoning can be considered the effective area of the single cross-tie reduced to the ratio h0'' / h0 where h0'' is the projection of the length of the tie on the shear force direction. On the safe side we may exclude (in the calculation of effective area) the cross-ties in which at least one of the two ends does not fall in the compression zone of the section.
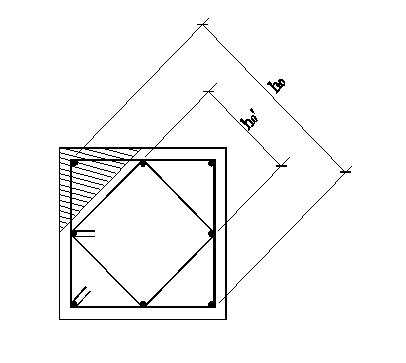
Consider, for example, the below square section transversely reinforced with two hoops, as well square, which steel bars have the same cross-sectional area Abr. With reference to a shear force inclined of 45° to the sides of the section, the effective area of the external perimeter hoop is equal to that of two legs: 2 Abr. As said above the effective area of the inner bracket can be assessed equal to:
2 Abr h0 '/ h0 = Abr.
In total, therefore, the effective area resistant to a shear vector angle of 45 ° is equal to 3 Abr .
In the case, instead, where the shear is parallel to the sides of the section, resulting h0 '= h0, we can assume as effective area 4 Abr. For all intermediate inclinations, therefore, the effective area of the transverse reinforcement to be taken in checks of ductility capacity and of shear resistance ranges from 3Abr to 4 Abr.