Le principali definizioni riguardanti l'analisi probabilistica di grandezze idrologiche con riferimento al modello TCEV sono riportate di seguito:
Stima puntuale
Stima xT del valore assunto da una grandezza idrologica in corrispondenza di un assegnato periodo di ritorno sulla base della serie campionaria della variabile x nel punto di interesse.
Stima regionale
Stima xT del valore assunto da una grandezza idrologica in corrispondenza di un assegnato periodo di ritorno utilizzando l'informazione fornita dalle serie storiche disponibili nella regione in cui si trova il punto di interesse.
Stima mista
Stima xT del valore assunto da una grandezza idrologica in corrispondenza di un assegnato periodo di ritorno ottenuta combinando l'informazione puntuale e quella regionale.
Modello probabilistico TCEV (two component extreme value) (1)
Il modello a doppia componente TCEV ipotizza che i valori estremi di una grandezza idrologica (portata, pioggia) facciano parte di due differenti popolazioni legate a differenti fenomeni meteorologici.
Alla base di questa ipotesi c'è il fatto che molte serie di massimi annuali presentano uno o più valori nettamente maggiori degli altri e tali da sembrare non provenienti dalla stessa popolazione degli altri dati.
L'espressione della CDF della distribuzione TCEV è data da
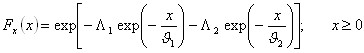
Nell'espressione precedente si sono indicati con il pedice 1 i parametri riguardanti la "componente base" e con il pedice 2 i parametri relativi alla "componente straordinaria".
I parametri Λ1 e Λ2 rappresentano il numero medio annuo di eventi indipendenti delle due componenti, mentre ϑ1 e ϑ2 esprimono il loro valore medio annuo.
La distribuzione TCEV equivale al prodotto di due distribuzioni di Gumbel, con la quale viene a coincidere se si pone Λ2=0.
Riferendosi alla variabile standardizzata:
![]()
si ha che la CDF di y è data da:
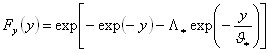
avendo posto:
![]()
La media della distribuzione TCEV è data dall'espressione:
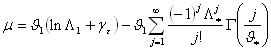
con γε=0,5772, costante di Eulero. Con il simbolo Γ si è indicata la funzione gamma:
![]()
Il coefficiente di variazione teorico dipende da Λ1, Λ* e ϑ* ed è quindi indipendente da ϑ1.
Il coefficiente di asimmetria teorico dipende da Λ* e ϑ* ed è quindi indipendente da Λ1 e ϑ1.
Distribuzione probabilistica TCEV: Modelli regionali
Il modello TCEV consente di costruire un modello regionale articolato in una struttura gerarchica.
Infatti si può assumere che esistano delle regioni in cui è costante il solo coefficiente di asimmetria e quindi siano costanti i parametri Λ* e ϑ* e delle sottoregioni di queste, più limitate, in cui sia costante pure il coefficiente di variazione e, quindi, il parametro Λ1.
Il primo livello di regionalizzazione consiste nell'individuare zone omogenee (ZO) nelle quali si può assumere che il coefficiente di asimmetria teorico delle serie dei massimi annuali sia costante. I parametri Λ* e ϑ* possono essere stimati utilizzando tutte le serie storiche disponibili nella zona, riducendo in modo consistente l'incertezza della stima.
Al secondo livello di regionalizzazione si individuano delle sottozone omogenee (SZO), con estensione minore rispetto alle precedenti, nelle quali oltre al coefficiente di asimmetria risulta costante anche il coefficiente di variazione. In una sottozona risultano quindi costanti i tre parametri Λ1, Λ* e ϑ*. Λ1 può quindi essere stimato in base a tutte le serie storiche ricadenti nella sottozona.
In una sottozona rimane costante la CDF di x/μ. Infatti dall'espressione della CDF della TCEV, introducendo i parametri Λ* e ϑ* si ha:
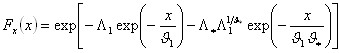
poiché si può scrivere:
![]()
e cioè:
![]()
avendo posto
![]()
e
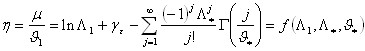
si ottiene:
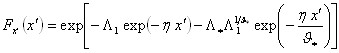
alla quale si dà il nome di curva di crescita.
Al terzo livello di regionalizzazione si individuano all'interno della sottozona omogenea le relazioni che intercorrono tra μ e le caratteristiche fisiche o climatiche dei bacini.
In definitiva la stima xT di una grandezza idrologica ad un prefissato tempo di ritorno può essere effettuata, in base al modello TCEV, in quattro modi diversi:
a) |
Al livello di regionalizzazione zero, in cui tutti i parametri del modello sono stimati dalla singola serie |
b) |
Al livello di regionalizzazione uno, in cui i parametri Λ* e ϑ* sono stimati a livello regionale e Λ1 e ϑ1 dalla singola serie |
c) |
Al livello di regionalizzazione due, in cui i parametri Λ*, ϑ* e Λ1 sono stimati a livello regionale e ϑ1 dalla singola serie |
d) |
Al livello di regionalizzazione tre, in cui tutti i parametri sono stimati con tecniche di analisi regionale |
|