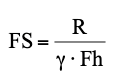De los resultados de la simulación numérica de impacto de una roca sobre una tierra reforzada se deducen:
Ek (energía de impacto)
Vk (velocidad cinética de impacto)
hk (altura típica de impacto)
Dado el volumen de la roca que se desprende, se determinan:
1.el lado de la marca en la tierra reforzada (se supone que la roca esté contenida en un cubo de lado "l"): l=(volumen de la roca)^0.3333
2.radio esférico equivalente: r=[3*volumen de la roca/(4*pi)]^0.3333
Otros datos de la roca:
P.u.v. [kN/m^3]
masa=[(P.u.v.)*volumen de la roca]/aceleración de la gravedad
A diferencia de las tierras reforzadas elásticas, un talud disipa la energía cinética del impacto de la roca a través del trabajo que la roca misma debe realizar para penetrar en la estructura de tierra.
Por lo tanto, se debe calcular la profundidad de penetración del bloque y verificar que sea inferior al espesor de la obra. En caso contrario, la construcción se considerará subdimensionada.
La profundidad de penetración puede evaluarse utilizando la relación de Kar (1978), en el caso de impacto directo con material terroso:
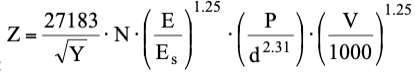
E = módulo de elasticidad de la roca [kJ]
Es = módulo elástico del acero [kJ]
Y = resistencia a la compresión simple del terreno [kPa]
N = factor de forma de la roca (1 para cuerpos puntiagudos, 0.72 para cuerpos planos)
V = velocidad de impacto de la roca [m/s]
d = radio esférico equivalente [cm]
P = peso de la roca [kg]
La profundidad de penetración es entonces:
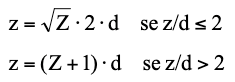
En la práctica, ya que hay dos posibles soluciones, se debe considerar el valor más grande y verificar que la respectiva condición z/d se cumpla. En caso contrario, se tomará como resultado válido el otro valor calculado. En caso de que el talud esté soportado arriba por un muro o por un gavión, la expresión de Z debe reescribirse de la siguiente manera:
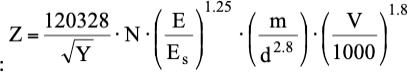
Si desde el cálculo de Z se concluye que la roca penetra a una profundidad mayor que el espesor del muro o del gavión, será necesario evaluar la velocidad residual del bloque de la siguiente forma:
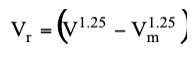
con
V= velocidad de impacto de la roca;
Vm = velocidad mínima necesaria para traspasar el muro o el gavión, que se puede calcular colocando el valor del espesor del muro en lugar del parámetro z (según la relación z/d resultante), determinando así Z y resolviendo la expresión con respecto a V.
Solamente entonces se puede obtener Z a partir de la siguiente expresión (sustituyendo V con Vr).
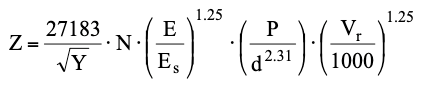
Cálculo de la fuerza impulsiva generada por el impacto
Hipótesis:
Comportamiento elasto-plástico del terreno que constituye el talud y de una carga dinámica variable en el tiempo.
La fuerza impulsiva máxima generada por la roca se puede calcular utilizando la relación de Mc Carty y Carden (1962).
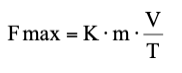
Fmax = fuerza impulsiva en [kgf]
K = constante generalmente fijada en 2.022
m = masa del bloque [kg]
V = velocidad de impacto de la roca [m/s]
T = duración del impacto [s]
Para determinar T, se puede utilizar la siguiente expresión:
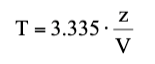
con
z = profundidad de penetración de la roca [m]
V = velocidad de impacto de la roca [m/s]
Prueba de deslizamiento
Bajo la hipótesis de que la roca impacte casi ortogonalmente a la fachada, la fuerza de impacto puede descomponerse en las dos direcciones ortogonales definidas por el sistema de referencia fijado de antemano.
El ángulo de incidencia que la dirección de la fuerza de impacto forma con el eje x se obtiene de la regla:
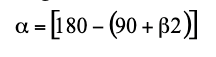
donde:
β2 representa el ángulo de inclinación del paramento a monte del talud.
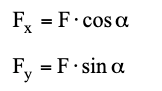
Dada la geometría de la estructura, es necesario evaluar el peso de la porción del talud que se opone al deslizamiento.
La longitud del plano de deslizamiento se determina mediante la relación:
Ls= 3·l
Con l lado de la marca sobre la tierra reforzada;
El ancho del plano de deslizamiento se determina mediante:
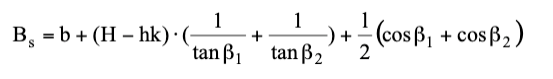
El peso de la porción del talud de tierra reforzada que se opone al deslizamiento será:
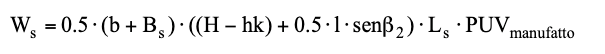
Es necesario verificar que la fuerza horizontal debido al impacto de la roca esté contrastado, con un correcto factor de seguridad, por la fuerza de fricción.
Para evaluar el componente cohesivo y de fricción que actúa sobre la superficie de deslizamiento, se aplica la siguiente relación:
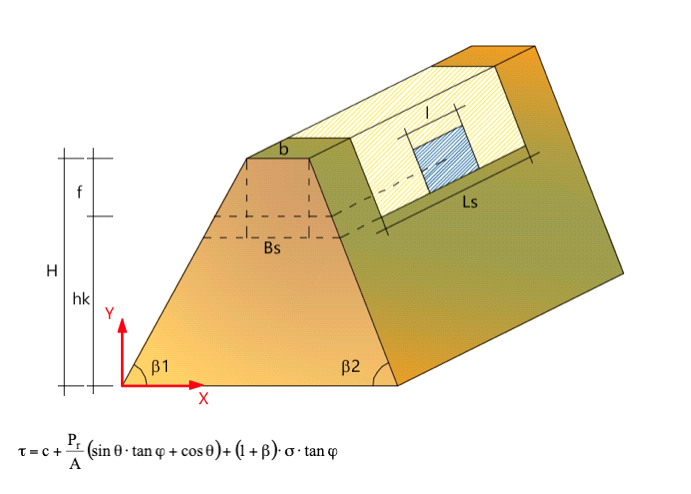
C = cohesión del suelo de relleno [kN/m²]
Pr = Resistencia a la tracción del refuerzo [kN]
A = Área del elemento de refuerzo [m²]
φ = ángulo de fricción interna del suelo de relleno
θ = se puede asumir 45 + φ/2
β = coeficiente que permite tener en cuenta la dilatación [0.2-0.4]
Sustituyendo Tallow por Pr y la espaciado de los refuerzos por A, se obtiene:
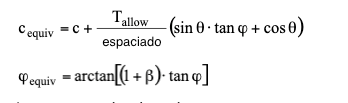
Las componentes resistentes serán:
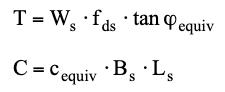
componente de fricción
componente cohesiva
La resistencia total es la suma de las dos componentes resistentes.
R = T + C
La verificación se realiza después de determinar el factor de seguridad.