Dai risultati dalla simulazione numerica di impatto di un masso su un rilevato paramassi si ricavano:
Ek (energia d'impatto)
Vk (velocità cinetica d'impatto)
hk (altezza caratteristica d'impatto)
Noto il volume del masso che si stacca, si determinano:
1.il lato dell'impronta sul rilevato paramassi (si ipotizza che il masso sia contenuto in un cubo di lato "l"): l=(volume del masso)^0.3333
2.raggio sferico equivalente: r=[3*volume del masso/(4*pi.greco())]^0.3333
Altri dati del masso:
P.u.v. [kN/m^3]
massa=[(P.u.v.)*volume masso]/accelerazione di gravità
A differenza delle barriere paramassi elastiche, un terrapieno dissipa l'energia cinetica d'impatto del masso attraverso il lavoro che il masso stesso deve compiere per penetrare nella struttura in terra. Va quindi calcolata la profondità di penetrazione del blocco roccioso e verificata che sia inferiore allo spessore dell'opera. In caso contrario il manufatto va considerato sottodimensionato.
La profondità di penetrazione può essere valutata con la relazione di Kar (1978), nel caso d'impatto diretto con il materiale terroso:
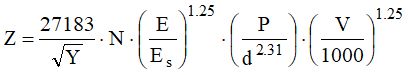
E=modulo elasticità della roccia [kJ]
Es=modulo elastico dell’acciaio [kJ]
Y=resistenza alla compressione semplice del terreno [kPa]
N=Fattore di forma del masso (1 per corpi appuntiti, 0.72 per corpi piatti)
V= velocità d’impatto del masso [m/s]
d= raggio sferico equivalente [cm]
P= peso del masso [kg]
La profondità di penetrazione è dunque:![]()
![]()
Nella pratica, vista la doppia soluzione possibile, andrà preso in considerazione il valore maggiore, e si dovrà verificare che la rispettiva condizione z/d sia rispettata. In caso contrario si assumerà come risultato valido l'altro valore calcolato. Nel caso il terrapieno sia sostenuto a monte da un muro o da una gabbionata l’espressione di Z va riscritta nel seguente modo:
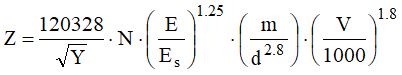
Se dal calcolo di Z risultasse che il masso penetra per una profondità superiore allo spessore del muro o della gabbionata, occorrerà valutare la velocità residua del blocco come segue
![]()
con
V = velocità d'impatto del masso;
Vm = velocità minima necessaria per attraversare il muro o la gabbionata, valutabile ponendo il valore dello spessore del muro al posto del parametro z (a seconda del rapporto z/d risultante), determinando quindi Z e risolvendo l’espressione rispetto a V.Solo a questo punto si può ottenere Z dalla seguente espressione (sostituendo V con Vr).
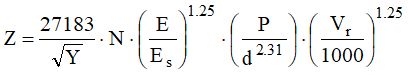
Calcolo della forza impulsiva generata dall'impatto
Ipotesi:
Comportamento elasto-plastico del terreno costituente il terrapieno e di un carico dinamico variabile nel tempo.
La forza impulsiva massima generata dal masso può essere calcolata con la relazione di Mc Carty e Carden (1962)
![]()
Fmax= forza impulsiva in [kgf]
K= costante posta generalmente pari a 2.022
m= massa del blocco [kg]
V = velocità d'impatto del masso [m/s]
T = durata dell’impatto [s]
Per determinare T si può utilizzare l’espressione :
![]()
con
z= profondità di penetrazione del masso [m]
V= velocità d'impatto del masso [m/s]
Verifica a scivolamento
Nell’ipotesi che il masso incida pressoché ortogonalmente alla facciata, la forza d’impatto può scomporsi nelle due direzioni ortogonali definiti dal sistema di riferimento fissato a priori.
L’angolo di incidenza che la direzione della forza d’impatto forma con l’asse delle x si ricava dalla regola:
![]()
dove :
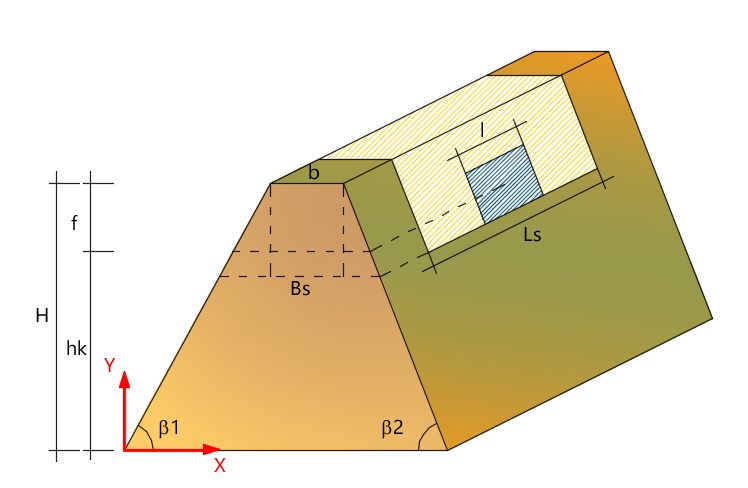
β2 rappresenta l’angolo di inclinazione del paramento di monte del terrapieno.
![]()
![]()
Nota la geometria dell’opera occorre valutare il peso della porzione di rilevato che si oppone allo scorrimento:
La lunghezza del piano di scivolamento si determina dalla relazione:![]()
Con l lato dell'impronta sul rilevato paramassi;
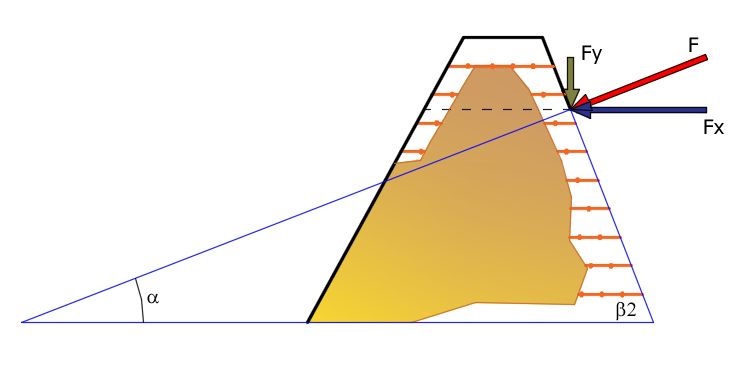
La larghezza del piano di scivolamento si determina da :
![]()
Il peso della porzione di rilevato che si oppone allo scorrimento sarà:
![]()
Occorre verificare che la forza orizzontale dovuta all’impatto del masso sia contrastata, con un adeguato fattore di sicurezza dalla forza di attrito.
Per valutare la componente coesiva ed attritiva che agisce sulla superficie di scorrimento si applica la seguente relazione:
![]()
C=coesione del terreno di riempimento [kN/mq]
Pr=Resistenza a trazione del rinforzo [kN]
A= Area dell’elemento di rinforzo [mq]
φ= angolo attrito interno del terreno di riempimento
θ= si può assumere 45+ φ/2
β= coefficiente che consente di tenere conto della dilatanza [0.2-0.4]
Si sostituisce alla Pr la Tallow e ad A la spaziatura dei rinforzi
Sostituendo tutti i valori si ottiene:
![]()
![]()
Le componenti resistenti saranno
![]() componente attritiva
componente attritiva
![]() componente coesiva
componente coesiva
La resistenza totale è la somma delle due componenti resistenti
![]()
La verifica viene eseguita dopo aver determinato il fattore di sicurezza
![]()