Il criterio di Mohr-Coulomb
Poiché la maggior parte del software geotecnico è ancora scritto in termini di criterio di rottura di Mohr-Coulomb, è necessario determinare angoli di attrito equivalenti e forze coesive per ogni ammasso roccioso ed intervallo di tensione. Ciò viene effettuato inserendo una relazione lineare media per la curva generata, risolvendo l’equazione 2 per un range di valori della tensione principale minore definiti da
![]()
come illustrato in figura 1.
Il processo di adattamento comporta il bilanciamento delle aree sopra e sotto il piano di Mohr-Coulomb. Ciò comporta le seguenti equazioni per l’angolo di attrito ![]() e la forza coesiva
e la forza coesiva ![]() :
:
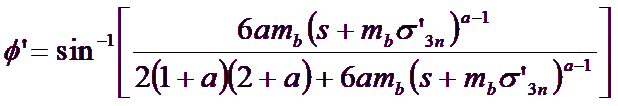 [12]
[12]
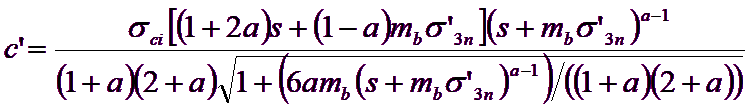 [13]
[13]
dove:
![]()
Si noti che il valore di ![]() , il limite superiore della tensione di confinamento sul quale la relazione tra il criterio di Hoek-Brown e quello di Mohr-Coulomb è considerata, deve essere determinato per ciascun caso individuale.
, il limite superiore della tensione di confinamento sul quale la relazione tra il criterio di Hoek-Brown e quello di Mohr-Coulomb è considerata, deve essere determinato per ciascun caso individuale.
La forza tangenziale di Mohr-Coulomb ![]() , per una data tensione normale
, per una data tensione normale ![]() , si ottiene dalla sostituzione di questi valori di
, si ottiene dalla sostituzione di questi valori di ![]() e
e ![]() nell’equazione:
nell’equazione:
![]() [14]
[14]
Il piano equivalente, in termini delle tensioni principali maggiore e minore, è definito da:
![]() [15]
[15]
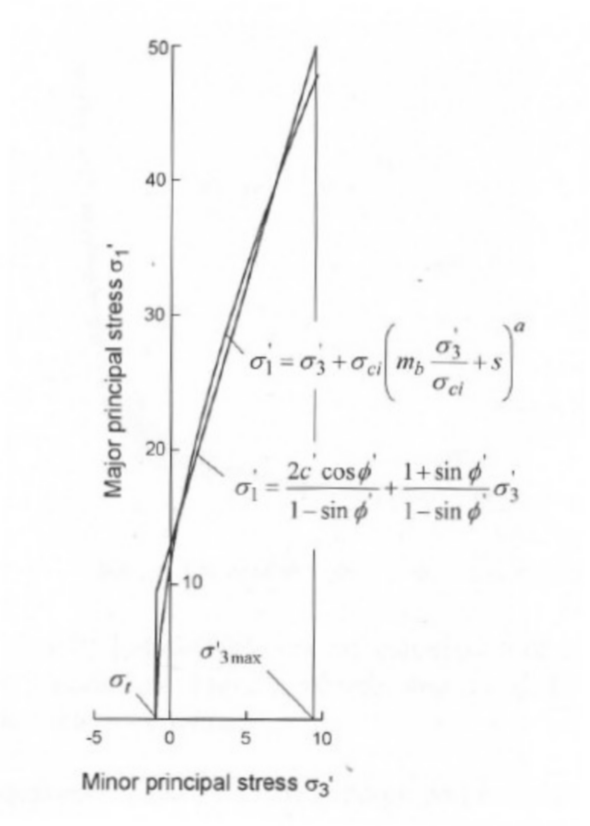
Figura 1: Relazioni tra le tensioni principali maggiore e minore per Hoek-Brown e il criterio equivalente di Mohr-Coulomb.
La resistenza dell’ammasso roccioso
La resistenza a compressione uniassiale dell’ammasso roccioso ![]() è dato dall’equazione 6. La rottura inizia al limite di uno scavo quando
è dato dall’equazione 6. La rottura inizia al limite di uno scavo quando ![]() viene superato dallo sforzo indotto da questo limite.
viene superato dallo sforzo indotto da questo limite.
La rottura si propaga da questo punto iniziale in un campo di tensione biassiale ed esso infine si stabilizza quando la resistenza locale, definita dall’equazione 2, è più alta delle tensioni indotte ![]() e
e ![]() . La maggior parte dei modelli numerici è in grado di seguire questo processo di propagazione della rottura e questo livello di analisi dettagliata è molto importante se si considera la stabilità di scavi in roccia e nella progettazione di sistemi di sostegno.
. La maggior parte dei modelli numerici è in grado di seguire questo processo di propagazione della rottura e questo livello di analisi dettagliata è molto importante se si considera la stabilità di scavi in roccia e nella progettazione di sistemi di sostegno.
Tuttavia, ci sono momenti in cui è utile prendere in considerazione il comportamento generale di un ammasso roccioso piuttosto che il processo di propagazione della rottura dettagliato di cui sopra. Per esempio, quando si considera la resistenza di un pilastro, è più utile avere una stima della resistenza complessiva del pilastro, piuttosto che una conoscenza dettagliata della misura della propagazione della frattura nel pilastro. Questo porta al concetto di "forza dell’ammasso roccioso" globale e Hoek e Brown hanno proposto che questa potrebbe essere stimata dalla relazione di Mohr-Coulomb:
![]() [16]
[16]
con ![]() e
e ![]() determinati per l’intervallo tensionale :
determinati per l’intervallo tensionale :
![]()
dando
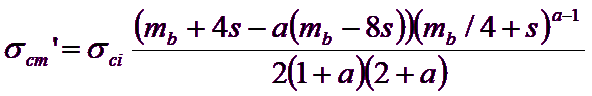 [17]
[17]
Determinazione di 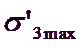
Il problema di determinare il valore appropriato di ![]() per l'utilizzo nelle equazioni 12 e 13 dipende dalla specifica applicazione. Due casi saranno studiati:
per l'utilizzo nelle equazioni 12 e 13 dipende dalla specifica applicazione. Due casi saranno studiati:
1. Gallerie - dove il valore di ![]() è quello che dà curve caratteristiche equivalenti per i due criteri di rottura per le gallerie profonde o profili di cedimento equivalenti per le gallerie superficiali.
è quello che dà curve caratteristiche equivalenti per i due criteri di rottura per le gallerie profonde o profili di cedimento equivalenti per le gallerie superficiali.
2. Pendii - quì il fattore di sicurezza calcolato e la forma e la localizzazione della superficie di rottura devono essere equivalenti.
Per il caso delle gallerie profonde, soluzioni in forma chiusa per entrambi i criteri Generalizzato di Hoek-Brown e di Mohr-Coulomb sono state utilizzate per generare centinaia di soluzioni e trovare il valore di ![]() che dà curve caratteristiche equivalenti.
che dà curve caratteristiche equivalenti.
Per gallerie superficiali, dove la profondità al di sotto della superficie è minore di 3 diametri di scavo, studi numerici comparativi della misura della rottura e il grado del cedimento della superficie hanno dato una relazione identica a ciò che è stato ottenuto per le gallerie profonde, a condizione che la speleologia in superficie è evitata.
I risultati degli studi per gallerie profonde sono rappresentati in Figura 2 e l’equazione inserita per entrambi i casi è:
 [18]
[18]
dove ![]() è la resistenza dell’ammasso roccioso, definita dall’equazione 17,
è la resistenza dell’ammasso roccioso, definita dall’equazione 17, ![]() è il peso per unità di volume dell’ammasso roccioso ed H è la profondità della galleria al di sotto della superficie. Nei casi in cui la tensione orizzontale è più alta di quella verticale, il valore della tensione orizzontale dovrebbe essere utilizzato al posto di
è il peso per unità di volume dell’ammasso roccioso ed H è la profondità della galleria al di sotto della superficie. Nei casi in cui la tensione orizzontale è più alta di quella verticale, il valore della tensione orizzontale dovrebbe essere utilizzato al posto di ![]() .
.
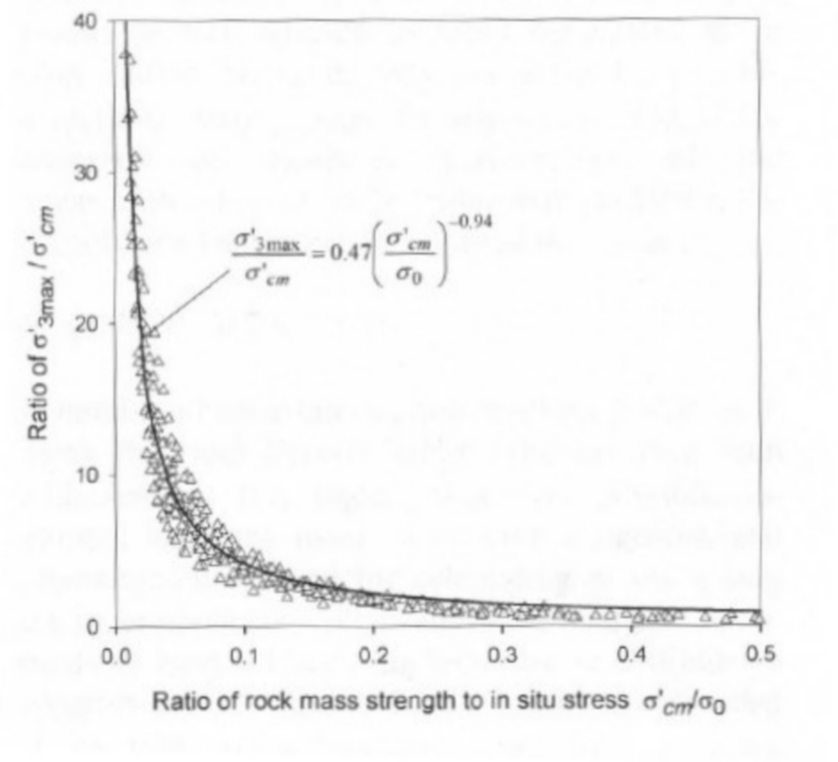
Figura 2: Relazione per il calcolo di ![]() per i parametri equivalenti di Mohr-Coulomb e Hoek-Brown per le gallerie.
per i parametri equivalenti di Mohr-Coulomb e Hoek-Brown per le gallerie.
L’equazione 18 si applica a tutti gli scavi sotterranei, che sono circondati da una zona di rottura che non si estende in superficie. Per studi su problematiche quali il blocco dello scavo nelle miniere è consigliabile che non si tenti di correlare i parametri di Hoek-Brown e di Mohr-Coulomb e che la determinazione delle proprietà del materiale e la successiva analisi siano basate su uno solo di questi criteri.
Studi analoghi per i pendii, usando l’analisi a rottura circolare di Bishop (1955) per un’ampia gamma di geometrie di pendi e proprietà di ammassi rocciosi hanno dato:
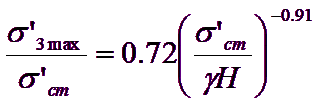 [19]
[19]
dove H è l’altezza del pendio.
© GeoStru