“Tratto da Elaborazioni probabilistiche idrologiche con Runoff Lab”
In questo articolo si propone un esempio applicativo di un'analisi idrologica condotta, utilizzando il software Elaborazioni idrologiche – Runoff Lab sviluppato da GeoStru. L'analisi consiste nel trattare statisticamente i dati storici registrati da alcune stazioni pluviometriche che gravitano nell'area del bacino del Fiume Esaro di Crotone.
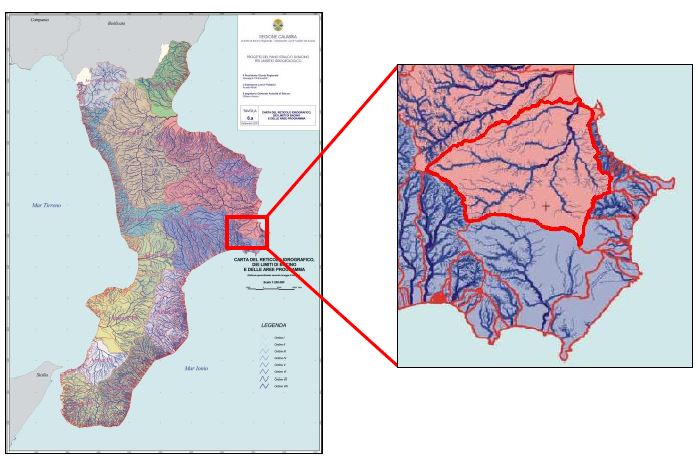
Fig. 1 - Individuazione geografico bacino Fiume Esaro Crotone
Le stazioni pluviometriche
I dati storici fanno riferimento alle seguenti 7 stazioni pluviometriche (ARPACAL – Centro Funzionali Multirischi)
•Crotone – Crepacuore (Codice: 1660);
•Crotone – Papanice (Codice: 1675);
•San Mauro Marchesato (Codice: 1740);
•Crotone – Salica (Codice: 1695);
•Cutro (Codice: 1670);
•Isola Capo Rizzuto (Codice: 1700);
•Crotone (Codice: 1680).
Dopo aver avviato il programma, sul menù di navigazione gerarchico, posizionato a sinistra rispetto all’area di lavoro (Fig.2), sono presenti gli strumenti necessari per condurre l'analisi idrologica:
•Stazioni di misura;
•Elaborazioni probabilistiche;
•Curve di pioggia;
•Pluviogrammi;
•Idrogrammi.
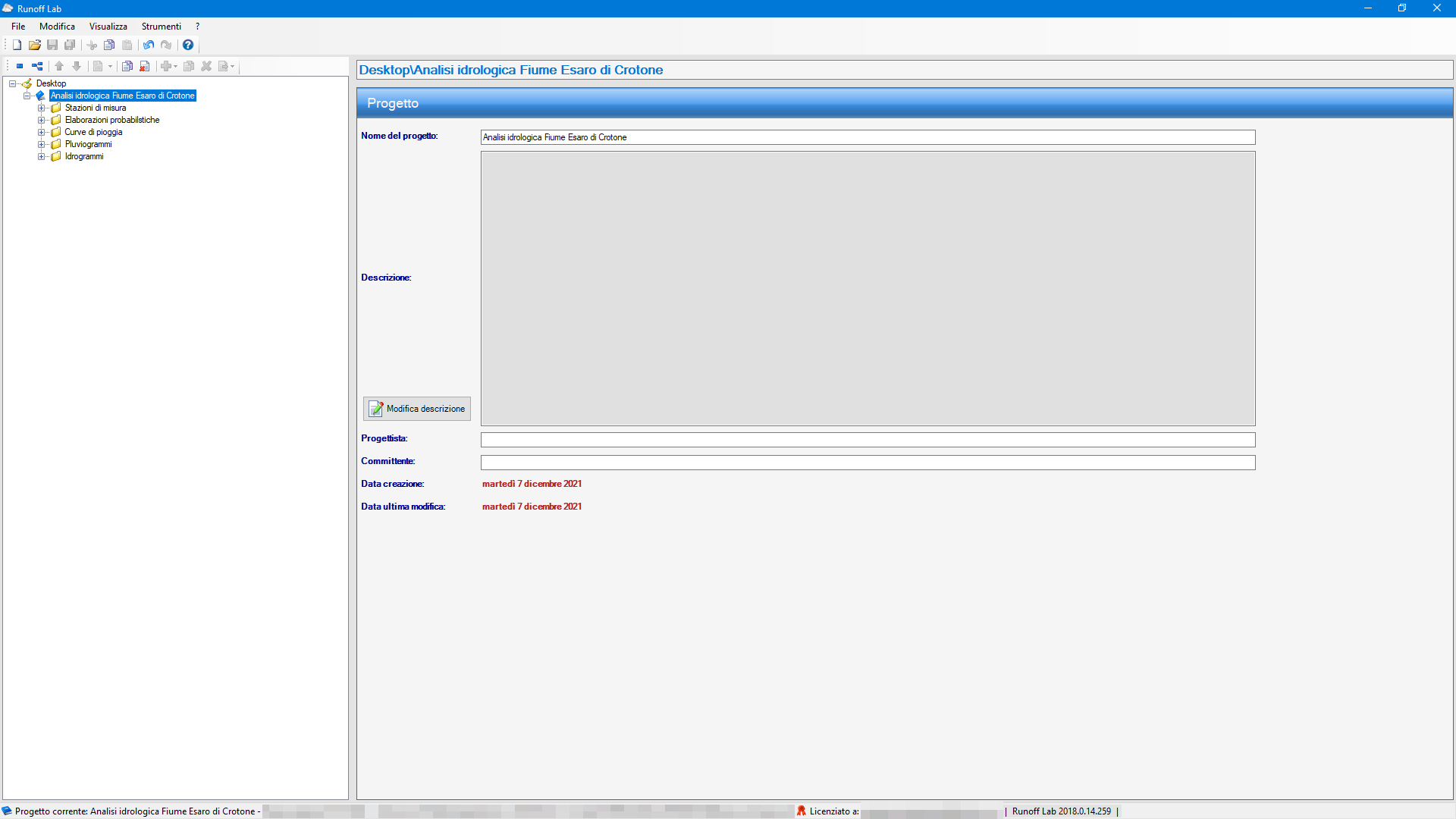
Figura 2 - Interfaccia Runoff Lab
L'analisi è stata condotta utilizzando le altezze massime di precipitazione oraria di durata 1, 3, 6, 12, 24 ore. Dopo aver creato la stazione di misura, le serie storiche verranno caricati digitando il comando “Aggiungi serie” (Fig. 3):
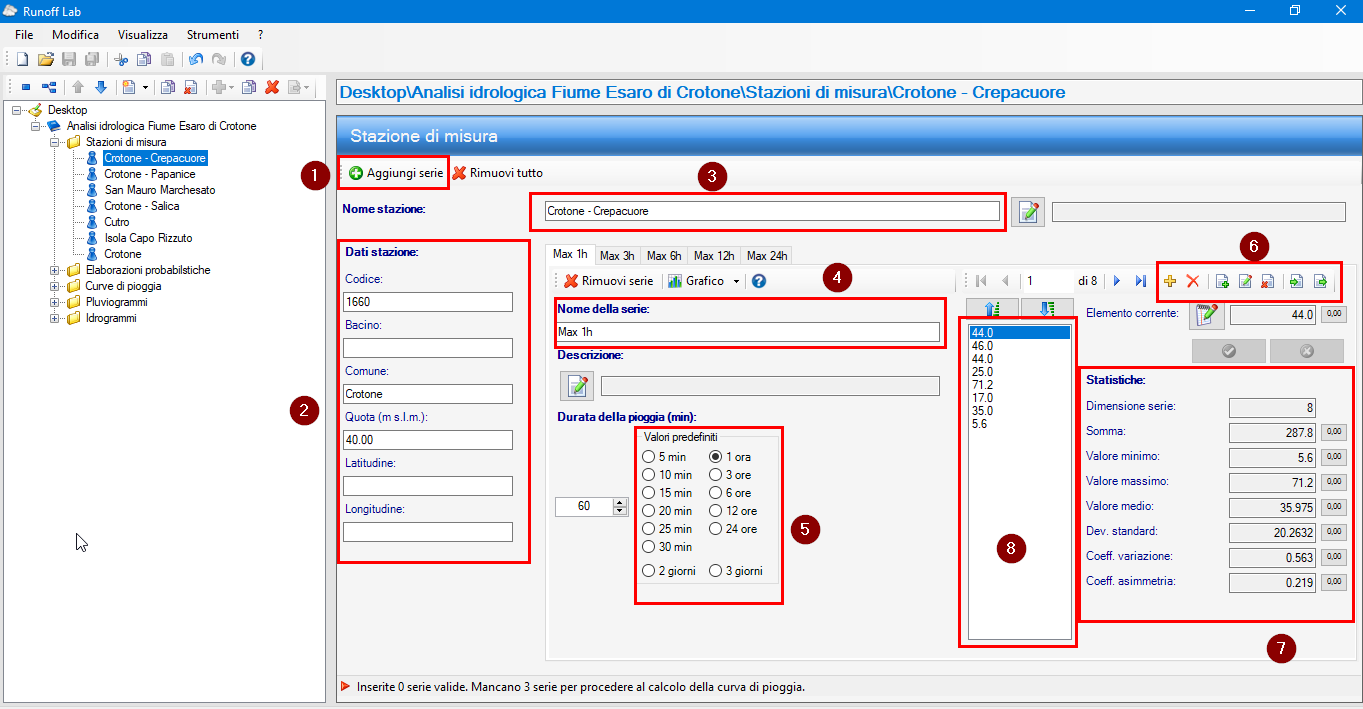
Figura 3 - Interfaccia menù Stazione pluviometrica
Nello specifico:
1.Comando per aggiungere una nuova serie di dati;
2.Dati della stazione pluviometrica;
3.Nome della stazione pluviometrica;
4.Nome della serie storica;
5.Durata della pioggia relativa alla serie corrente;
6.Opzioni di inserimento, modifica ed eliminazione dati della serie. In particolare questi comandi consentono l'inserimento di un Gruppo di dati: comando copia incolla e caricamento da file di testo;
7.Parametri statistici calcolati in tempo reale in funzione dei dati della serie inseriti;
8.Dati pluviometrici.
Il programma offre altre possibilità, ad esempio la visualizzazione del grafico dell'istogramma delle precipitazioni orarie. In Figura 4 si riporta l'istogramma della serie dei massimi annuali di precipitazione di durata 1 ora.
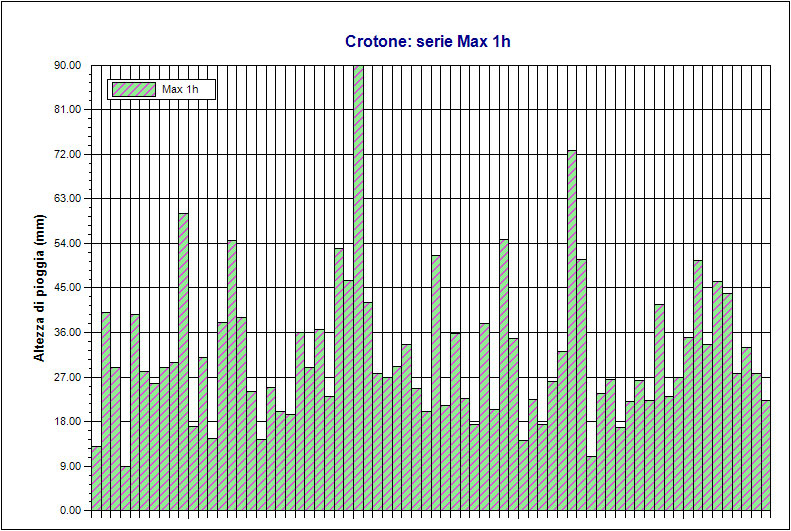
Figura 4 - Istogramma delle piogge Stazione di Crotone
Il grafico è editabile, è possibile modificare: carattere, colori, assi, etichette, font ecc…
Dopo aver inserito i dati della prima stazione, ripetendo i passaggi è possibile inserite tutte le altre.
Elaborazioni probabilistiche
I dati inseriti possono essere trattati statisticamente utilizzando diverse leggi probabilistiche. Occorre selezionare l'opzione “Elaborazioni probabilistiche” e cliccare sul simbolo “+”, in alternativa dal tasto destro del mouse selezionare “Aggiungi elaborazione probabilistica” (Figura 5):
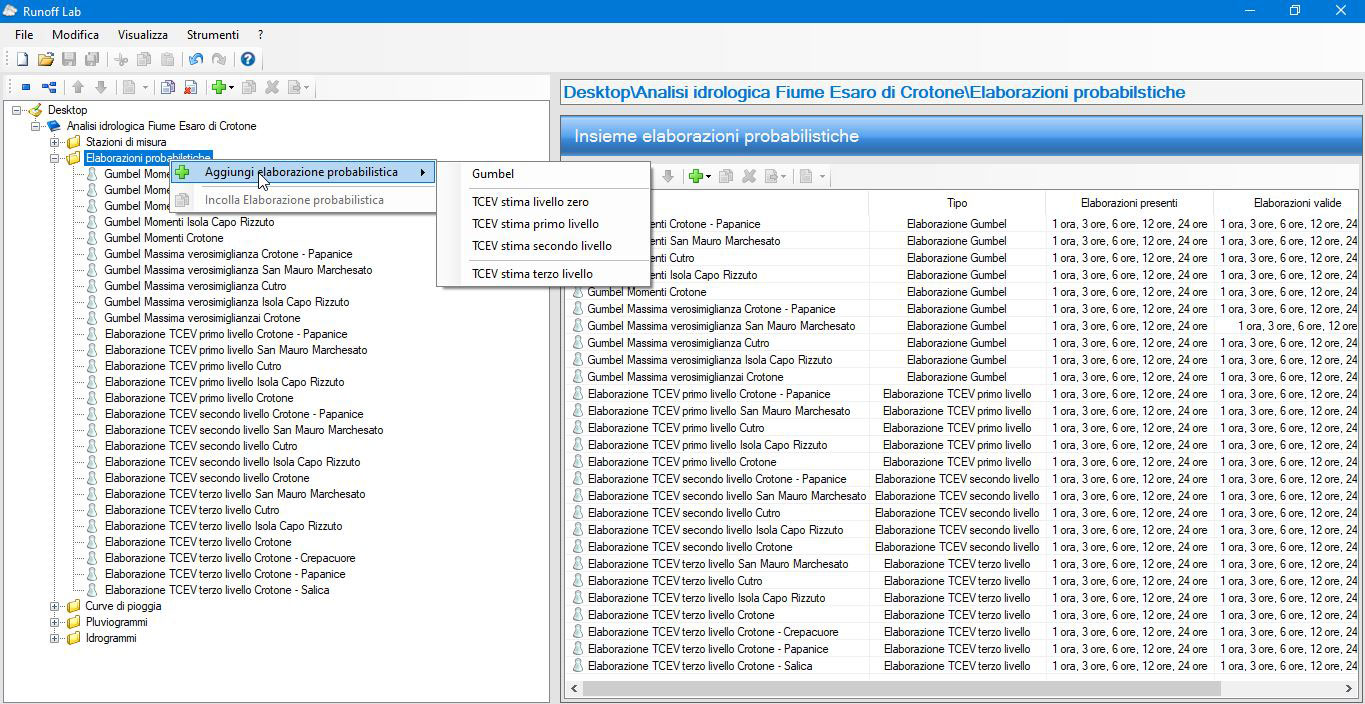
Figura 5 - Aggiunta analisi probabilistica in Runoff Lab
Modello probabilistico di Gumbel o EV1
La funzione di ripartizione (CDF) della distribuzione di Gumbel, o distribuzione del massimo valore del primo tipo, EV1 (Extreme Value Type-1), ha la seguente espressione:
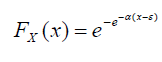
con α>0
Mentre la funzione di densità di probabilità (PDF) assume la forma:
_gumbel.jpg)
I parametri della funzione si possono stimare utilizzando sia il metodo dei momenti, con il quale le stime di ε ed α si ottengono in funzione della media x e dello scarto quadratico medio σx degli n dati del campione a disposizione attraverso le relazioni:
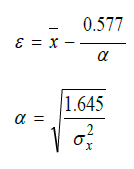
o iterativamente attraverso il metodo della massima verosimiglianza:

Operativamente si procede considerando un valore di primo tentativo α = α1 e lo si sostituisce nel termina a destra della prima espressione, ottenendo, quindi, come soluzione un nuovo valore α̂ = α2. Se |?1−?2| non risulta minore della tolleranza fissata (in GeoStru Elaborazioni idrologiche – Runoff Lab è possibile settare la tolleranza e il numero di iterazioni da Strumenti>Opzioni>Calcolo>Opzioni di Calcolo come si vede in Fig.6), allora si procede al calcolo di un nuovo valore α3 che sia compreso tra α1 e α2.
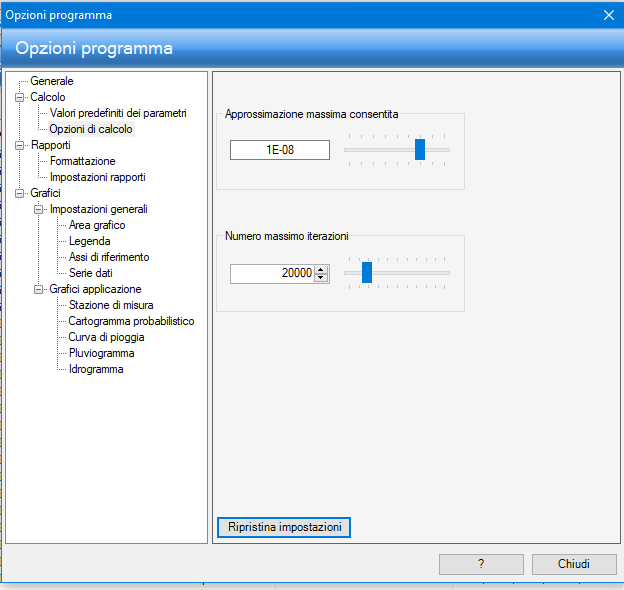
Figura 6 - Opzioni di calcolo in Runoff Lab
Per scegliere il metodo di stima da adottare, dei Momenti o della Massima verosimiglianza, basta selezionarlo sulla finestra di inserimento delle serie pluviometriche , quella di Gumbel è riportata in Figura 7.
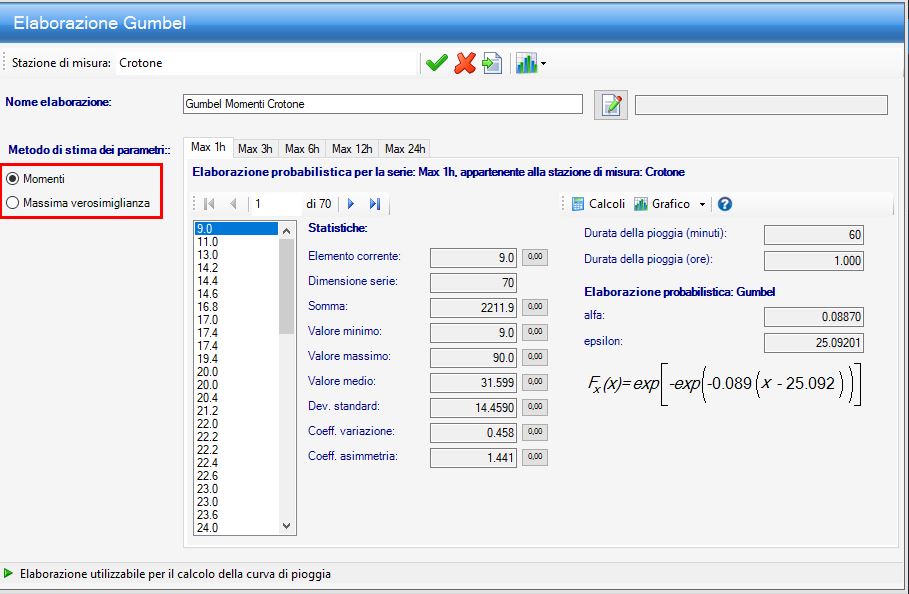
Figura 7 - Impostazione metodo Gumbel in Runoff Lab
Modello probabilistico TCEV
Una migliore interpretazione probabilistica di serie caratterizzate dalla presenza di outliers, si ha con il modello a doppia componente denominato TCEV (acronimo di Two Component Extreme Value), che si rappresenta con una funzione di probabilità cumulata del tipo:
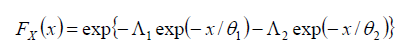
Questa distribuzione, in cui si possono distinguere formalmente una componente base (pedice 1), relativa agli eventi normali e più frequenti, ed una componente straordinaria (pedice 2), relativa ad eventi più gravosi e rari, permette di interpretare fisicamente il processo dei massimi annuali tramite due popolazioni distinte. Tale modello ipotizza che i valori estremi delle piogge non provengano tutti dalla stessa popolazione ma da due diverse popolazioni legate a differenti fenomeni meteorologici. I quattro parametri del modello TCEV hanno un chiaro significato fisico dal momento che Λ1 e Λ2 esprimono il numero medio annuo di eventi superiori ad una soglia delle due componenti, e θ1 e θ2 esprimono il valore medio di tali eventi. L'espressione (5) si può mettere nella forma:
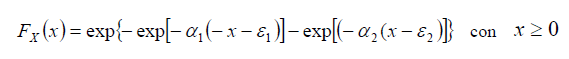
La funzione di probabilità cumulata (5) è esprimibile ancora in altra forma effettuando la trasformazione di variabili θ* =θ2/θ1 e Λ* =Λ2/Λ11/θ*. In questo caso, in modo del tutto equivalente, la (5) si può scrivere:
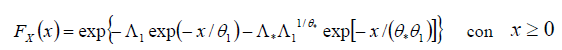
e i quattro parametri che caratterizzano il modello diventano Λ* , θ* , Λ1 e θ1 .
Per la determinazione di xT occorre avere in definitiva una stima dei quattro parametri Λ1, Λ2 ,θ1 e θ2 o equivalentemente dei quattro parametri Λ* , θ*, Λ1 e θ1 , con i quali si può ricostruire integralmente la funzione di probabilità cumulata (5) o (7).
La stima dei quattro parametri si può ottenere ricorrendo al metodo dei momenti o al metodo della massima verosimiglianza, vincolando con quest'ultimo metodo i parametri da stimare alla conoscenza di quelli già noti da indagini a livello regionale.
I parametri della TCEV sono 4 ed è quindi elevata l'incertezza della stima ottenuta con le serie storiche disponibili, la cui dimensione campionaria è in genere inferiore a 80. Per ridurre l'incertezza si utilizzano tecniche d'analisi regionale che consentono di stimare almeno alcuni dei parametri sulla base di tutte le serie storiche ricadenti all'interno di vaste aree indicate come zone e sottozone omogenee.
Al 1° livello di regionalizzazione per i due parametri di forma del modello, θ* e Λ* , si può assumere un valore costante all'interno di ampie zone omogenee. La stima dei valori che tali parametri assumono nella singola zona omogenea risulta pertanto molto affidabile, perché si può ottenere utilizzando tutti i dati delle serie ricadenti all'interno di essa.
Al 2° livello di regionalizzazione, oltre ai valori costanti dei parametri θ* e Λ* nelle zone omogenee, all'interno di queste è possibile identificare sottozone omogenee, entro cui si può ritenere costante anche il parametro di scala Λ1. Anche in questo caso, utilizzando per la stima di Λ1 tutti i dati delle serie ricadenti all'interno della singola sottozona, risulta essere accresciuta l'affidabilità della stima di questo parametro. In totale quindi per questo livello di analisi sono tre i parametri di cui si può assumere a priori un valore regionale.
Al 3° livello di regionalizzazione, oltre ai tre parametri θ* , Λ* e Λ1 di cui si può assumere un valore regionale, identificato al livello precedente, si persegue in modo regionale anche la stima del quarto parametro che sia θ1 o μ in relazione all'approccio che si intende adottare.
Per la TCEV si può dimostrare che:
•il coefficiente di variazione teorico dipende da Λ1, Λ*, θ* ed è indipendente da θ1;
•il coefficiente di asimmetria teorico dipende solo da Λ* e θ* ed è indipendente da Λ1 e θ1.
I coefficienti di asimmetria e di variazione, stimati dalle serie storiche dei massimi idrologici e relativi a più stazioni di misura limitrofe, presentano una limitata variabilità spaziale nell'ambito di vaste aree. Ciò consente di ipotizzare l'esistenza di regioni nelle quali si può ammettere che i valori teorici di tali coefficienti siano costanti e siano quindi costanti i parametri dai quali essi dipendono. Si individuano quindi zone omogenee, nelle quali si possa ammettere costante il coefficiente di asimmetria e quindi i parametri Λ* e θ* ad esso legati, e sottozone omogenee, nelle quali si possa ammettere costante anche il coefficiente di variazione e quindi il parametro Λ1 .
Esistono 4 livelli di regionalizzazione che differiscono fra loro per il numero di parametri stimati in modo puntuale o regionale. La scelta del livello di regionalizzazione al quale fare riferimento dipende sostanzialmente dalla dimensione campionaria.
Per ottenere la funzione di probabilità cumulata della variabile casuale x=ht (massimo annuale della pioggia di durata t) è necessario stimare i parametri Λ*, Λ1, θ*, θ1.
Questa procedura, per brevità, è denominata approccio Fx(x), per cui si ricorre al metodo della massima verosimiglianza, vincolando i parametri da stimare a valori già noti da un' indagine a livello regionale; secondo tale indagine si assume che la Calabria possa essere intesa come una zona pluviometrica omogenea, all'interno della quale è lecito considerare costanti alcuni parametri.
In relazione alle precipitazioni (Tab. 1 e Tab. 2), si è dimostrato infatti che i valori di θ* e Λ* rimangono invariati in tutta la regione, mentre il valore di Λ1 si può supporre costante in ciascuna delle tre sottozone in cui è stata suddivisa la Calabria: jonica, centrale, tirrenica (Fig. 8) .
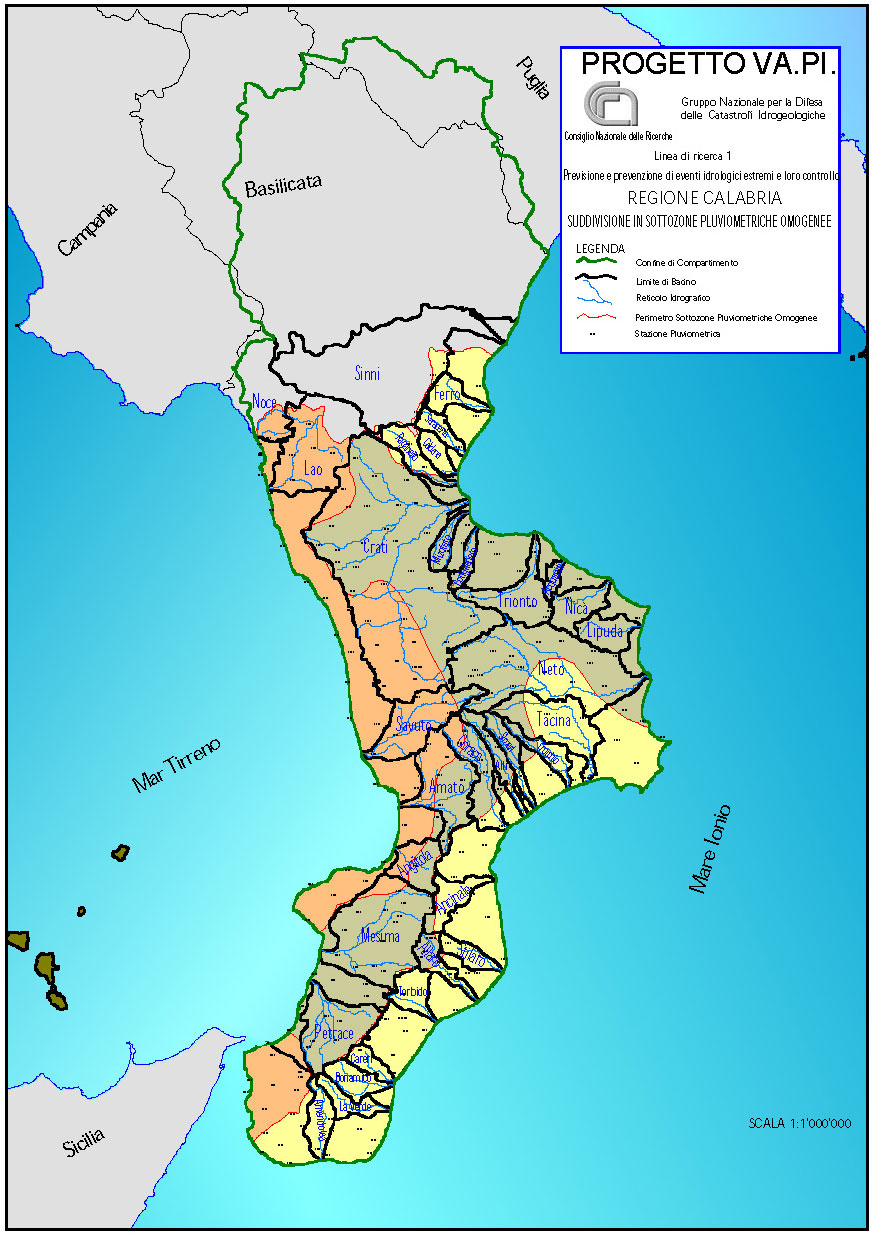
Figura 8 - Suddivisione sottozone pluviometriche omogenee Regione Calabria
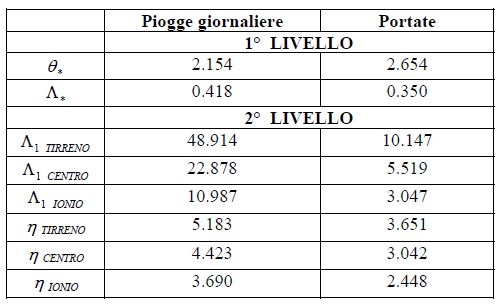
Tabella 1 - Valori Regione Calabria dei parametri TCEV relativi al 1° e al 2° livello per durate giornaliere
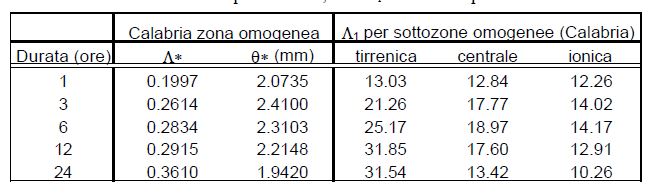
Tabella 2 - Valori Regione Calabria dei parametri TCEV relativi al 1° e al 2° livello per durate orarie
Per scegliere i parametri regionali, occorre accedere al database specifico selezionando il comando![]() evidenziato in Fig. 9 per elaborazioni TCEV di primo livello (Figura 10 e Figura 11) e di secondo livello (Figura 12 e Figura 13):
evidenziato in Fig. 9 per elaborazioni TCEV di primo livello (Figura 10 e Figura 11) e di secondo livello (Figura 12 e Figura 13):
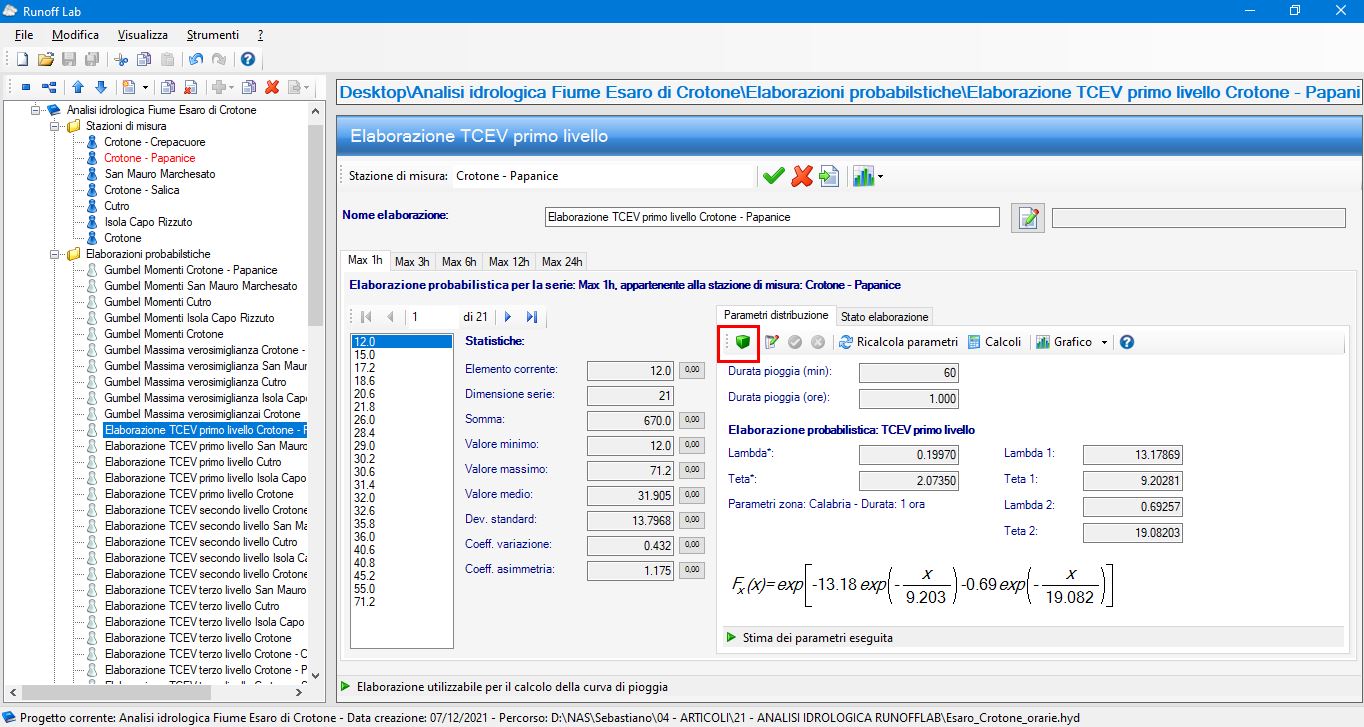
Figura 9 - Impostazione parametri Regionali in GeoStru Runoff Lab
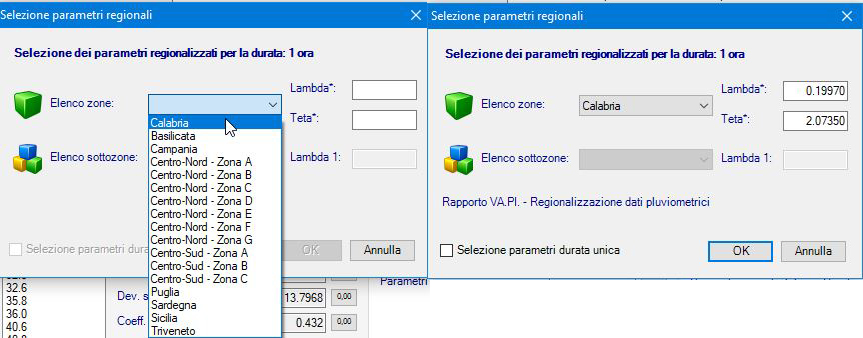
Figura 10 - Valori regionali Calabria parametri piogge orarie TCEV di I livello
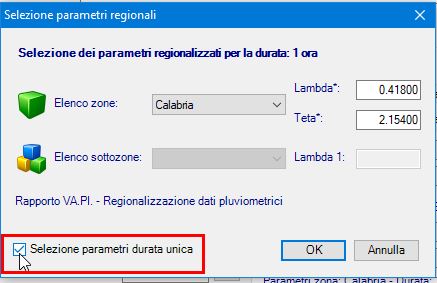
Fig. 11 -Valori regionali Calabria parametri piogge giornaliere TCEV di I livello
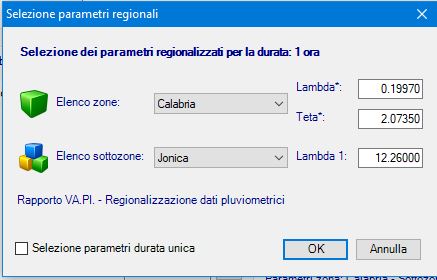
Figura 12 - Valori regionali Calabria parametri piogge orarie TCEV di II livello - sottozona Jonica
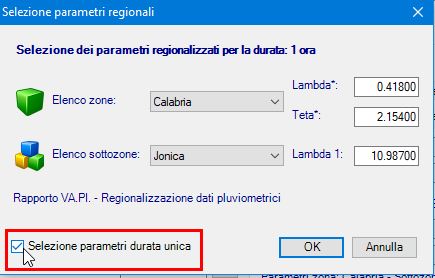
Fig. 13 -Valori regionali Calabria parametri piogge giornaliere TCEV di II livello
Nel caso in cui le osservazioni campionarie manchino completamente o siano scarse per qualità e dimensione, al 3° livello di analisi regionale si preferisce adottare la curva di crescita e affiancare ai valori regionali di Λ*, θ* e Λ1 la stima del valor medio μ ottenuta dalle relazioni empiriche identificate per la singola area omogenea:
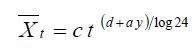
dove y è la quota della stazione rispetto al livello del mare, mentre i parametri a, c e d sono desunti dalla Tabella 3 che suddivide il territorio Regionale in diverse sottozone (Fig. 14):

Tab. 3 - Valori dei parametri al 3° livello delle piogge estreme per singola area omogenea.
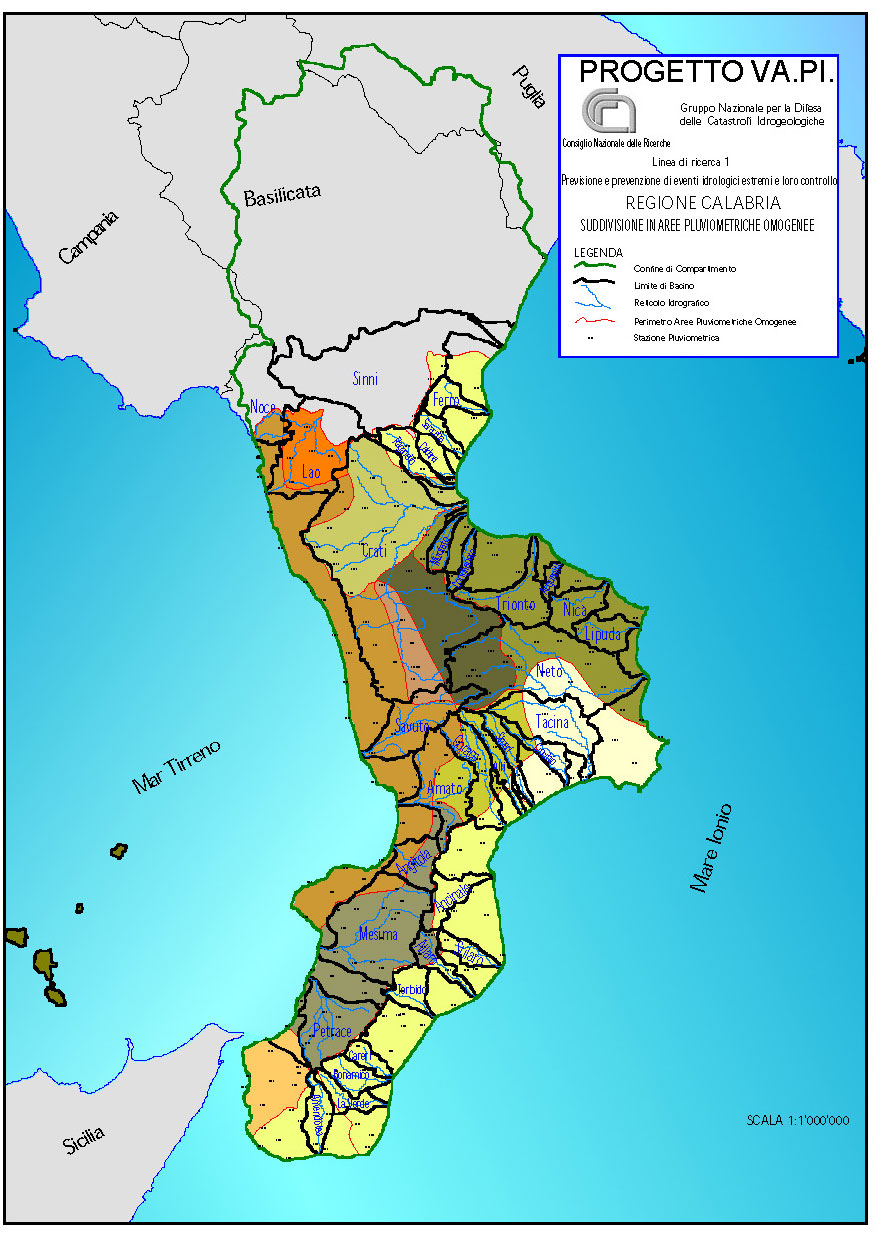
Figura 14 - Suddivisione aree pluviometriche omogenee Regione Calabria
In GeoStru Elaborazioni idrologiche – Runoff Lab, il valore della stima del valore medio è l'unico valore di input richiesto (Fig. 15):
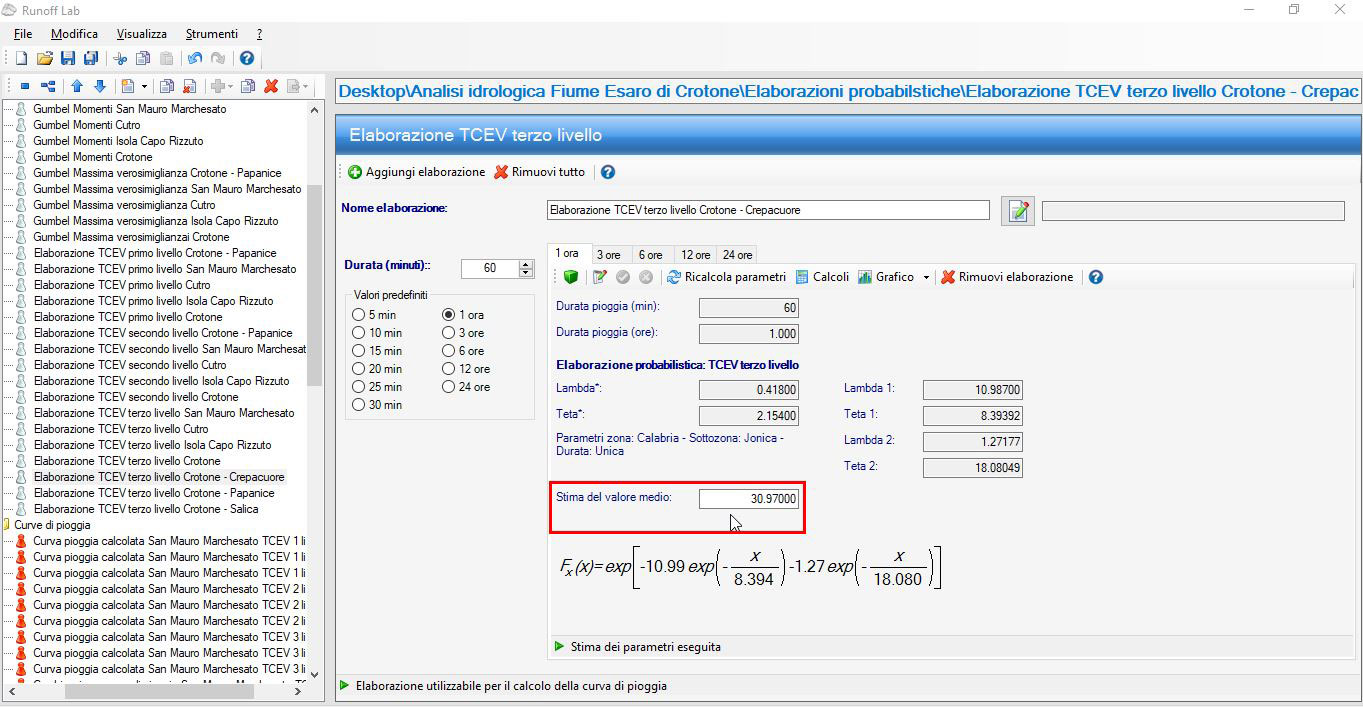
Fig. 15 - Inserimento valore medio in GeoStru Runoff Lab
E' possibile quindi, sulla base della numerosità del campione, eseguire l'analisi considerando diversi livelli di regionalizzazione:
•Livello 0: prevede la stima puntuale di tutti e 4 i parametri. Tuttavia presenta un'elevata incertezza per le dimensioni usuali delle serie campionarie ed è quindi poco utilizzato;
•Livello 1: i parametri θ* e Λ* vengono stimati con elaborazioni su base regionale, mentre Λ1 e θ1 su base campionaria. Questo livello è adottato quando si dispone di almeno 40÷50 anni di osservazione;
•Livello 2: i parametri θ* , Λ*, Λ1 vengono stimati con elaborazioni su base regionale, θ1 su base campionaria. Questo livello è adottato quando i dati a disposizione sono circa 20÷30 anni di osservazione;
•Livello 3: tutti i parametri vengono stimati con elaborazioni su base regionale (è il caso di totale indisponibilità di campioni).
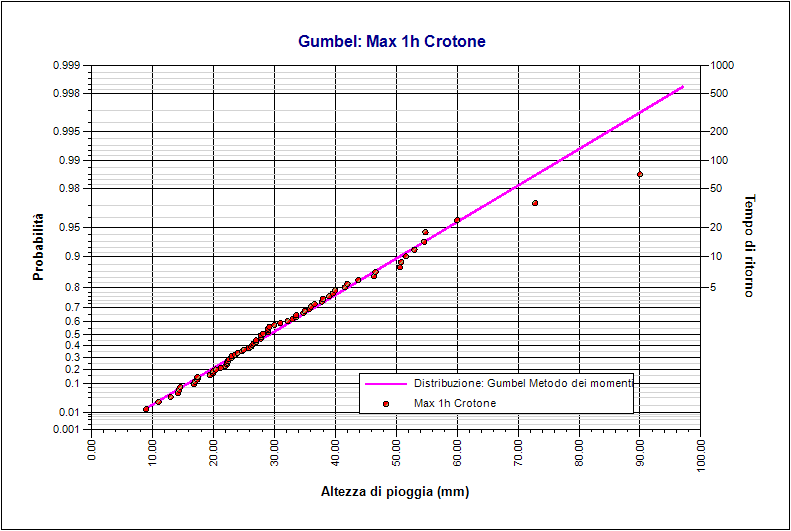
Nel caso in esame, avendo a disposizione dei dati campionari variabili è stato possibile scegliere di effettuare l'analisi al 1° e il 2° livello di regionalizzazione e al 3° livello di regionalizzazione. Sulle seguenti immagini si riportano alcuni dei risultati, su carta probabilistica, delle elaborazioni eseguite in GeoStru Elaborazioni idrologiche – Runoff Lab.
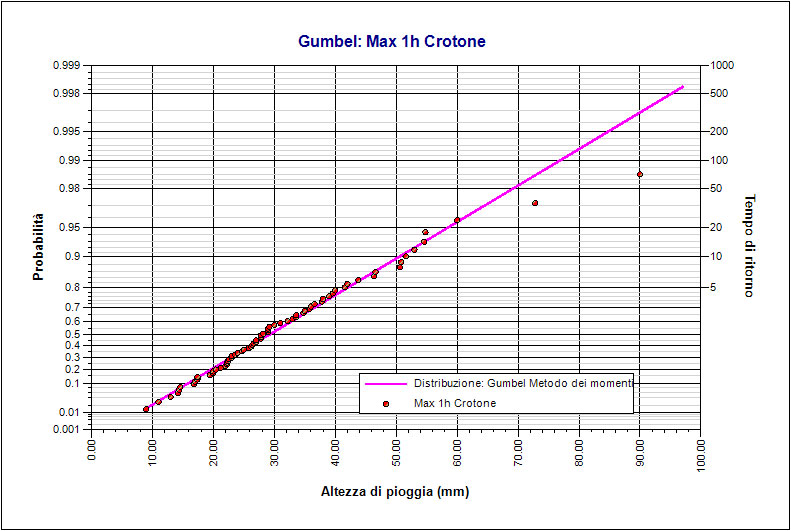

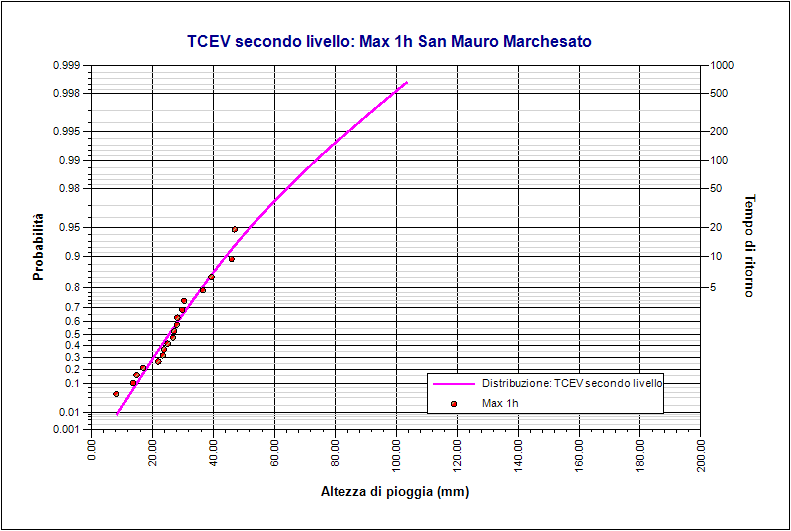

|
© GeoStru