L'insieme dei valori x assunti da una generica grandezza idrologica può essere considerato una variabile casuale X la cui popolazione è costituita dall'insieme di tutti i valori che la x ha assunto per il passato o potrà assumere in futuro.
La serie statistica costituita dagli n valori x1, x2..., xi..., xn assunti dalla x in una determinata stazione di misura, può essere considerato come un campione di dimensione n tratto a caso dalla popolazione della X.
Ci si propone di risalire dalla composizione nota del campione a quella incognita della popolazione, tenendo però bene in conto che, per difetto di campionatura, la composizione del primo può scostarsi, più o meno, da quella della seconda.
All'interno di una generica variabile casuale Z, definita variabile originaria, si considera un campione di dimensione k di osservazioni tratte a caso dalla popolazione della z e si assume come variabile il massimo valore x=zk assunto da z fra le osservazioni del campione.
Posto che dalla popolazione della z possono pensarsi tratti infiniti campioni di dimensione k e posto che zk assume di volta in volta valori diversi, alla distribuzione della variabile originaria z si può associare quella del valore massimo in un campione di dimensione k.
Ciò premesso, la funzione di ripartizione Φ(x) del massimo valore x=zk, raggiunto dalla variabile originaria z in un campione di dimensione k, misura la probabilità che x risulti inferiore o al più eguale a un assegnato valore.
Se fosse nota la funzione di ripartizione Φ(z) della z, Φ(x), in base al quinto assioma del calcolo delle probabilità, sarebbe definito a mezzo della relazione:
![]()
se le k osservazioni che costituiscono il campione sono indipendenti una dall'altra.
In effetti la Φ(z) raramente è nota. Quando però si considerino campioni di grande dimensione, sicché i valori massimi zk risultano spostati nel campo dei valori più grandi della x, ai fini applicativi è sufficiente conoscere l'andamento della Φ(z) in prossimità dei valori massimi e dedurre da questo l'andamento assunto dallaΦ(x) per diversi valori di k, in particolare esaminando se essa tende a una forma asintotica al crescere di k all'infinito.
Nel campo dell'idrologia la Φ(z) risulta generalmente di tipo esponenziale.
Sia ε il valore di z che ci si deve attendere che venga superato una volta su k (estremo atteso), per cui:
![]()
considerando il parametro α=kΦ(z=ε) che misura la rapidità con cui ε varia al variare di k (intensità di funzione) e sviluppando in serie di Taylor la funzione Φ(z) in prossimità di ε si può dimostrare che per grandi valori di z, quale che sia Φ(z), risulta:
![]()
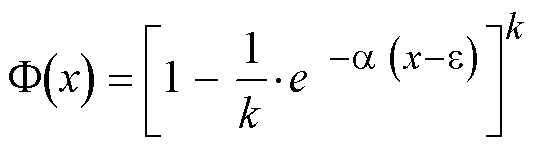
che tende, per k tendente ad infinito, alla funzione asintotica:
![]()
che viene perciò definita legge asintotica del massimo valore, o legge doppio esponenziale o legge di Gumbel.
I parametri ε ed α sono legati alla media η e allo scarto quadratico medio σ della x dalle relazioni:

![]()
|
© GeoStru