For rock slopes, different from those in soil, the Mohr-Coulomb failure criterion can not be used to define the resistance of the material; however with this method is described a procedure that allows the application of the classical methods of Limit Equilibrium even in rocky slopes.
In this purpose are defined the angle of shearing and the cohesion along the sliding surface according to the following expressions:
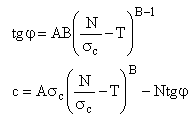
where:
σc is the uniaxial compressive strength of the rock;
A, B, T constants function of the lithotype and the quality of the rock (table below);
N normal stress at the base of the slice.
The constants A, B and T are determined as a function of the classification of the rocks according to Bieniawski (RMR index) or according to Barton (Q index).
Between the two classifications, on the base of 111 examples analyzed, was found the following correlation:
![]()
Lithotype Rock quality |
Limestones Dolomites Marl |
Shales Siltstones
|
Arenites Quartzites |
Andesites Basalts Rhyolites |
Amphibolites Gneiss Granites Gabbros |
|---|---|---|---|---|---|
RMR =100 Q = 500 |
A = 0.816 B = 0.658 T = -0.140 |
A = 0.918 B = 0.677 T = -0.099 |
A = 1.044 B = 0.692 T = -0.067 |
A = 1.086 B = 0.696 T = -0.059 |
A = 1.220 B = 0.705 T = -0.040 |
RMR = 85 Q = 100 |
A = 0.651 B = 0.679 T = -0.028 |
A = 0.739 B = 0.692 T = -0.020 |
A = 0.848 B = 0.702 T = -0.013 |
A = 0.883 B = 0.705 T = -0.012 |
A = 0.998 B = 0.712 T = -0.008 |
RMR = 65 Q = 10 |
A = 0.369 B = 0.669 T = -0.006 |
A = 0.427 B = 0.683 T = -0.004 |
A = 0.501 B = 0.695 T = -0.003 |
A = 0.525 B = 0.698 T = -0.002 |
A = 0.603 B = 0.707 T = -0.002 |
RMR = 44 Q = 1 |
A = 0.198 B = 0.662 T = -0.0007 |
A = 0.234 B = 0.675 T = -0.0005 |
A = 0.280 B = 0.688 T = -0.0003 |
A = 0.295 B = 0.691 T = -0.003 |
A = 0.346 B = 0.700 T = -0.0002 |
RMR = 3 Q = 0.1 |
A = 0.115 B = 0.646 T = -0.0002 |
A = 0.129 B = 0.655 T = -0.0002 |
A = 0.162 B = 0.672 T = -0.0001 |
A = 0.172 B = 0.676 T = -0.0001 |
A = 0.203 B = 0.686 T = -0.0001 |
RMR = 3 Q = 0.01 |
A = 0.042 B = 0.534 T = 0 |
A = 0.050 B = 0.539 T = 0 |
A = 0.061 B = 0.546 T = 0 |
A = 0.065 B = 0.548 T = 0 |
A = 0.078 B = 0.556 T = 0 |
Relation between the classification of the rocks and the parameters A, B and T
© GeoStru