Attention, for the computation of pore water pressure additional data in geotechnical properties must be assigned.
Pore pressure after the earthquake To calculate pore pressures after the earthquake, assign 0 to horizontal and vertical seismic coefficients, and a value different from 0 for the seismic acceleration.
|
Shear strength under seismic loading
In the absence of appropriate experimental determinations, obtained from laboratory cyclic tests, the reduction of shear strength in conditions of seismic loading can be estimated using empirical relations of literature, as indicated in the following paragraphs, with reference to the case of the analysis conducted in terms of effective stress or in terms of total stresses.
Analysis in terms of effective stress
The increase in pore pressure must be assessed in the case of saturated soils if the shearing induced by the seismic action is greater than the value of the volumetric strain, γv.
In partially saturated soils, the pore pressure increases during the application of the seismic activity, but generally is maintained below atmospheric pressure; in this case, can be assumed a zero value of the pore pressure for the entire period of application of the load (σ’=s) and the analysis can be performed using the characteristics of resistance determined in drained tests carried out on specimens of the same material previously saturated. For the calculation of Du should be distinguished the behavior of the soil in relation to their different nature, cohesive or noncohesive.
Cohesive soils
In cohesive soils, the increase in pore pressure Δu, at a certain depth, can be estimated by the following empirical relation (Matsui et al., 1980):
![]()
Where σ’0 is the initial value of the effective average pressure at the considered depth, γc,max is the maximum shearing strain reached during the earthquake and β=0.45 is an experimental coefficient. The volumetric strain γv, determinable with cyclic laboratory tests, can be calculated in first approximation by the relation:
![]()
Where OCR is the over-consolidation ratio, A and B are experimental coefficients that, in the absence of a direct determination, may be derived as a function of the plasticity index; view table below:
Ip (%) |
A |
B |
|---|---|---|
20 |
0.4 10-3 |
0.6 10-3 |
40 |
1.2 10-3 |
1.1 10-3 |
55 |
2.5 10-3 |
1.2 10-3 |
Values suggested for A and B coefficients
The value of γc,max related on the considered depth can be determined by an analysis of the local seismic response. Alternatively, it is determined preliminarily the value of τmax using the empirical relation:
![]()
Where amax, expressed in g, is the peak acceleration at the ground level on the vertical relative to the considered point; g is the gravitational acceleration; σv is the total vertical stress; rd is a reduction factor which takes account of the seismic action at the depth of interest which leads into account the deformability of the subsoil. The factor rd may be calculated, to a first approximation, with the following expression:
![]()
Where z is the depth at the considered point. The maximum shear deformation induced by the earthquake is obtained then by the relation:
![]()
Where the shear modulus G can be determined, using an iteration process, from the curve (G-γ) obtained from laboratory tests.
Granular soils
In granular soils, the increase in pore pressure generated by seismic activity can be estimated by the following empirical relation (Seed & Booker, 1997):
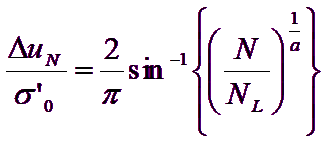
Where ΔuN is the increment of pore pressure after N cycles of load, σ’0 is the initial value of the effective average pressure at the considered depth, N is the number of load cycles of constant amplitude equivalent to the earthquake and NL is the number of load cycles required to produce the liquefaction in the soil. The experimental constant a can be calculated using the relation proposed by Fardis & Veneziano (1981) as a function of the relative density Dr (in fraction):
![]()
The term εq has log-normal distribution with average and unit variance equal to 0.1. To determine the number of cycles N that appears in one of the previous relations it is necessary to approximate the history of irregular shear deformation induced by the earthquake with an equivalent cyclic stress of constant amplitude (τeq) and equivalent number of cycles (Neq) following one of the many procedures described in the literature. For example, using the procedure proposed by Biondi et al. (2004) we obtain:
![]()
![]()
In the first of the above equations τmax is the maximum shear stress induced by the earthquake at a considered depth, whose value can be estimated by an analysis of the local seismic response or, in the first approximation by the relation used in the section on cohesive soils. In the second of the above equations the various terms have the following meaning:
-Ia is the intensity of Arias (m/s);
-v0 is the intensity of the intersections with the time axis of the accelerogram (s-1);
-TD is the duration of the accelerogram defined by Trifunac and Brady (s);
The intensity of Arias is defined by the following formula:
![]()
The other symbols that appear, ie α - β - γ - δ - ε, are constants for which are is recommended the following values:
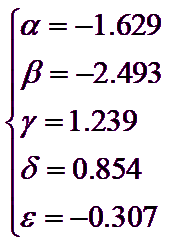
For the determination of the value of NL we can refer to methods that are based on graphic interpolations, or may be used the results of cyclic triaxial tests or cyclic simple shear.
© GeoStru