The limit equilibrium method consists of the study of the equilibrium between a rigid body, such as the slope, and of a slip surface of any shape (straight line, arc of a circle, logarithmic spiral, etc.). From this equilibrium are calculated shear stresses (τ) and compared to the available resistance (τf) calculated according to Mohr-Coulomb's failure criterion. From this comparison we derive the first indication of stability as the Factor of Safety:
F =τf /τ
Among the various equilibrium methods some consider the global equilibrium of the rigid body (Culman), while others divide the rigid body into slices to cater for its non homogeneity and consider the equilibrium of each of these (Fellenius, Bishop, Janbu, etc.).
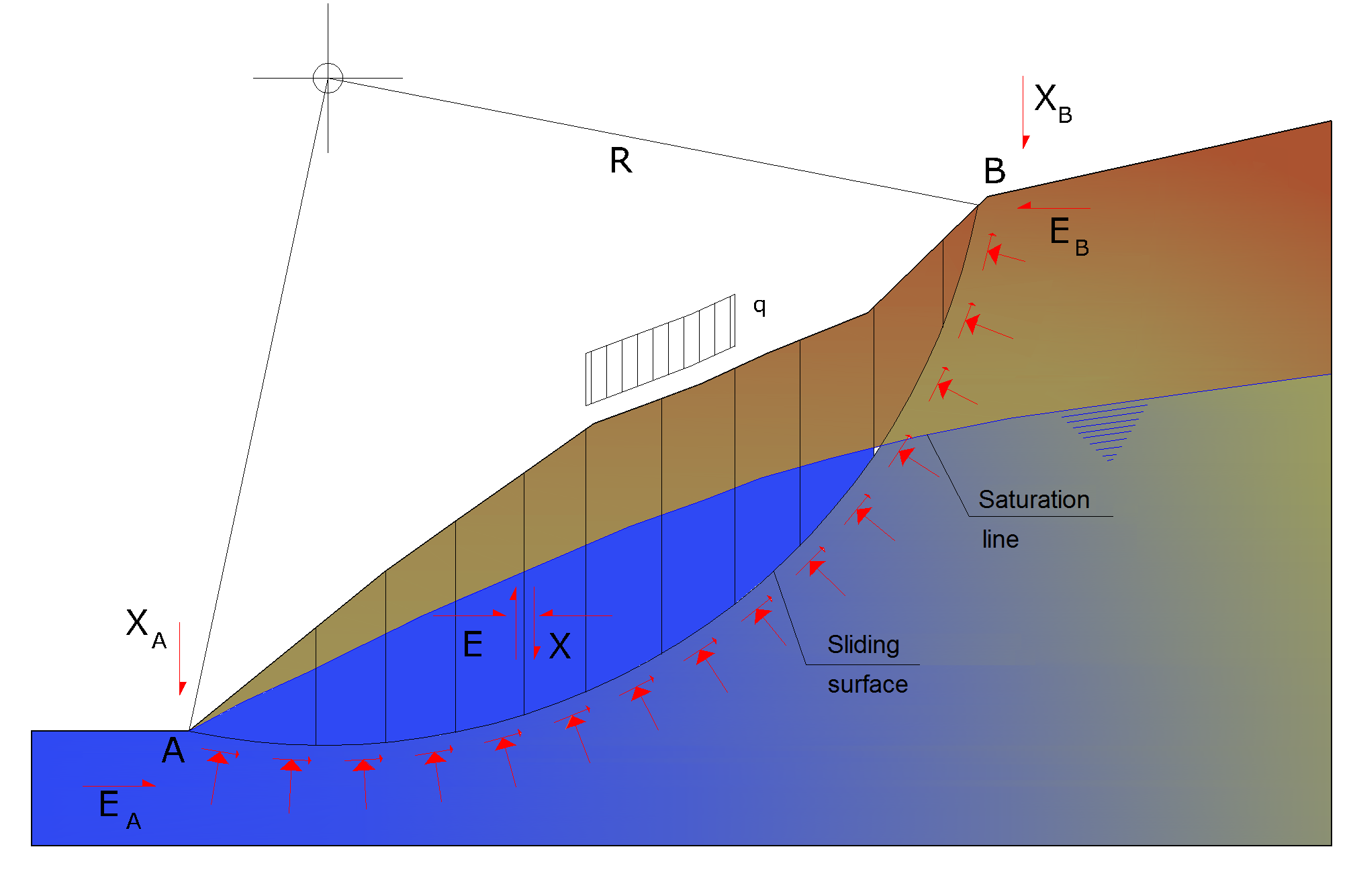
Representation of a calculation section of a slope
Slice method
The volume affected by slide is subdivided into a convenient number of slices. If the number of the slices is n the problem presents the following unknowns:
•n values of normal forces Ni acting on the base of each slice;
•n values of shear forces at the base of slice Ti;
•(n-1) normal forces Ei acting on slice interface;
•(n-1) tangential forces Xi acting on slice interface;
•n values of the coordinate "a" that identifies the point of application of Ei;
•(n-1) values of the coordinate that identifies the point of application of Xi;
•an unknown constituted by the safety factor F.
In all the unknowns are (6n-2).
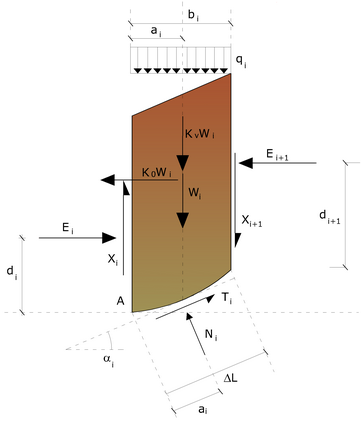
Actions on the i-the slice
While the equations are:
•Equilibrium equations of the moments n;
•Equilibrium equations at the vertical displacement n;
•Equilibrium equations at the horizontal displacement n;
•Equations relative to the failure criterion n.
In all there are 4n equations.
The problem is statistically indeterminate to the extent of:
i = (6n-2)-(4n) = 2n-2
The degree of indetermination is further reduced to (n-2) as it is assumed that Ni is applied at a mid point of the slice, which is equivalent to assume the hypothesis that total normal stresses are distributed uniformly.
The various methods that are based on limit equilibrium theory differ in the way in which the (n-2) degrees of indetermination are eliminated.
© GeoStru