Interfacciamento tra i blocchi
Con questo metodo il terreno viene modellato come una serie di elementi discreti, che in seguito chiameremo "blocchi", e tiene conto della mutua compatibilità tra i blocchi stessi. A questo scopo ogni blocco e i blocchi adiacenti e la base sono vincolate da molle alla Winkler. Vi sono una serie di molle nella direzione normale all'interfaccia per simulare la rigidezza normale e una serie di molle nella direzione tangenziale per simulare la resistenza allo scorrimento dell'interfaccia. Il comportamento delle molle normali e di quelle trasversali, è assunto di tipo elasto-plastico perfetto. Le molle normali non cedono in compressione ma cedono solo a trazione con una capacità estensionale massima per terreno dotato di coesione e senza capacità estensionale per terreni non coesivi.
Le molle trasversali cedono quando è raggiunta la massima resistenza a taglio ed occorre distinguere due tipi di comportamenti diversi: terreno fragile e terreno non fragile. Per terreno fragile la resistenza di picco delle molle a taglio è data da:
![]()
Mentre la resistenza residua
![]()
Per semplicità nella seguente analisi si è assunto che dopo il raggiungimento della resistenza di picco, la resistenza del terreno si abbatte immediatamente al valore della resistenza residua.
Per terreno non fragile la resistenza non si riduce per grandi deformazioni a taglio, quindi la resistenza residua è uguale a quella di picco.
La formulazione del metodo esposto segue quello di una precedente ricerca svolta da Chang e Mistra sulla meccanica dei particolari discreti.
Posti uia, uib, e ωa, ωb in modo che essi rappresentano rispettivamente lo spostamento e la rotazione dei blocchi A e B, si prende il punto P in modo che sia il punto medio dell'interfaccia tra i due blocchi, come mostrato in Fig. 7.1.1. Detto riap il vettore congiungente il baricentro del blocco A con il punto P. Lo spostamento del blocco B relativo al blocco A, nel punto P, è allora espresso come segue:
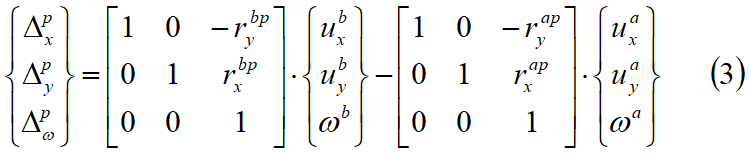
Se il blocco B è comunque immobile, i valori di uxb, uyb, e ωb sono assunti pari a zero.
Prendiamo nip in modo che esso sia il vettore normale sulla faccia del blocco A nel punto P, verso l'interno definito da nip = (cosα , sinα) dove α è l'angolo tra l'asse X e il vettore nip . Il vettore sip, perpendicolare al vettore nip, sarà definito da sip = (-sinα, cosα).
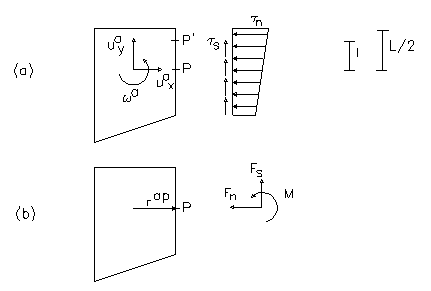
Figura 7.1.1- (a) tensioni normali e tangenziali ; (b) forze e momenti equivalenti all'interfaccia.
ll vettore spostamento del primo membro dell'Eq. 3 può essere trasformato dalle coordinate X-Y nelle coordinate locali n-s come segue:
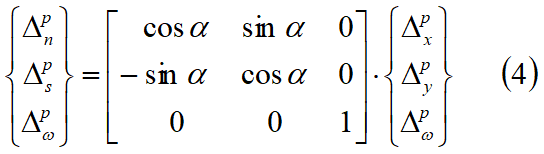
A causa dello spostamento relativo tra due blocchi vicini, per un generico punto P' dell'interfaccia, distante l dal punto centrale P come evidenziato nella Fig.7.1.1, l'allungamento della molla nella direzione normale dn e quello nella direzione tangenziale ds sono date da:
![]()
Per effetto dell'allungamento delle molle insorgono tensioni normali e tangenziali in accordo con il comportamento alla Winkler, come mostrato in Fig. 7.1.1. Tali tensioni sull'interfaccia possono essere integrate per ottenere forze e momenti risultanti equivalenti nel modo seguente:
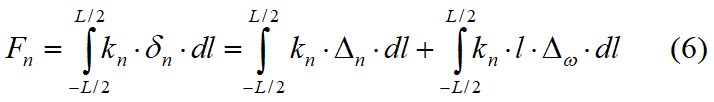
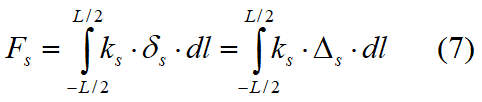
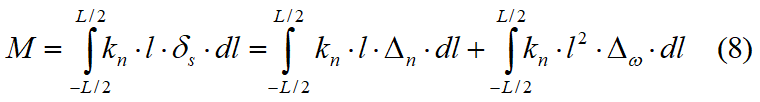
dove
kn = costante della molla normale per unità di lunghezza
ks = costante della molla trasversale per unità di lunghezza
L = lunghezza dell'interfaccia
Occorre notare che le molle sono di tipo elasto-plastico quindi i valori di kn e ks sono funzione della deformazione, quindi dovrebbero essere ottenute dalle curve sforzi -deformazioni rappresentate in Fig. 7.1.2. Per le interfaccie che non cedono, vengono usate le costanti elastiche kn e ks . Per quelle che cedono le costanti elastiche non possono essere utilizzate, quindi è richiesto un metodo per considerare la non linearità del problema. A tal proposito viene impiegato il metodo della rigidezza secante. Le costanti equivalenti ` kn e ` ks possono essere ottenute come quelle corrispondenti alla deformazione dell'interfaccia, come evidenziato in Fig. 7.1.2.
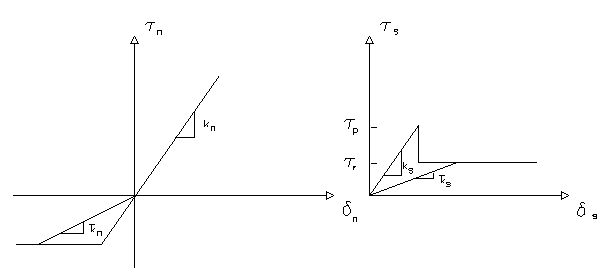
Figura 7.1.2- Rappresentazione del metodo della rigidezza secante, definizione delle costanti equivalenti 'Kn, 'Ks
Integrando tali espressioni, dato che i termini che includono il primo ordine Kn·L sono nulli si ottiene:
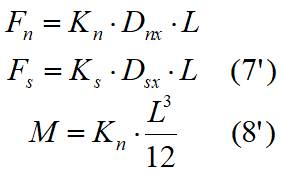
ossia, in forma matriciale:
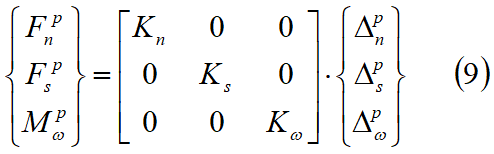
dove:
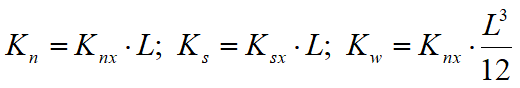
Per convenienza, trasformiamo le forza di interfaccia FnP e FsP in FxP e FyP , passando rispettivamente dal sistema di coordinate locali n-s al sistema globale X-Y nel seguente modo:
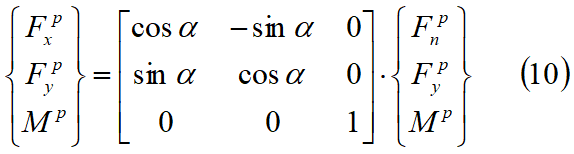
Le forze risultanti agenti su ogni faccia di un blocco devono soddisfare le condizioni di equilibrio date da:
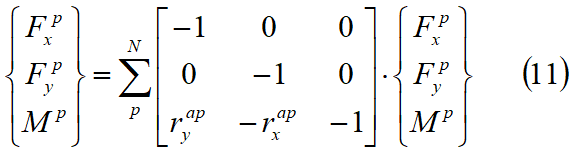
dove N è il numero totale di facce del blocco. Le variabili fxa, fya, ma sono le forze ed i momenti di massa gravitazionali del blocco A. Combinano le equazioni 3, 4, 9, 10 e 11 otteniamo un legame tra forze e spostamenti del blocco A come di seguito riportato:
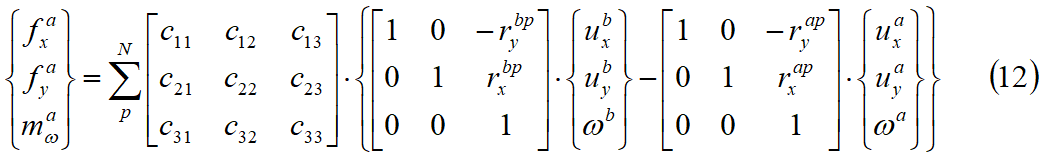
la matrice [c] è data dal prodotto delle seguenti matrici:
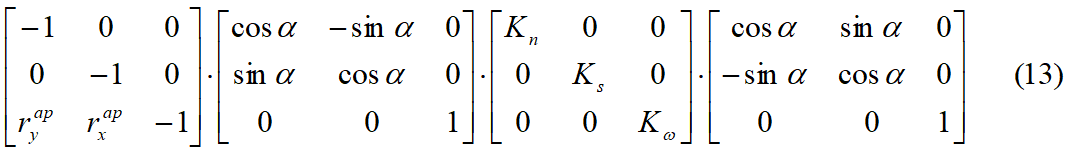
Facendo riferimento all' Eq. 12, per ogni blocco possiamo scrivere le tre equazioni di equilibrio delle forze e dei momenti, ottenendo un sistema di 3× N equazioni, per N blocchi, è espresso nel modo seguente:
![]()
{ f } : è composta da fx, fy e m, per ogni blocco
{ u } : è composta da ux, uy ed ω, per ogni blocco
[G]: è la matrice di rigidezza totale.
Quindi per ogni blocco abbiamo sei variabili le forze di massa fx, fy e m ed gli spostamenti ux, uy e la rotazione ω, delle quali tre sono note cioè : fx ed m sono, uguali a zero.
Risolvendo il sistema delle 3×N equazioni si ricavano le 3×N incognite.
Trovati gli spostamenti baricentrici di ogni blocco, tramite l'equazione 3 si possono ricavare gli allungamenti delle molle tra due blocchi adiacenti. Da questi allungamenti tramite le relazioni forze-allungamenti (Eq. 4 e 9), si possono ricavare le forze normali e tangenziali. Infine si possono ricavare le tensioni normali σn e tangenziali τs agenti su ogni interfaccia di due blocchi, dividendo le forze trovate per l'area dell'interfaccia stessa, ossia:
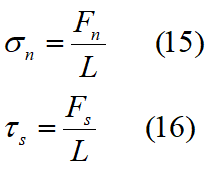
© GeoStru