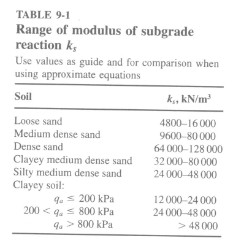
It is possible (in the context of analysis with the finite element method) to manage the stiffness of the springs which schematize the soil. The environment for the management of the stiffness modules is the following:
•Node: It is the node (within the finite element discretization) upon which to impose the assigned stiffness.
•Depth: It is the depth at which the node is positioned, or possibly the depth at which you want to fix the modulus of subgrade reaction.
•Computation method: It is the calculation method through which the modulus of subgrade reaction must be determined. The software allows choosing from the following options:
User
The user can select different soils, from the drop-down text box, each being associated to a range of values for the modulus of subgrade reaction. The user can enter a numerical value for the modulus of subgrade reaction and click the double blue arrow in order to assign the entered value.
Bearing capacity
According to the method which exploits the concepts of bearing capacity, the modulus of subgrade reaction is calculated on the basis of the following formula:
![]()
The user must enter the parameters As, Bs and n so as to allow the software to calculate the modulus of subgrade reaction applying the formula.
"The most general form of either a horizontal or a lateral modulus of subgrade reaction is:
Ks = As + BsZn (9-10)
where: As = constant for either horizontal or vertical numbers
Bs = coefficient of depth variation
Z = depth of interest below ground
n = exponent to give ks the best fit (if load test or other data are available)
Either As or Bs in this equation may be zero; at ground surface As is zero for a lateral ks but at any small depth As > 0. For footings and mats (plates in general), As > 0 and Bs @ 0. Equation (9-10) can be used with the proper interpretation to the bearing-capacity equations of Table 4-1 (with di factor dropped) to give
qult = c×Nc×sc + γ×Z×Nq×sq +0.5×γ×B×Nγ×sγ (9-10a)
Observing that
As = C×(c×Nc×Sc + 0.5×γ×B×Nγ×sγ) and Bs×Z1 = C×(γ×Nq×sq)Z1
We obtain a ready means to estimate ks. In these equations the Terzaghi or Hansen bearing-capacity factors can be used. The C factor is 40 for SI units and 12 for Fps, using the same reasoning that qult occurs at a 0.0254-m and 1-in. settlement but with no SF, since this equation directly gives qult. Where there is concern that ks does not increase without boundwith depth Z, we may adjust the BsZ term by one of two simple methods:
Method 1: Bs×tan-1 (Z/D)
Method 2: (Bs/Dn)×Zn = B’s×Zn
where
D = maximum depth of interest, say, the length of a pile
Z = current depth of interest
N = your best estimate of the exponent
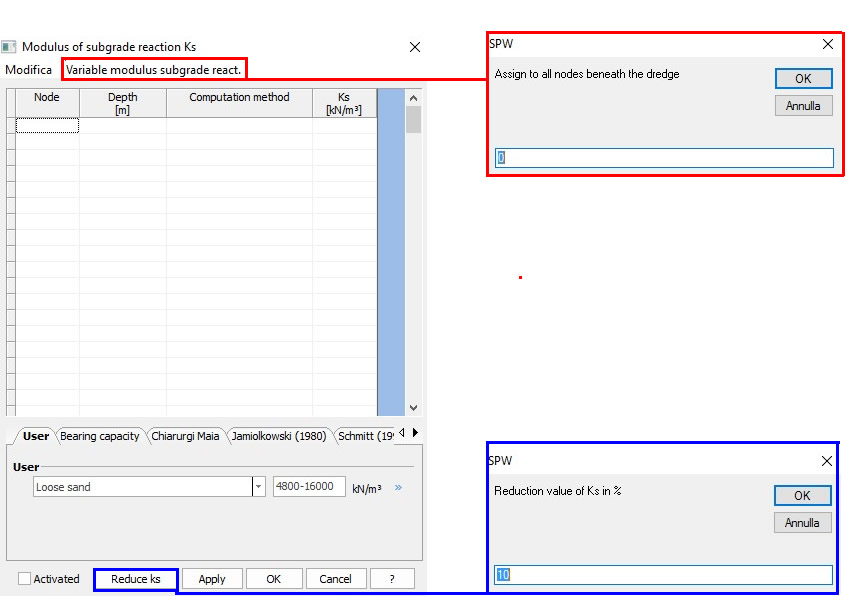
Table 9-1 may be used to estimate a value of ks to determine the correct order of magnitude of the subgrade modulus obtained using one of the approximations given here. Obviously if a computed value is two or three time larger that the table ranger indicates, the computations should be rechecked for a possible gross error. Note, however, if you use a reduced value of displacement (say, 6 mm or 12 mm) instead of 0.0254 m you may well exceed the table range. Other than this, if no computational error (or a poor assumption) is found then use judgment in what value to use. The table values are intended as guides. The reader should not use, say, an average of the range given as a “good” estimate. "
Joseph E. Bowles (1997), "Foundation analysis and design"
|
Joseph E. Bowles (1997), "Foundation analysis and design" |
Chiarurgi-Maia method
This method is used to calculate the modulus of subgrade reaction on the basis of the oedometric modulus, of the diameter of the piling and of Poisson’s ratio. The formula applied to calculate the modulus of subgrade reaction using this method is the following:
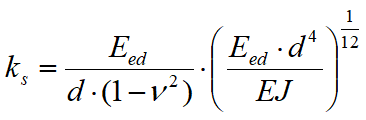
In the previous formula, Eed is the soil oedometric modulus, d is the diameter of the pile, n is Poisson’s ratio ad EJ is the flexural stiffness of the piling.
Jamiolkowski’s method
This method is used to calculate the modulus of subgrade reaction on the basis of the following parameters:
•secant modulus of elasticity, expressed in kPa
•dimensionless coefficient which depends on the bound model assumed for the calculation of the bulkhead (it is equal to 1 for free bulkheads)
•dimensionless coefficient which depends on the depth at which to calculate the modulus of subgrade reaction
•bulkhead embedment depth, expressed in m
In particular, Jamiolkowski’s method refers to the secant modulus of elasticity of the ground corresponding to the activation of 50% of the limit pressure (Es,50). Therefore, for the calculation of the modulus of subgrade reaction, the following formula is applied:
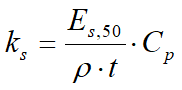
In the previous formula, t is equal to the embedment depth and r is a dimensionless coefficient equal to 1 for free diaphragm on the foot or to the ratio of the position of the null displacement point beneath the dredge line to the embedment depth for the diaphragm with partial fixed joint on the foot. Cp is a dimensionless depth coefficient estimated using the following formula:
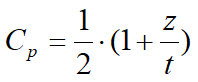
Schmitt’s method
This method is used to calculate the modulus of subgrade reaction on the basis of the diameter of the section, of the modulus of elasticity of the ground and of the modulus of elasticity of the material constituting the structure. In particular, Schmitt proposes to refer to the oedometric modulus of the ground Eed as well as to the stiffness relevant to the supporting structure (expressed through the characteristic length λ of the Winkler beams), obtaining:
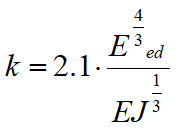
where Eed is the edometric modulus of the ground, while EJ represents the flexural stiffness of the bulkhead.
Ménard’s method
This method is used to calculate the modulus of subgrade reaction of the ground on the basis of the results of tests carried out using the Ménard pressuremeter. In particular, the modulus of subgrade reaction is estimated on the basis of the following factors:
oEM, pressurmeter modulus, expressed in kN/m2
ocoefficient which takes into account the viscous behaviour (dimensionless coefficient)
ocharacteristic length, expressed in m
In particular, this method refers to the pressuremeter modulus of the ground EM, obtained experimentally through a pressuremetric test:
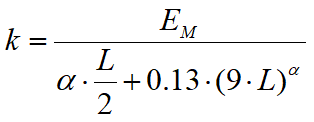
Where a is α coefficient which takes into account the viscous behaviour of the ground, and L is a characteristic length that the author indicates as corresponding to 2/3 of the bulkhead embedment depth.
The Reduce ks button activates a dialog box where must be entered the percentage value of which is to reduce the subgrade reaction module.
It is possible to automatically assign a value to the modulus of subgrade reaction for all the nodes under the bottom of the excavation line by selecting Variable modulus of subgrade react. / Assign to all nodes beneath the dredge.
Click Apply for the software to take into consideration all data entered in this window.
© GeoStru