En el SPW se puede tener en cuenta la presencia de posibles cargas repartidas sobre el relleno en términos de Líneas, Franjas o Cargas Uniformes. El ambiente de administración de los tipos de carga es el siguiente:
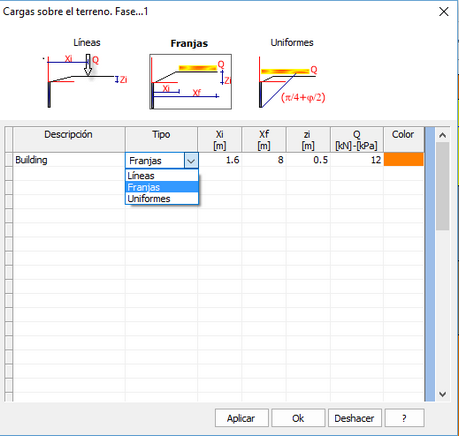
Ambiente de administración de las cargas repartidas
Los datos a insertar para definir correctamente una carga son los siguientes:
•Descripción: Identifica la carga. Este dato es necesario para reconocer la acción en las combinaciones de carga.
•Tipo: Se puede elegir entre líneas de carga, franjas de carga, o cargas uniformemente repartidas.
•xi: Es la abscisa a partir de la cual la carga comienza a actuar. En caso de líneas de carga, es la abscisa que define la aplicación de la línea de carga. Se expresa en m.
•xf: Se requiere este dato cuando se definen franjas de carga o cargas uniformes. Es la abscisa final de la carga (por lo tanto establece la extensión de la carga). Se expresa en m.
•zi: Profundidad expresada en m. Su validez es solo gráfica, por lo tanto el incremento de tensión provocado por la sobrecarga se determina a partir de la coronación de la pantalla.
•Q: Intensidad de la carga, expresada en kN (si se trata de línea de carga) o en kN/m² si se trata de de carga y de carga uniforme.
•Color: Se asigna el color con el que se verá la franja de carga.
Nota: Las cargas se distribuyen por metro lineal en dirección longitudinal.
La siguiente figura es útil para interpretar los diferentes tipos de cargas:
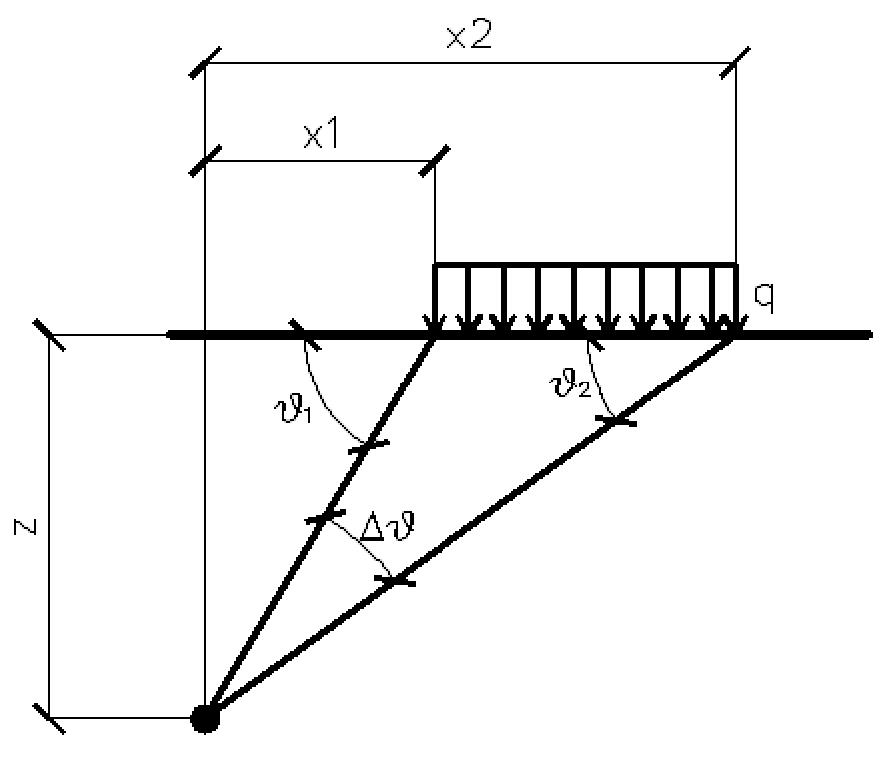
Franjas de carga ortogonales
Con las Franjas de carga se estima la distribución de las tensiones en función de la profundidad z.
Una carga repartida en modo parcial con abscisa inicial x1 y abscisa final x2 genera un diagrama de presiones en la pared cuyos valores se determinan según la fórmula de TERZAGHI, que exprime la presión en la profundidad genérica z como a continuación:
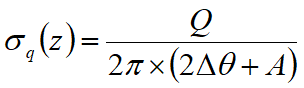
Δϑ = ϑ1-ϑ2;
A = sen(2ϑ1)-sen(2ϑ2)
B = cos(2ϑ1)-cos(2ϑ2)
ϑ1 = arctg(z/x1)
ϑ2 = arctg(z/x2)
Por integración se obtiene el resultado y el relativo brazo.
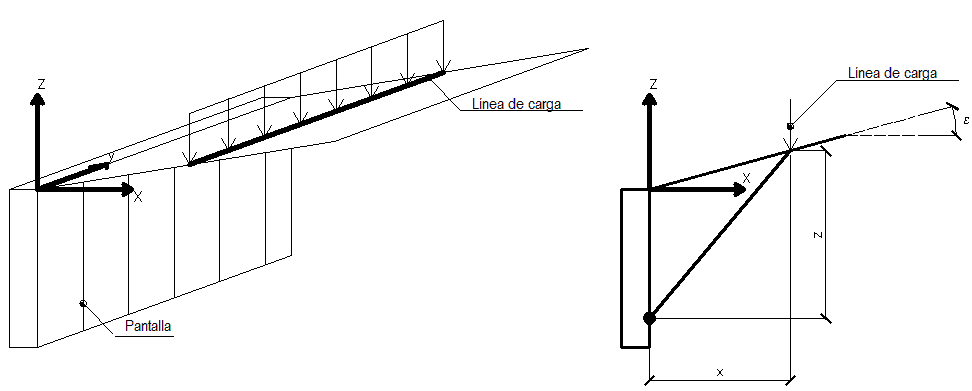
Esquema de las líneas de carga
Con las líneas de carga, como con las franjas de carga, se estima la distribución de las tensiones en función de la profundidad z. Las líneas de carga generan un incremento de presiones en la pared que según BOUSSINESQ, en la profundidad z, se pueden expresar como a continuación:
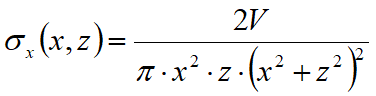
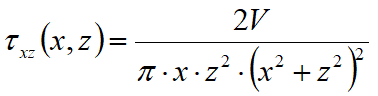
Donde los símbolos tienen el siguiente significado:
V = Intensidad de la carga expresada en [F/L];
X = Distancia, en proyección horizontal, del punto de aplicación de la carga de la pared
Si el plano de acción tiene una inclinación de ε, el sistema de referencia cambia de (x,z) a (X,Z), por medio de la siguiente transformación:
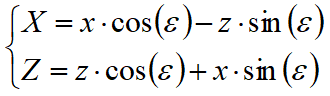
Una carga Q, uniformemente repartida en el plano del terreno provoca presiones constantes iguales a:
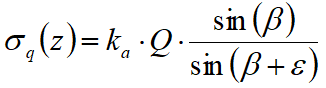
Integrando la tensión en la fórmula precedente se obtiene el empuje total debido a la sobrecarga:
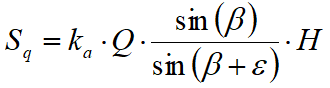
Con punto de aplicación en H/2 (la distribución de las tensiones es constante). Los símbolos de las fórmulas anteriores tienen los siguientes significados:
β = Inclinación de la pared interna con respecto al plano horizontal pasante por el pie
ε = Inclinación del plano del terreno con respecto al plano horizontal. Positiva si va en dirección contraria a las manecillas dl reloj.
Ka = Coeficiente de presión activa calculado en el párrafo anterior.
Nota: La carga uniforme se distribuye automáticamente desde la coronación de la pantalla, en toda la amplitud de la cuña de rotura.
© Geostru