<< Click to Display Table of Contents >> Navigation:  SPW Pantallas > Informe... > Ejemplo relación de cálculo

RELACIÓN DE CÁLCULO

 

Introducción

Las pantallas son obras de ingeniería civil usadas para resolver problemas relacionados con la estabilidad de taludes o con la contención de terraplenes.  No obstante, se emplean también en las obras portuarias para el atraque de embarcaciones, en las excavaciones para apuntalar las paredes, o en trabajos subacuáticos para realizar obras estancas. Por lo tanto, es posible intuir la importancia que se debe dar al  diseño de tales obras, especialmente a todo lo que tiene que ver con el proyecto estructural y geotécnico.

En cuanto al cálculo, vale la pena señalar que hasta la fecha no existen métodos exactos y esto es debido a la interacción tan compleja que existe entre la profundidad de excavación, la rigidez del material de la pantalla y la resistencia debida a la presión pasiva. En todo caso, los métodos comúnmente utilizados se pueden clasificar en dos categorías:

1.Métodos basados en la discretización del modelo de pantalla (diferencias finitas o di elementos finitos).

2.Métodos hipotéticos, cuya finalidad es afrontar el problema estudiando el equilibrio de un cuerpo rígido.

Entre estas dos categorías, el método de los elementos finitos resulta ser el más racional, ya que se basa en consideraciones que implican tanto la estática del problema (equilibrio) como la cinemática (congruencia).

 

Tipos de pantallas.

Los tipos de pantalla más utilizados actualmente se pueden clasificar de la siguiente manera:

3.Pantallas en hormigón armado, de pilotes o continuas

4.Pantallas de madera

5.Pantallas de acero

 

Análisis de la pantalla

 

Algunas consideraciones preliminares.

Son varios los elementos a considerar para el cálculo de una pantalla. De hecho, son elementos concernientes a la flexibilidad de los pilotes, al cálculo del empuje del relleno, a la rigidez del terreno, etc.

Figura 1: Esquema de las presiones agentes en la pantalla

 

Como se muestra en la figura anterior, las presiones laterales que participan en el equilibrio son la presión activa que se produce detrás de la pantalla (en el trasdós) y la presión pasiva que se produce en la parte delantera de la pantalla (intradós). El cálculo, ya sea con métodos simplificados que con métodos numéricos, del empuje en el trasdós y en el intradós generalmente se efectúa con el método de Rankine y/o con el de Coulomb. Se observa sin embargo que el método de Coulomb proporciona resultados más precisos visto que, siendo la pantalla una obra por lo general a flexión y por lo tanto con mayores corrimientos, se generan fenómenos de rozamiento en la interfaz pantalla-terreno que solo se pueden tener en cuenta con los coeficientes de empuje de Coulomb.

Con el método de los elementos finitos se debe calcular el coeficiente de balasto, junto con el empuje activo y pasivo del terreno. Si se trata de análisis en condiciones no drenadas, se debe además conocer el valor de la cohesión no drenada. También es importante considerar que si se desea tomar en cuenta el rozamiento terreno-obra, entonces es necesario saber el respectivo ángulo de rozamiento. En resumen, los parámetros (en términos de propiedades del terreno) necesarios para el análisis son los siguientes:

1.Ángulo de rozamiento interno del terreno

2.Cohesión del terreno

3.Peso específico del terreno;

4.Ángulo de rozamiento entre el terreno y el material de la obra.

 

Cálculo de los empujes

Como se ha indicado anteriormente, en todos los casos se debe calcular el empuje activo y pasivo. Por lo tanto en esta sección se expone el cálculo de los empujes con el método de Coulomb.

 

Cálculo del empuje activo

El empuje activo se puede calcular con el método de Coulomb o alternativamente utilizando la Teoría de Caquot.

 

Método de Coulomb

El método de Coulomb toma en cuenta las variables más importantes, sobre todo las que tienen que ver con el fenómeno de rozamiento pantalla-terreno. Con suelo homogéneo y seco el diagrama de las presiones es lineal con distribución (calculada a profundidad z):

El empuje total, que es la integral de la relación precedente en toda la altura, se aplica a 1/3 de H y se calcula con la siguiente expresión:

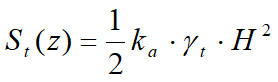
Indicando con ka el valor del coeficiente de presión activa, se determina con la siguiente relación:

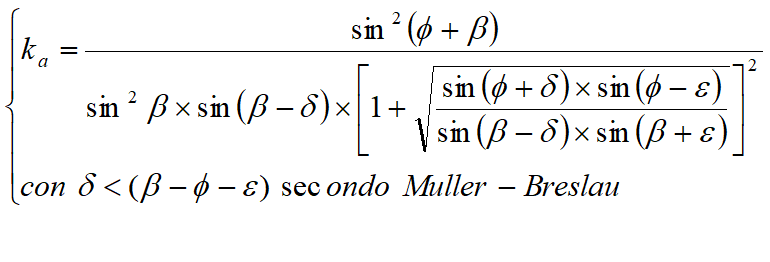
gt        = Peso específico del terreno;

b        = Inclinación de la pared interna con respecto al plano horizontal pasante por la base

f        = Ángulo de resistencia al corte del terreno;

d        =  Ángulo de rozamiento terreno-pantalla positivo si es en el sentido de las manecillas del reloj

e        = Inclinación del plano del terreno con respecto al plano horizontal positiva si es al contrario de las manecillas del reloj

Metodo di Caquot.

El método de Coulomb es bastante preciso al calcular los coeficientes de presiones al estado límite, aunque se basa en la suposición de una superficie de deslizamiento plana. Esta hipótesis se puede superar aplicando la teoría de Caquot, la cual se basa en la utilización de una superficie de deslizamiento de forma espiral logarítmica. Según esta teoría, el coeficiente de presión activa se determina con la siguiente fórmula:

 

Donde:

KaCoulomb es el coeficiente de presión activa calculado con la teoría de Coulomb

r es un coeficiente multiplicativo calculado con la siguiente fórmula:

 

 

Donde:

 

 

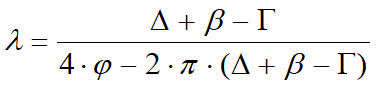
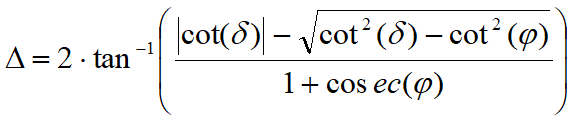
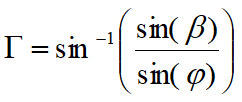
Donde (véase también la figura siguiente):

-b es la inclinación del perfil del trasdós medida con respecto a la horizontal

-f es el ángulo de rozamiento interno del terreno que empuja

-d es el ángulo de rozamiento obra-terreno

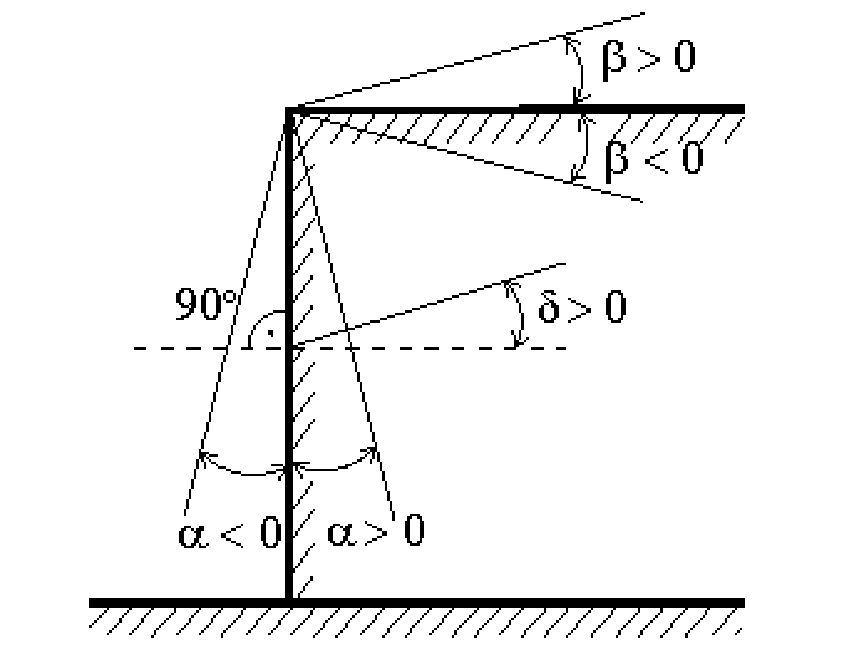
Figura: Convención utilizada en el cálculo del coeficiente de presión según la teoría de  Caquot

Carga uniforme sobre el relleno

Una carga Q, uniformemente repartida en el plano del terreno produce presiones constantes iguales a:

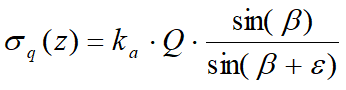
Integrando la tensión de la fórmula se obtiene el empuje total debido a la sobrecarga:

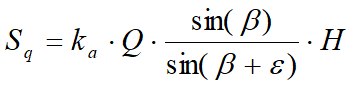
Con punto de aplicación en H/2 (siendo la distribución de tensiones constante). En las fórmulas anteriores:

 

b        = Inclinación de la  pared interna con respecto al plano horizontal pasante por la base

e        = Inclinación del plano del terreno con respecto al plano horizontal, positiva si es al contrario de las manecillas del reloj

Ka        = Coeficiente de presión activa calculado en el párrafo anterior

 

Franja de carga en plano terreno inclinado

La carga agente se descompone en una carga ortogonal y una tangencial al relleno, las presiones inducidas en la pared se calculan como se indica a continuación.

 

Franja de carga ortogonal al plano de acción

Una carga repartida de forma parcial con abscisa inicial x1 y abscisa final x2 genera un diagrama de presiones en la pared cuyos valores se determinan según la fórmula de Terzaghi, que expresa la presión en la genérica profundidad z como sigue:

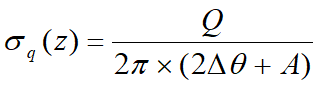
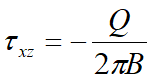
Con:

Dq=q1-q2;

 

A=sen(2q1)-sen(2q2)

 

B=cos(2q1)-cos(2q2)

 

q1=arctg(z/x1)

 

q2=arctg(z/x2)

 

Por integración se obtiene el resultado y el brazo relativo.

 

Franja de carga tangencial al plano del terreno

 

T        =        Intensidad de la carga  [F/L²]

D        =        4´log[senq1/senq2]

E        =        sen²q1-sen²q2

 

Líneas de carga sobre el relleno

Las líneas de carga generan un incremento de presiones en la pared que, según BOUSSINESQ, en la profundidad z, se puede expresar como:

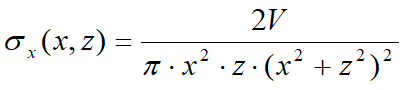
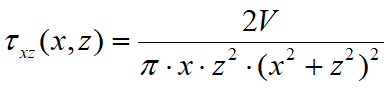
Donde:

V        =Intensidad de la carga en [F/L];

X        =        Distancia, en proyección horizontal, del punto de aplicación de la carga desde la pared

 

Si el plano de acción es inclinado e se rota el sistema de referencia de xz a XZ, con la siguiente transformación:

 

 

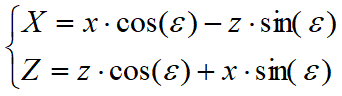
Empuje en presencia de  acuífero

El nivel freático con superficie distante Hw de la base de la estructura, induce presiones hidrostáticas normales en la pared que, en profundidad z, se expresan:

 

El empuje hidrostático total se obtiene por integración a lo largo de toda la altura relación precedente:

 

 

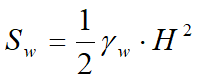
Indicando con H la altura total de empuje y con gw el peso específico del agua. El empuje del terreno sumergido se obtiene sustituyendo gt con g't (g't = gsaturo - gw), peso específico del material sumergido en agua. En condiciones sísmicas, el empuje que el agua produce se determina mediante la siguiente fórmula:

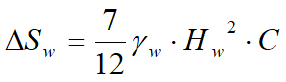
aplicada a 2/3 de la altura del nivel freático  Hw [Matsuo O'Hara (1960) Geotecnica , R. Lancellotta]

 

Efecto debido a la presencia de cohesión

La cohesión induce presiones negativas constantes iguales a:

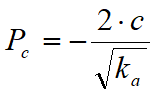
No siendo posible establecer a priori el decremento que produce el empuje por efecto de la cohesión,  se calcula la altura crítica Zc como a continuación:

 

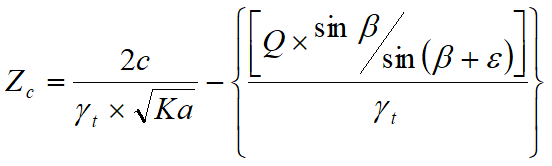
Donde:

Q        =        Carga agente sobre el relleno (si existe)

gt        = Peso específico del terreno

b        = Inclinación de la pared interna con respecto al plano horizontal pasante por la base

e        = Inclinación del plano del terreno con respecto al plano horizontal, positiva si es al contrario de las manecillas del reloj

C        = Cohesión del material

Ka        = Coeficiente de presión activa, calculado en los pasos anteriores

 

Si se da el caso de que la Zc calculada con la fórmula precedente es menor que cero, es posible sobreponer directamente los efectos de los diagramas, estableciendo un decremento en el diagrama de empuje original calculado como sigue:

Donde H es la altura total del empuje.

 

Sismo

Empuje activo en condiciones sísmicas

En presencia de sismo la fuerza de cálculo que ejerce el relleno sobre la pared está dada por:

Donde:

H        =         altura excavación

Kv        = coeficiente sísmico vertical

g        =         peso específico del terreno

K        =         coeficientes de empuje activo total (estático + dinámico) (véase Mononobe & Okabe)

Ews        =         empuje hidrostático del agua

Ewd        =         empuje hidrodinámico.

En suelos impermeables el empuje hidrodinámico Ewd = 0, pero se lleva a cabo una corrección en el cálculo del ángulo  b de la fórmula de  Mononobe & Okabe :

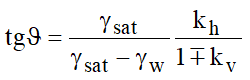
En suelos de alta permeabilidad, en condiciones dinámicas vale siempre la corrección anterior, pero  el empuje hidrodinámico asume la siguiente expresión:

Con H’ altura de nivel freático (de la sección del cálculo del  empuje hidrostático).

 

Resistencia pasiva

También para calcular la resistencia pasiva se pueden utilizar los dos métodos usados en el cálculo de la presión al estado límite activo (método de Coulomb y método de Caquot).

 

Método de Coulomb

En suelos homogéneos el diagrama de las presiones en condiciones de estado límite pasivo es linear con el siguiente tipo de ley:

De nuevo, integrando la relación anterior en la altura de empuje (la cual para las pantallas se debe estimar atentamente) se obtiene el empuje pasivo total:

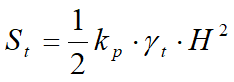
Donde H es la altura de empuje, gt el peso específico del terreno y kp el coeficiente de presión pasiva (en condiciones de estado límite pasivo). Este coeficiente se determina mediante la siguiente fórmula:

 

 

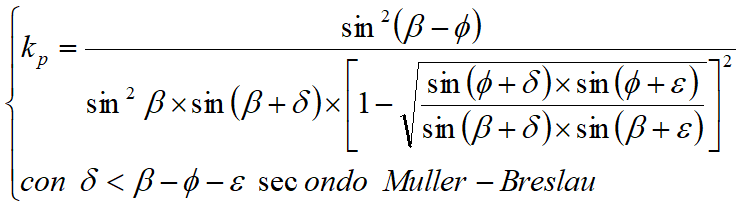
con valores límite  a:d< b-f-e (Muller-Breslau).

 

Método de  Caquot

El método de Caquot difiere del método de Coulomb por el cálculo del coeficiente de presión al estado límite pasivo. Con este método, el coeficiente de presión pasiva se calcula interpolando los valores de la siguiente tabla:

Tabella: Evaluación del coeficiente de presión pasiva con la teoría de Caquot

Carga uniforme sobre el relleno

La resistencia inducida por una carga uniformemente distribuida Sq vale:

 

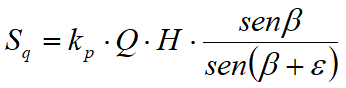
Con punto de aplicación H/2 (siendo el diagrama de las tensiones horizontales constante a lo largo de toda la altura). En la fórmula anterior, kp es el coeficiente de empuje pasivo calculado en el párrafo precedente.

 

Cohesión

La cohesión determina un incremento de resistencia igual a:

Tal incremento se suma directamente al diagrama principal de empuje.

 

Método del equilibrio límite (LEM)

El método del equilibrio límite consiste en la búsqueda de soluciones compatibles con el aspecto estático del problema (de comprobación o de proyecto). Básicamente se razona en términos del equilibrio de una estructura rígida, sin tener en cuenta la congruencia cinemática de los desplazamientos. Los principales esquemas de cálculo  a los cuales se hará referencia son los siguientes:

1.Pantalla en voladizo

2.Pantalla con un punto de sujeción, método de base libre

3.Pantalla con un punto de sujeción, método de base empotrada

Pantalla en voladizo: cálculo de la profundidad de empotramiento limite

En el caso de las pantallas en voladizo, la estabilidad está dada por la resistencia pasiva del terreno del intradós; del equilibrio de momentos respecto al centro de rotación se obtiene:

Donde:

Sm =        componente horizontal del empuje activo

Bm =        brazo de Sm respecto a O centro de rotación

Rv = componente horizontal de la resistencia pasiva

 

Bv   =        brazo de Rv respecto a O centro de rotación

Cada uno de estos términos está función de t, donde t es la profundidad del centro de rotación con respecto al plano del terreno del intradós.  La longitud necesaria para asegurar el equilibrio de traslación horizontal se obtiene aumentando t como a continuación:

 

Figura 2: Esquema de referencia para el cálculo del equilibrio de la pantalla

 

Coeficiente de seguridad resistencia pasiva

La longitud de empotramiento d anterior está relacionada con la condición límite de incipiente colapso, mediante un coeficiente F. Se puede introducir un margen de seguridad en las resistencias pasivas como a continuación:

 

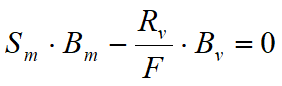
Pantalla con un punto de sujeción, método de base libre: Cálculo de la profundidad de empotramiento límite

La estabilidad de la obra está asegurada también con un punto de sujeción próximo a la coronación. Para utilizar el método de cálculo de base libre, la pantalla debe ser suficiente corta y rígida. La longitud de empotramiento se determina estableciendo el equilibrio de rotación al origen del anclaje indicado B1  

 

Donde:

Sm        = componente horizontal del empuje activo

H        = altura terreno a sostener

T        = profundidad de empotramiento calculada

Bm        =        brazo de Sm respecto a la base de la pantalla

Pm        = ordenada del punto de aplicación del anclaje en el trasdós

Rv        = componente horizontal de la resistencia pasiva

Bv        = brazo de Rv.

Conociendo t, se determinan Sm y Rv y el relativo esfuerzo del anclaje.

 

Coeficiente de seguridad F resistencias pasivas

La longitud de empotramiento se aumenta para tener más margen de seguridad en condiciones de servicio, usando el coeficiente de seguridad  F:

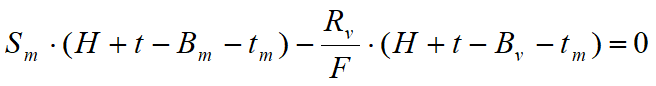
Pantalla con un punto de sujeción, método de base empotrada: Cálculo de la profundidad de empotramiento límite

Si la sección más profunda de la pantalla no se mueve y no gira, puede asimilarse a un empotramiento y en tal caso  se usa el método de la base empotrada. El procedimiento elaborado por Blum permite establecer la profundidad de empotramiento (t+t'), imponiendo condiciones cinemáticas de desplazamiento nulos en la base de la obra y en el origen del anclaje (B1) y las condiciones estáticas de momento y corte nulo en la base de la pantalla. Esto conduce a una ecuación de 5° grado en (t+t') que se puede resolver fácilmente.

 

Coeficiente de seguridad F resistencias

Para aumentar el factor de seguridad se han introducido valores de las resistencias pasivas reducidas.

 

Método de elementos finitos (FEM)

El método de elementos finitos (MEF) es el método que cuenta con más bases teóricas sólidas y racionales. De hecho, el método presupone que el problema se trate teniendo en cuenta ya sea el aspecto estático (y por lo tanto el equilibrio del problema) que el aspecto cinemático (y por lo tanto la congruencia de los desplazamientos y deformaciones).

Con el MEF la pantalla se modela como un conjunto de vigas (elementos beam), vinculadas en continuidad al terreno por medio de resortes elásticos cuyas rigidez se estima en función de las propiedades elásticas del terreno. En la siguiente figura se muestra el esquema del modelo utilizado para el análisis con elementos finitos:

 

 

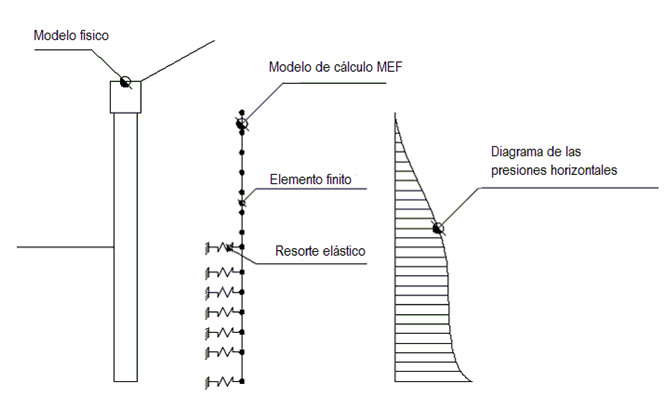
Figura 3: Esquema de la pantalla con elementos finitos

Con este método de cálculo es necesario conocer varios aspectos. Las principales partes que componen la aplicación del método son las siguientes:

Cálculo del módulo de reacción Ks del terreno

Como ya se ha mencionado, el suelo se modela con resortes de rigidez Ks aplicados en los nodos de los segmentos comprendidos entre el nodo de fondo excavación y la extremidad del empotramiento. La rigidez Ks se estima con base en la capacidad portante de las cimentaciones según la siguiente fórmula:

Donde:

As        =        constante, calculada como: As=C´(c´Nc+0.5´G´B´Ng)

Bs        =        coeficiente función de la profundidad Bs=C´G´Nq

Z        =        Profundidad examinada

C        =        40 en el sistema internacional SI

n        =        p´tanj

Nq        =        exp[n´(tan²(45° + j/2)]

Nc        =        (Nq-1)´cotj

Ng        =        1.5´(Nq-1)´tanj

Anclajes

Los anclajes se modelan como elementos elásticos, con sección transversal de área A, módulo de elasticidad  E y longitud L. En un tramo de pantalla de anchura unitaria, la acción de los anclajes inclinados de un ángulo b vale:

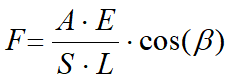
Sifonamiento

El sifonamiento es un fenómeno que en una fase inicial se localiza en la base de la pantalla, y después rápidamente se extiende al entorno del volumen resistente. Se da cuando, por una elevada presión hidrodinámica o de infiltración, se anulan las presiones pasivas eficaces, con la consecuente pérdida de resistencia del terreno. Se asume por norma un factor de seguridad Fsif=3.5-4  Indicando con:

ic = Gradiente hidráulico crítico

ie = Gradiente hidráulico en condiciones de ejercicio

El margen de seguridad se define como la relación entre ic y ie. Si ie<ic la pantalla es estable.

Comprobación de las secciones y cálculo de las armaduras

El cálculo de las armaduras y las comprobaciones presio-flexión y corte de la pantalla sometida a las solicitaciones N,M y T, se efectúan en la sección más solicitada. Las solicitaciones de cálculo se obtienen como producto entre las solicitaciones obtenidas con un cálculo a metro linear y el intereje entre pilotes (o el ancho de las pantallas continuas):

 

Donde: M', M', T' representan el momento, el corte y el esfuerzo normal relativos a una franja unitaria de cálculo mientras i es el intereje entre pilotes en caso de pantallas de pilotes o micropilotes (o el ancho de las pantallas continuas).

 

 

 

©    Geostru