Con il termine filtrazione si indica quel fenomeno fisico per il quale si verifica il passaggio dell' acqua da una zona con una data energia a un' altra zona con energia minore, attraverso un mezzo poroso. L' energia può essere espressa come somma dell' energia cinetica legata alla velocità del fluido, di quella potenziale dipendente dalla posizione del punto e di quella di pressione del liquido nello stesso punto. Dato che la velocità di filtrazione è sempre molto piccola il termine cinetico è trascurabile. Nello studiare la filtrazione dell' acqua si possono presentare problemi, sia di moto permanente che di moto vario. Con riferimento alla pressione dell' acqua, che gioca un ruolo importante nella maggior parte dei problemi di stabilità, si ricorda che in moto permanente essa rimane costante nel tempo, mentre in moto vario è funzione del tempo e quindi può crescere o diminuire con esso. Con riferimento alla quantità d' acqua che nel fenomeno di filtrazione attraversa una certa zona, si ricorda che in regime permanente la quantità d' acqua che entra è eguale a quella che esce, mentre in regime vario non vi è uguaglianza e la differenza rappresenta il volume d' acqua che viene accumulato o espulso dal terreno nell' intervallo di tempo considerato. Nel fenomeno della consolidazione, che è una particolare condizione di regime vario, entra in gioco anche la compressibilità del terreno. In regime permanente la zona di terreno nella quale si sviluppa la filtrazione, nello schema di rappresentazione che si adotta, ha due tipi di confini: uno è il luogo dove si conosce il carico d' acqua e si definisce confine o condizione limite del potenziale; l' altro è un contorno di materiali impermeabili, come roccia impermeabile, argilla, ecc. che delimita lo strato in cui avviene la filtrazione e si definisce quindi confine o condizione limite del flusso d'acqua. Per precisare quanto detto basta ricordare ad esempio le condizioni di flusso dell'acqua nella prova di permeabilità a carico costante. In questa prova evidentemente i confini del potenziale sono le superfici di entrata e di uscita dell'acqua dal campione di terra. Poiché le pareti del contenitore sono impermeabili il flusso è parallelo al contenitore e la parete costituisce il confine del flusso d'acqua:
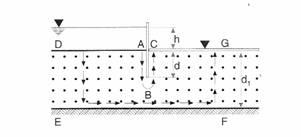
Schema relativo al flusso d'acqua
Un caso pratico è costituito dalla palancolata (figura precedente) che sostiene un livello costante h di acqua e che è infissa nel terreno fino alla profondità d in uno strato omogeneo di terreno permeabile (sabbia o ghiaia) di spessore dI, che appoggia su uno strato impermeabile (roccia o argilla). In questo caso si ha un moto confinato, poiché le condizioni al contorno della regione in cui avviene il moto sono geometricamente definite. Il flusso dell'acqua è causato dal carico idraulico h; sulla superficie AD agisce un carico costante e questa superficie costituisce il primo confine del potenziale nel nostro problema; anche su CG il carico è costante e questa superficie costituisce il secondo confine. Ovviamente per assolvere i suoi compiti la palancolata deve essere impermeabile, quindi la sua superficie ABC costituisce uno dei confini del flusso mentre la superficie EF dello strato impermeabile costituirà l'altro confine. Ovviamente in linea teorica se le caratteristiche dell'acqua, del terreno e dello strato impermeabile, a monte e a valle della palancolata, si mantengono costanti si può considerare che i punti D, E, F e G siano all'infinito; in pratica generalmente si considera che la lunghezza interessata sia compresa entro 4-5 volte lo spessore dello strato. Per determinare la quantità d'acqua che filtra nel terreno si fanno le ipotesi che il flusso dell'acqua sia retto dalla legge di Darcy e che il terreno sia omogeneo, isotropo e incompressibile:
![]()
Si ricordi che la legge di Darcy è valida per moto laminare, condizione che si verifica per certi valori del numero di Reynolds, R. Il valore di R, che caratterizza il passaggio da moto laminare a turbolento, assume valore diverso a seconda degli autori; Taylor (1948) ha indicato come criterio di validità per la legge di Darcy R <= 1. Altri ricercatori hanno esaminato, specialmente per le argille, il collegamento tra le condizioni di moto e il gradiente idraulico; in particolare Tavenas e altri (1983) sono arrivati alla conclusione che, per quanto riguarda le argille, la legge di Darcy è valida per gradienti compresi tra 0,1 e 50. Per calcolare la portata di filtrazione attraverso i terreni è utile determinare la distribuzione della pressione dell' acqua dei pori mediante la costruzione del reticolato di flusso, cioè del sistema di linee di corrente e di linee equipotenziali che rappresentano il flusso dell' acqua attraverso un terreno incompressibile. Accettando l’ipotesi di terreno incompressibile per i moti di filtrazione in regime permanente e piani l’equazione di continuità può essere scritta nella forma:
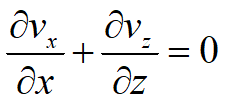
Le due componenti della velocità del liquido, in base alla legge di Darcy possono essere espresse nella forma:
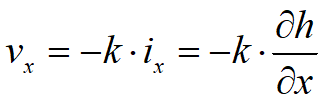
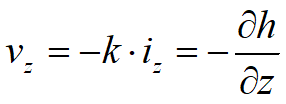
Unendo queste tre equazioni si ottiene:
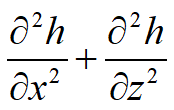
che è l’equazione di Laplace per moto permanente su un piano, nell’ipotesi di materiale omogeneo, isotropo e incompressibile. Questa equazione può essere espressa a mezzo di due funzioni coniugate φ e ψ. Possiamo infatti esprimere le componenti di velocità come derivate parziali rispetto ad x e z della funzione φ = k h e quindi:
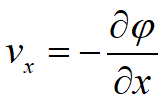
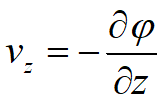
Allora possiamo anche scrivere:
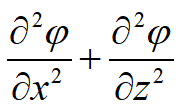
L'esistenza della funzione φ = k h, funzione a potenziale di velocità per un fluido in moto, implica vorticità nulla e che il moto sia irrotazionale. Possiamo allora dire che si ha una funzione di corrente tale che:
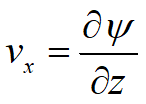
E quindi si ha:
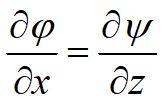
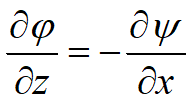
E possiamo anche scrivere
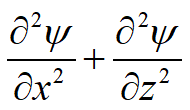
φ e ψ sono conosciute rispettivamente come funzione di potenziale e funzione di corrente. Riprendendo ora il caso, prima indicato, dell'acqua che filtra attraverso il terreno al di sotto di una palancolata (figura seguente) si ha che due linee equipotenziali sono le superfici del terreno a monte e a valle della stessa palancolata; inoltre la superficie dello strato impermeabile è una linea di corrente o di flusso. Risolvendo l'equazione di Laplace in accordo con queste condizioni limite, possiamo costruire la rete di flusso. Ogni striscia compresa tra due linee di flusso adiacenti è un canale di flusso ed ogni parte del canale di flusso compresa tra due linee equipotenziali è un campo. È pertanto conveniente costruire le linee equipotenziali in maniera che il dislivello piezometrico tra due linee successive sia costante e le linee di flusso in modo tale che ogni canale di flusso abbia una portata costante. Se h è il carico idraulico totale e Na è il numero di dislivelli piezometrici individuati, la differenza di carico idraulico tra due linee equipotenziali successive è:
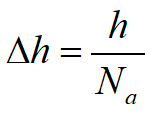
In un punto z come indicato nella seguente figura la pressione vale:
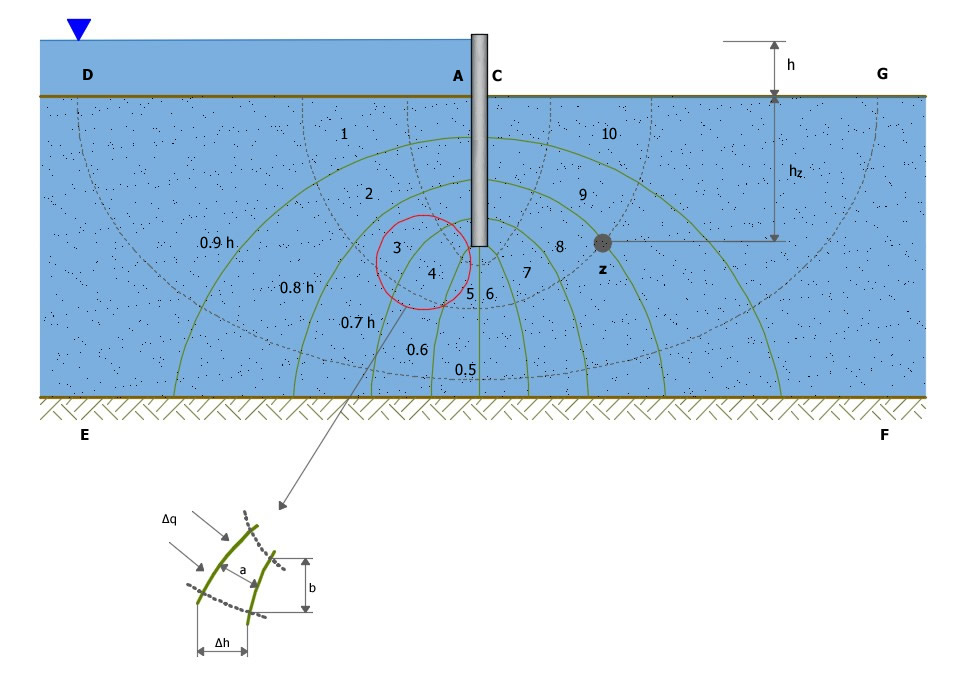
Schematizzazione del reticolo di flusso
essendo n il numero di dislivèlli piezometrici attraversati per giungere In z. Nell'esempio relativo alla figura precedente si ha:
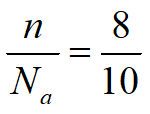
Se non ci fosse alcun flusso d'acqua, cioè se la superficie a valle fosse impermeabile, la pressione idrostatica in questo punto varrebbe:
![]()
poiché l'acqua si muove, si ha una perdita di carico che secondo la rete di filtrazione disegnata nel punto z è pari a 8/10h. La sovrappressione dell'acqua nel punto z è data quindi da:
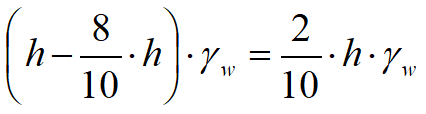
Per conoscere la portata di filtrazione consideriamo un campo, cioè un'area compresa fra due linee di flusso e due linee equipotenziali; la lunghezza del lato nella direzione delle linee di flusso è a e quindi il gradiente idraulico in un campo è:
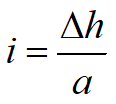
e la velocità:
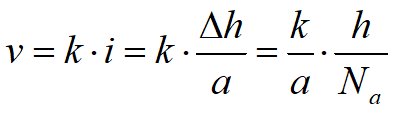
Poniamo che l'altro lato del campo sia di lunghezza b allora la portata attraverso il campo per unità di lunghezza di palancolata sarà:
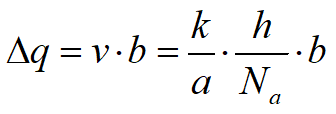
per ogni tubo di flusso; se si pone b = a, cioè se gli elementi della rete di filtrazione sono quadrati, si ottiene:
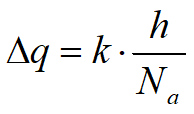
Se Nb è il numero totale di canali di flusso la portata totale per unità di lunghezza di palancolata sarà:
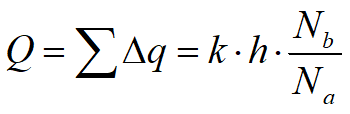
In questo modo, quando si sia costruita la rete di flusso, si può calcolare facilmente la portata. La rete di filtrazione viene spesso costruita con metodi sperimentali in laboratorio, con modelli analogici o graficamente per tentativi. In situazioni complesse del sottosuolo, per successione di strati e per anisotropia della permeabilità, si può ottenere la rete di filtrazione per mezzo di metodi numerici (FEM, BEM, metodo delle differenze finite).
© GeoStru