The finite-elements method is the method which is based more than any other one upon solid and rational theoretical bases. The method presupposes that the problem is faced taking into account both the static aspect (and consequently the equilibrium of the problem) and the kinematic aspect (and consequently the congruence of the displacements or rather of the deformations). In the FEM method, the bulkhead is modeled like a set of beams (beam elements), with continuity bound to the ground by means of elastic springs, whose stiffness is estimated according to the elastic properties of the ground. In the following figure is schematically shown the model used for the analysis with finite-elements:
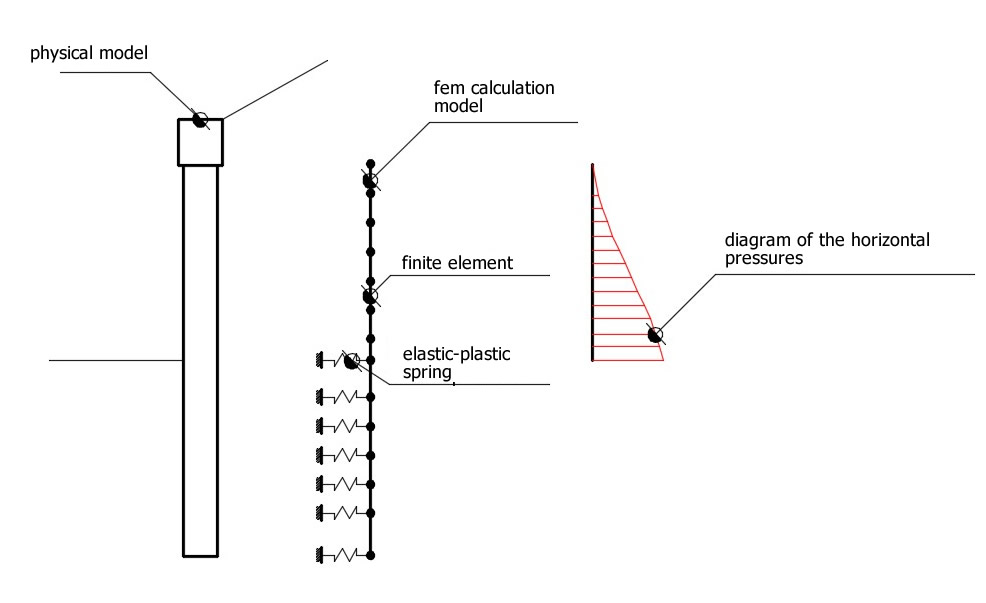
Schematization of the bulkhead-ground complex by means of finite-elements
The finite-elements method requires the knowledge of the ground and structure properties (unlike the LEM method, in which a condition of equilibrium for the rigid body is imposed). In particular, it is necessary to know the modulus of subgrade reaction of the ground. The main parts composing the application of the method are the following:
•Characterization of the structure materials by means of:
- evaluation of the active and passive thrust coefficients as well as of the modulus of subgrade reaction for the ground
- evaluation of the flexural stiffness – shearing and normal – of the bulkhead
•Discretization of the bulkhead in finite elements and modeling of the springs:
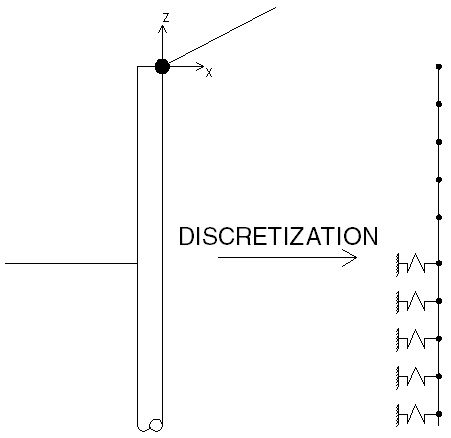
Discretization procedure
•Assembly of the contributions of each finite element
In this phase, the problem is reported in global, assembling the stiffness contributions of each finite element.
•Solution of the problem
The problem with finite elements is posed in terms of non-linear system in displacement variables. In this phase, an iterative procedure is set so as to allow the solution to a non-linear problem of the following kind:
![]()
In the previous equation, K(u) is the stiffness matrix of the problem (non-linear type), u is the displacement field that is the solution of the problem, and p is the vector of the external loads (associated to the distribution of ground pressures).
•Assembly and interpretation of the solution
Once the values of the u vector components have been determined, all information (relevant to the structural analysis) can be derived. In particular, the following parameters will be determined:
oMoment
oShear
oNormal stress
© GeoStru